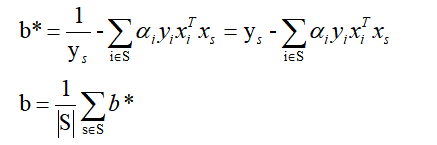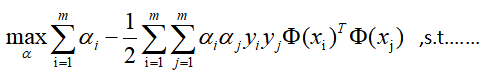ML-支持向量:SVM、SVC、SVR、SMO原理推导及实现
目录
1.导出目标
2拉格朗日转换
3对偶问题:
4求对偶问题
5 求b
6 得出模型
6.1 f(x)的约束条件:
7 核函数
7.1 软间隔
7.2 松弛变量:
7.3 KKT约束
8 SMO求a
8.1对偶问题上,上面已知对偶形式:
8.2.SMO算法思想
8.2.1更新方法
8.2.2 推导过程
8.2.3选两点a1,a2的方法
8.2.4b和E计算更新
8.3算法伪代码
8.4完整实现:
python版
9 SVR支持向量回归
10 sklearn实现SVC(支持向量分类),SVR(支持向量回归):
1)分类classification
2)回归Regression
附一个SVC的实现:
1.导出目标
2拉格朗日转换
3对偶问题:
因为是希望得出L最小时的一些参数w,b,a,但是目前很难一起求得最佳参数,所以换个思路。因为:
所以能够容易的计算出拉格朗日乘子a约束时的最坏情况是:
但是m个a的值还是无法求出,而后面会得知,根据L对w,b的求导关系,w,b可以被a表示出来,所以关键变为求a。
根据对偶关系,极大值关系可以转为极小值关系,且转换后的问题会不大于原问题,在取得极值的时候才取等号,也就是:
这样问题变为,先把w,b求导关系代入求L极小值关系,最后再寻找a的问题,最后a的求解会通过SMO等思路求解,具体SMO放到最后讲解,因为太难了。
4求对偶问题
1)求L的极小值时的w,b,求导:
得出极小值需满足如上这些关系
2)代入L求导关系式,求关于a的极大值:
所以关键是对这个函数求极大值时的a,假设通过后面的SMO找到了,记为a*,那么显然得到了w的解析式:
5 求b
因为对于所有支持向量点(正例上支持向量点位于WTx+b = 1超平面上,反例WTx+b= -1)记作(xs,ys),均有:
根据KKT条件:ai>0时,yi(WTxi+b)-1=0:(必定:WTxi+b = 1 或WTxi+b= -1)即xi必须是支持向量点,而ai=0时:
也就是说对w无影响,因此上式中w还可以简化成只考虑支持向量点计算(实际上这就是SVM称为支持向量机的原因,因为模型真正起作用的,就只是这些支持向量点):
假设我们有S个支持向量(位于WTx+b = 1,WTx+b= -1超平面上的点集),则对应我们求出S个b∗,理论上这些b∗都可以作为最终的结果, 但是我们一般采用一种更健壮的办法,即求出所有支持向量所对应的b∗,然后将其平均值作为最后的结果:
6 得出模型
ai参数求出之后,如上所示,就相当于求出了w,b了。就可以得到模型,进行预测了:
def _f(self, i):
r = self.b
for j in range(self.m):
r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])
return r
6.1 f(x)的约束条件:
7 核函数
现实中可能有些不存在线性的可分超平面,但是可能映射到更高维度可能就可分了,有证明显示,如果原始空间维度有限,那么一定存在高维特征空间使样本可分。
这样对x的映射关系,可以直接用到上面推导的所有公式里:
原问题映射:
对偶形式映射:
这种映射我们并不知道具体是如何的,因此也不知如何去计算了,所以这里就设想出来核函数的概念了:
def kernel(self, x1, x2):
if self._kernel == 'linear':
return sum([x1[k] * x2[k] for k in range(self.n)])
elif self._kernel == 'poly':
return (sum([x1[k] * x2[k] for k in range(self.n)]) + 1) ** 2
return 0假设出原来的这种内积映射,是等价于某个函数k(.,.)计算的结果。问题就变成了:
求解后模型为:
核函数性质
k是核函数,当且仅当’核矩阵’K总是半正定:
常见核函数列表:
另外核函数线性组合起来还是核函数(系数为正),k1,k1,r1>0,r2>0:k3=r1k1+r2k2 也是核函数
7.1 软间隔
讨论软间隔是因为像这种情况,严格分出来(线性不可分了已经,用核函数可以分)是个弯曲的,但实际上应该就是这下面这样一条斜线才是最好的模型表示:
因此办法是,允许在一些情况下出现错误,引入软间隔的概念,在这个软间隔内允许出错。也就是允许不满足约束:
对于不满足的点,我们会累记一个损失函数,再引入惩罚力度因子C,则可以重新定义优化目标:
7.2 松弛变量:
显然,这些损失是常数且>=0,因此引入松弛变量的概念替换原来的损害函数计算结果,重写简化:
上式进行拉格朗日变换:为什么这样:https://blog.csdn.net/jiang425776024/article/details/87607526
同样的求导,对偶和上面4一致,省略。最终得到如下对偶问题:
7.3 KKT约束
可见,与非软间隔的问题相比,仅仅是对约束ai多了一个上界约束,且约束就是<惩罚因子C。然后同样SMO解得参数就可以得到模型f(x)了,和6一致,同样因为存在不等式约束约束,所以这里模型f(x)有KKT条件约束:
这个约束是有道理的:
a) 如果α=0,那么yi(wTxi+b)−1≥0,即样本在间隔边界上或者已经被正确分类。
b) 如果0<α c) 如果α=C,说明这是一个可能比较异常的点,需要检查此时ξi 1)如果0≤ξi≤1,那么点被正确分类,但是却在超平面和自己类别的间隔边界之间 2)如果ξi=1,那么点在分离超平面上,无法被正确分类。 3)如果ξi>1,那么点在超平面的另一侧,也就是说,这个点不能被正常分类 实现代码,判断是否否后KKT条件,True符合,False不符合: 在SMO算法中的思想是,每次选择一对变量(αi,αj)进行优化,其余m-2个固定看作是常量, 因为在SVM中,α并不是完全独立的,而是具有约束的: 因此一个只选一个ai,那么ai可以被其它表示。 假设我们选取的两个需要优化的参数为α1,α2, 剩下的α3,α4,…,αm则固定作为常数处理。将SVM优化问题进行展开就可以得到(把与α1,α2无关的项合并成常数项C):(省略了a3+a4+...+am=C,因为其对max函数无意义) 因为y1,y2只能是1/-1,因此a1,a2的关系被限制在盒子里的一条线段上(只能是a1-a2/a1+a2两种情况),所以两变量的优化问题实际上仅仅是一个变量的优化问题(一个能由另一个得出)。我们假设是对a2的优化问题,所以只存在2幅图的情况: 1)y1!=y2,则约束a1y1+a2y2=k:a1-a2=k,L,H为约束下a2的最小最大值,为下图 2)y1=y2: 则最优化问题转为更新: 最终更新方式: 剪辑判断: a1,a2更新: 则: 求导: 代入关系式,添加新旧标记方便迭代更新: 得: 得出上面的更新方式。 SMO每个子问题选择两个变量优化,其中至少一个变量是违法KKT条件的。 第1个变量a1的选择 SMO称选择第一个变量的过程为外层循环,外层循环选取违反KKT条件最严重的样本点(xi,yi)对应的ai值作为第一个变量a1;检测是否满足KKT条件(7.3有具体介绍): 一般,外层循环先遍历所有满足0 第2个变量a2的选择 SMO算法称选择第二一个变量为内层循环,假设我们在外层循环已经找到了α1, 第二个变量α2的选择标准是让|E1−E2|有足够大的变化。8.2.1定义了E(预测值与真实值之差)。由于α1定了的时候,E1也确定了,所以要想|E1−E2|最大,只需要在E1为正时,选择最小的Ei作为E2,在E1为负时,选择最大的Ei作为E2,可以将所有的Ei保存为列表,加快迭代。 如果内存循环找到的点不能让目标函数有足够的下降,可以采用遍历支持向量点来做α2,直到目标函数有足够的下降, 如果所有的支持向量做α2都不能让目标函数有足够的下降,可以跳出循环,重新选择α1。 构建一个宽度为2ε的间隔带,若训练样本落入此间隔带,则认为是被预测正确的。图像: 和SVM类似的,因此SVR问题可转化为: 其中L是误差计算函数,对小于epsilon的误差为0: 同样是数字,引入松弛变量替代,(间隔带两侧的松弛程度可有所不同),则变成: 约束(即预测值与真实的差<=epsilon+松弛变量): 引入拉格朗日乘子,可得拉格朗日函数: 存在不等式约束,所以上式还有KKT条件等约束。同样的求导,然后对偶。 求导: 把上边的式子带入,即可求得SVR的对偶问题: KKT条件: 如果求出a的话最后,可得SVR的模型: scikit-learn SVM算法库封装了libsvm 和 liblinear 的实现,仅仅重写了算法了接口部分。分为两类,分类:SVC, NuSVC,和LinearSVC。回归:SVR, NuSVR,和LinearSVR 。相关的类都包裹在sklearn.svm模块中。sklearn官方svm API:https://scikit-learn.org/stable/modules/classes.html#module-sklearn.svm。 SVC, NuSVC,和LinearSVC。SVC, NuSVC类似,区间是NuSVC多了nu参数: 因此nu没有惩罚系数C,因为它会自己选: LinearSVC从名字就可以看出,是线性分类,也就是不支持各种低维到高维的核函数,仅仅支持线性核函数,对线性不可分的数据不能使用。 SVR, NuSVR,和LinearSVR。SVR, NuSVR差不多,区别仅仅在于对损失的度量方式不同,NuSVR有nu参数: 1)一般推荐在做训练之前对数据进行归一化,当然测试集中的数据也需要归一化。。 2)在特征数非常多的情况下,或者样本数远小于特征数的时候,使用线性核,效果已经很好,并且只需要选择惩罚系数C即可。 3)在选择核函数时,如果线性拟合不好,一般推荐使用默认的高斯核'rbf'。这时我们主要需要对惩罚系数C和核函数参数γγ进行艰苦的调参,通过多轮的交叉验证选择合适的惩罚系数C和核函数参数γγ。 4)理论上高斯核不会比线性核差,但是这个理论却建立在要花费更多的时间来调参上。所以实际上能用线性核解决问题我们尽量使用线性核。 这个有个不错的中文表格介绍参数:https://www.cnblogs.com/pinard/p/6117515.html 使用方法具体看官方例子: LinearSVC:https://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVC.html#sklearn.svm.LinearSVC LinearSVR :https://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVR.html#sklearn.svm.LinearSVR NuSVC:https://scikit-learn.org/stable/modules/generated/sklearn.svm.NuSVC.html#sklearn.svm.NuSVC NuSVR:https://scikit-learn.org/stable/modules/generated/sklearn.svm.NuSVR.html#sklearn.svm.NuSVR SVC:https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC SVR:https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html#sklearn.svm.SVR 可视化:https://blog.csdn.net/jiang425776024/article/details/87857059 def _KKT(self, i):
y_g = self._g(i) * self.Y[i]
if self.alpha[i] == 0:#a=0:需要yif(xi)-1>=0
return y_g >= 1
elif 0 < self.alpha[i] < self.C: #0
8 SMO求a
8.1对偶问题上,上面已知对偶形式:
8.2.SMO算法思想
8.2.1更新方法
if self.Y[i1] == self.Y[i2]:
L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
H = min(self.C, self.alpha[i1] + self.alpha[i2])
else:
L = max(0, self.alpha[i2] - self.alpha[i1])
H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])def _E(self, i):
return self._f(i) - self.Y[i] def _compare(self, _alpha, L, H):
# 剪辑操作
if _alpha > H:
return H
elif _alpha < L:
return L
else:
return _alpha # 边界
if self.Y[i1] == self.Y[i2]:
L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
H = min(self.C, self.alpha[i1] + self.alpha[i2])
else:
L = max(0, self.alpha[i2] - self.alpha[i1])
H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])
E1 = self.E[i1]
E2 = self.E[i2]
eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2], self.X[i2]) - 2 * self.kernel(
self.X[i1], self.X[i2])
if eta <= 0:
# print('eta <= 0')
continue
alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E1 - E2) / eta
alpha2_new = self._compare(alpha2_new_unc, L, H)
alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)
self.alpha[i1] = alpha1_new
self.alpha[i2] = alpha2_new 8.2.2 推导过程
8.2.3选两点a1,a2的方法
def _init_alpha(self):
# 外层循环首先遍历所有满足08.2.4b和E计算更新
b1_new= self.b
b2_new= self.b
if 0 < alpha1_new < self.C:
b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1])
* (alpha1_new - self.alpha[i1]) - self.Y[i2]
* self.kernel(self.X[i2], self.X[i1])
* (alpha2_new - self.alpha[i2])
+ self.b
if 0 < alpha2_new < self.C:
b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2])
* (alpha1_new - self.alpha[i1]) - self.Y[i2]
* self.kernel(self.X[i2], self.X[i2])
* (alpha2_new - self.alpha[i2])
+ self.b
b_new = (b1_new + b2_new) / 2
self.b = b_new
# 更新E
self.E[i1] = self._E(i1)
self.E[i2] = self._E(i2)8.3算法伪代码
8.4完整实现:
python版
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
for i in range(len(data)):
if data[i, -1] == 0:
data[i, -1] = -1
# print(data)
return data[:, :2], data[:, -1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
class SVM:
def __init__(self, max_iter=100, kernel='linear'):
self.max_iter = max_iter
self._kernel = kernel
def init_args(self, features, labels):
self.m, self.n = features.shape
self.X = features
self.Y = labels
self.b = 0.0
# 将Ei保存在一个列表里
self.alpha = np.ones(self.m)
self.E = [self._E(i) for i in range(self.m)]
# 松弛变量
self.C = 1.0
def _KKT(self, i):
y_g = self._g(i) * self.Y[i]
if self.alpha[i] == 0:
return y_g >= 1
elif 0 < self.alpha[i] < self.C:
return y_g == 1
else:
return y_g <= 1
# g(x)预测值,输入xi(X[i])
def _g(self, i):
r = self.b
for j in range(self.m):
r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])
return r
# 核函数
def kernel(self, x1, x2):
if self._kernel == 'linear':
return sum([x1[k] * x2[k] for k in range(self.n)])
elif self._kernel == 'poly':
return (sum([x1[k] * x2[k] for k in range(self.n)]) + 1) ** 2
return 0
# E(x)为g(x)对输入x的预测值和y的差
def _E(self, i):
return self._g(i) - self.Y[i]
def _init_alpha(self):
# 外层循环首先遍历所有满足0
9 SVR支持向量回归
10 sklearn实现SVC(支持向量分类),SVR(支持向量回归):
1)分类classification
nu
LinearSVC 和SVC没有这个参数,LinearSVC 和SVC使用惩罚系数C来控制惩罚力度。
nu代表训练集训练的错误率的上限,或者说支持向量的百分比下限,取值范围为(0,1],默认是0.5.它和惩罚系数C类似,都可以控制惩罚的力度。
惩罚系数C
即为我们第二节中SVM分类模型原型形式和对偶形式中的惩罚系数C,默认为1,一般需要通过交叉验证来选择一个合适的C。一般来说,如果噪音点较多时,C需要小一些。
NuSVC没有这个参数, 它通过另一个参数nu来控制训练集训练的错误率,等价于选择了一个C,让训练集训练后满足一个确定的错误率
2)回归Regression
nu
LinearSVR 和SVR没有这个参数,用ϵ控制错误率
nu代表训练集训练的错误率的上限,或者说支持向量的百分比下限,取值范围为(0,1],默认是0.5.通过选择不同的错误率可以得到不同的距离误差ϵ。也就是说这里的nu的使用和LinearSVR 和SVR的ϵ参数等价。
附一个SVC的实现:
from sklearn.svm import SVC
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
for i in range(len(data)):
if data[i, -1] == 0:
data[i, -1] = -1
# print(data)
return data[:, :2], data[:, -1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
clf = SVC()
clf.fit(X_train, y_train)
print('分数:', clf.score(X_test, y_test))
#分数: 0.96