机器学习(7)——支持向量机（一）：从感知机到线性可分支持向量机

前言

支持向量机(support vector machine)本来是最早接触的机器学习算法，最初自己写的的机器视觉论文也用到了SVM，但和神经网络一样，一直觉得它是比较复杂的机器学习方法，需要深入的学习和研究。因此先是系统推导了李航的《机器学习》，之后学习Andrew Ng的机器学习课程，并看了july、pluskid等人的技术博客。也不能说自己完全懂了，只能算是学习笔记，总结一些自己能掌握的东西。
我在接触SVM之初，深度学习已经比较火了，之所以还是运用SVM，一方面是因为SVM本身是现成比较成熟的分类算法，另一方面是之前很多论文都说了SVM的可靠性，在各方面表现都不错，而且有很多现成的资源（代表性有台湾林智仁团队的libsvm、liblinear）。为了快速应用机器学习，就选择了SVM。最终发现里面真的是博大精深，包含有太多不同的模型，涉及了大量的数学知识，而且至今仍是很多科研人员的研究方向。

感知机（回顾）

在之前总结感知机(perceptron)时介绍了感知机是神经网络(Neural Networks)和支持向量机(support vector machine, SVM)的基础。首先，我们来看感知机由输入空间到输出空间的映射函数，这与支持向量机是一样的：

f(x)=sign(wT⋅x+b)

其中sign函数的定义为：

sign(x)={+1,−1,x≥0x<0

当 wT⋅x+b≥0 时， f(x)=1 ；而当 wT⋅x+b<0 时， f(x)=−1 。
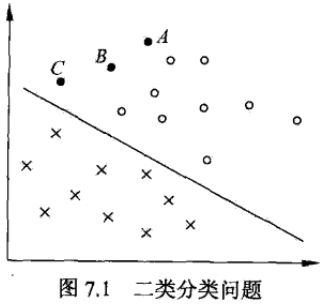
现在我们假设有如下图所示的两组数据，红色表示正样本+1，绿色表示负样本-1，点所在位置为样本特征值 x 。对于二分类问题就是找到如图所示的一条直线（高维对应超平面）能够准确将两类样本进行分类。
对于上面定义的感知机，正样本(红点)在直线上面，则 wT⋅x+b≥0 ，对应感知机输出结果 f(x)=1 ，即分类为正样本。同理，当样本点在直线下面时， wT⋅x+b<0 ，对应感知机输出结果 f(x)=−1 ，即负样本。由此我们可以看出，在二维平面的直线 wT⋅x+b=0 就能够将图中的正负样本正确分类。

当样本被错误分类时，样本真实类别 yi 与 wT⋅x+b 总是异号，则对错分样本 yi(wT⋅x+b)<0 。因此对于感知机来说，定义的损失函数为：

L(w,b)=−∑(xi,yi)∈Myi(wT⋅x+b)

其中M是错分样本集合，即样本被错分之后就有一定的损失代价。分类器的最终目的也就转为求解使代价函数最小的分类边界，在感知机中，只要求出使所有样本都正确分类的超平面，则损失函数代价就为0。
考虑到上图所示的二分类问题，感知机最终的目的只是将两类样本正确分类，我们可以看出是有多条直线满足该条件的，那么到底哪条才是 最恰当的分类界限呢？这是感知机无法解决的问题。
从几何直观上来看，就上图的二分类的问题 ，最佳决策边界应该是图中最近的红点和黑点连线的中垂线（黑色圈中的两个点），也就是说最佳决策边界主要 由最难分的两个样本点决定。这从感性上也比较好理解，因为对于难分离的样本，决策边界稍微转动一个角度，则有一个样本就可能被错分，即该样本很大程度影响了决策边界的分布，反之，离得较远的样本点则不会有影响。这就是支持向量机中支持向量的直观概念，下面我们先具体介绍线性可分支持向量机的一些知识。

线性可分支持向量机

通过上述介绍我们知道，感知机能够对线性可分样本进行正确分类，但是求得的分类超平面有很多，即决策边界不一定是最优的。通过线性可分支持向量机利用间隔最大化求最优分离超平面，这时决策边界是唯一的。
首先，通过下图我们可以看出，A点离分类平面较远，预测为正样本的确信度很高，C点离分类平面较近，预测为正样本的确信度较低。由此，我们可以看出样本分类的可信度可以通过样本点到分类边界的距离来定义。其中，相对距离可以由 |wT⋅x+b| 给出，则 y(wT⋅x+b) 可以用来表示分类的正确性(同号则分类正确，乘积大于0)及确信度(值越大表示离边界越远，可信度越高)。

因此，我们定义样本点 (xi,yi) 到超平面的函数间隔(functional margin)：

γi^=yi(wT⋅xi+b)=yif(xi)

而训练集 T 的 函数间隔为所有样本点中离超平面最近的点到超平面的函数间隔，即：

γ^=mini=1,2,…,Nγi^

γ^ 可以表示分类预测的正确性和确信度，因此可以通过最大化函数集 T 的函数间隔来增加分类的确信度。但是选择最佳超平面时，仅有函数间隔还不够，因为 当权重 w 和偏置 b 成倍改变时，超平面没有变化，但是函数间隔却改变了，并不能通过函数间隔简单确定最佳的分类超平面。此时我们定义 几何间隔来解决这个矛盾。
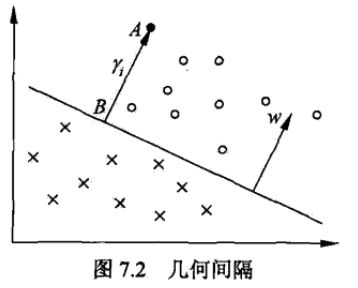
如下图所示，易证明：

xi−x0γi=w||w||

则 x0=xi−γiw||w|| ,而 x0 是 xi 投影在超平面上的点，满足 f(x0)=0 ，则：

f(x0)=wT(xi−γiw||w||)+b=0⟹γi=wT⋅xi+b||w||=f(xi)||w||

不过这里的 γi 是带符号的，我们需要的只是它的绝对值，由此我们可以推导出 几何间隔(geometrical margin)的定义为：

γi~=yiγi=γi^||w||

与函数间隔一样，样本集 T 到超平面的集合间隔为：

γ~=mini=1,2,…,Nγi~

支持向量机学习的基本思想就是求解能够正确划分样本集并且是几何间隔最大的分离超平面，简单来说就是求解区分度最大的超平面，即确信度最大的超平面。因此我们定义目标函数为：

maxw,bγ~

但却要满足一定的限制条件，即样本点到超平面的间隔至少都是 γ~ ：

s.t.yi(wT⋅xi+b||w||)≥γ~,i=1,2,…,N

又因为 γ~=γ^||w|| ,我们可以将优化问题改下为：

maxw,bs.t.γ^||w||yi(wT⋅xi+b)≥γ^,i=1,2,…,N

根据上面讨论我们知道，函数间隔 γ^ 并不影响最优化问题解，因为当权重 w 和偏置 b 成倍改变时，函数间隔也会成倍改变，而此时超平面并没有改变。因此可以通过固定其中一个值，来优化最终的结果。因为目标函数和约束条件中都带有 γ^ , 我们选择固定 γ^ 。 令 γ^=1 ，且最大化 1||w|| 与最小化 12||w||2 （1/2为调节系数，方便与优化计算）的效果是等价的。则我们的目标函数可以转换为：

minw,bs.t.12||w||2yi(wT⋅xi+b)≥1,i=1,2,…,N

通过求解这个最优化问题，我们就能够得到最大间隔的分类超平面。如下图所示：

因为我们前面固定最大函数间隔 γ^=1 ，则在支持超平面上的点满足：

H1:wT⋅xi+b=1(正例)H1:wT⋅xi+b=−1(负例)

在 H1 和 H2 上的点就是 支持向量。注意到 H1 和 H2 平行，且他们是间隔边界，他们之间没有样本点。在决定分类超平面时只有这些支持向量其作用，而其他样本点并不起作用。也就是说如果改变这些支持向量点，分类超平面可能会改变，而改变甚至移除非支持向量点，分类超平面是不会改变的。正是因为支持向量在确定分离超平面中起着决定性的作用，所以这种模型称为支持向量机。支持向量实际就是那些比较难以区分的样例，支持向量机的目的就是使这些难以区分的样例有最大的分类置信度。

PS：本处给出了线性可分支持向量机的一些基本概念和直观认识，通过与感知机对比直观上还是比较容易理解。难点在于目标函数的优化、线性不可分支持向量机以及非线性支持向量机的理解，将在后续笔记中进行介绍。