POJ1966 Cable TV Network

一.原题链接：http://poj.org/problem?id=1966

二.题目大意：给你一个很裸的网络，让你判断最少去掉多少个点能够使其不连通。注意是无向图。

三.思路：枚举每个源点和汇点，求每次的最小割点集。取一个最小的，如果是完全图，每次求出的网络流肯定是INF，此时没有割点集，题目要求输出顶点数。

注意要枚举每个源点和汇点，不能固定源点，因为源点有可能是割点，题目测试数据有问题：

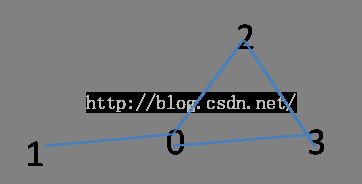
比如下图：

如果0为源点，跑最大流，出来的结果是INF，然而其实0就是那个最小割的点。

最小割点集合不懂建图的：详情请看http://blog.csdn.net/h992109898/article/details/51232440

四.代码：

#include 
#include 
#include 
#include 
#include 

using namespace std;

const int INF = 0x3f3f3f3f,
          MAX_N = 55;

class Dinic
{
public:
    struct Edge
    {
        int v, w, next;
    };

    int cnt, head[MAX_N*2], dist[MAX_N*2], s, t;
    Edge edges[MAX_N*MAX_N*2];

    void init(int is, int it)
    {
        cnt = 0;
        s = is, t = it;
        memset(head, -1, sizeof(head));
    }

    void addEdge(int u, int v, int weight)
    {
        edges[cnt] = (Edge){v, weight, head[u]};
        head[u] = cnt++;
        edges[cnt] = (Edge){u, 0, head[v]};
        head[v] = cnt++;
    }

    bool BFS()
    {
        int i, cur;
        queue  que;
        que.push(s);
        memset(dist, -1, sizeof(dist));
        dist[s] = 0;
        while(!que.empty()){
            cur = que.front();
            que.pop();
            for(i = head[cur]; i != -1; i = edges[i].next)
                if(-1 == dist[edges[i].v] && edges[i].w){
                    dist[edges[i].v] = dist[cur] + 1;
                    que.push(edges[i].v);
                }
        }

        return dist[t] != -1;
    }

    int DFS(int start, int curFlow)
    {
        if(start == t)
            return curFlow;
        int i, minFlow = 0, v, temp;
        for(i = head[start]; i != -1; i = edges[i].next){
            v = edges[i].v;
            if(dist[start] == dist[v] - 1 && edges[i].w > 0){
                temp = DFS(v, min(edges[i].w, curFlow));
                edges[i].w -= temp;
                edges[i^1].w += temp;
                curFlow -= temp;
                minFlow += temp;
                if(0 == curFlow)
                    break;
            }
        }
        if(0 == minFlow)
            dist[start] = -2;
        return minFlow;
    }

    int maxFlow()
    {
        int res = 0;
        while(BFS()){
            res += DFS(s, INF);
        }
        return res;
    }
}G;

bool edges[MAX_N][MAX_N];
int edgeNum, nodeNum;

int netFlow(int s, int t)
{
    G.init(s + nodeNum, t);
    int i, j;
    for(i = 0; i < nodeNum; i++){
        G.addEdge(i, i + nodeNum, 1);
        for(j = 0; j < nodeNum; j++)
            if(edges[i][j])
                G.addEdge(i + nodeNum, j, INF);
    }


    return G.maxFlow();
}

int main()
{
    //freopen("in.txt", "r", stdin);

    int i, j, u, v, res;

    while(~scanf("%d%d", &nodeNum, &edgeNum)){
        memset(edges, 0, sizeof(edges));
        for(i = 0; i < edgeNum; i++){
            scanf(" (%d,%d)", &u, &v);
            edges[u][v] = edges[v][u] = true;
        }

        res = INF;
        for(i = 0; i < nodeNum; i++)
            for(j = 0; j < nodeNum; j++)
                if(!edges[i][j] && j != i)
                    res = min(res, netFlow(i, j));

        if(res == INF){
            if(!nodeNum || !edgeNum && nodeNum != 1)
                printf("0\n");
            else
                printf("%d\n", nodeNum);
        }
        else
            printf("%d\n", res);
    }
    return 0;
}