【Java】用动态规划的方法查找最长公共子序列

最长公共子序列的概念

LCS是（Longest Common Subsequence）的缩写，即最长公共子序列。一个序列，如果是两个或多个已知序列的子序列，且是所有子序列中最长的，则为最长公共子序列。

比如，对于char x[]="aabcd";有顺序且相互相邻的aabc是其子序列，有顺序但是不相邻的abc也是其公共子序列。即，只要得出序列中各个元素属于所给出的数列，就是子序列。

再加上char y[]="12abcabcd";对比出才可以得出最长公共子序列abcd。

区别于最长公共子串

最长公共子串是寻找两个或多个已知字符串最长的子串。与最长公共子序列的区别在于子序列不必是连续的，而子串却必须是。

现有问题如下：

从键盘中输入两个字符串数组序列，求出它们的最长公共子序列的个数。

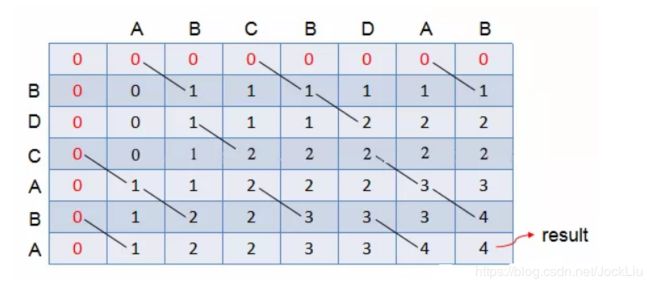
比如：X：A B C B D A B

           Y：B D C A B A

算法分析：

1.穷举法：根据题目的部分条件确定答案的大致范围，并在此范围内对所有可能的情况逐一验证，直到全部情况验证完毕。若某个情况验证符合题目的全部条件，则为本问题的一个解；若全部情况验证后都不符合题目的全部条件，则本题无解。这一算法不是不行，而是它有缺陷，那就是复杂度高，为O(n*2^m)，所以建议不用。

2.动态规划备忘录法：

计算采用递归方式，值计算出来之后将其保存起来以备它用。

比如 LCS问题：

首先将C[i,0](0≤i≤m)与C[0,j](1≤j≤n)初始化为0。

其余m×n个C[i,j]全部初始化为-1。

计算C[i,j]的递归算法LCS_L2(X,Y, i,j,C)（备忘录方法）：

若x[i]=y[j]，则去检查C[i-1,j-1]，若C[i-1,j-1]> -1（已经计算出来），就直接把C[i-1,j-1]+1赋给C[i,j]，返回。

若C[i-1,j-1]=-1（尚未计算出来），

就递归调用LCS_L2(X,Y, i-1,j-1,C) 计算出C[i-1,j-1]，

然后再把C[i-1,j-1]+1赋给C[i,j] ，返回。

若x[i] ¹ y[j]，则要检查C[i-1,j]和C[i,j-1]。

用图解释：

 

 

这种方法相对穷举法来说更简练，所以实用性很强

3.动态规划—自底向上法：

实现自底向上分析最常用的技术就是移进-规约分析，边移入边分析，一旦栈顶符号串形成某个句型的句柄或其他可归约串的时候就进行归约，归约的结果就是将句柄或其他可归约串从栈顶部分给弹出，然后将相应的非终结符压入栈中，重复这一个过程直到归约到栈中只剩文法的开始符号时则为分析成功，也就确定了输入串是文法的句子

实现代码如下：

备忘录法：

import java.util.Scanner;

public class 备忘录法查找最长公共子序列 {
	public static int lcs(char[] x, char[] y, int i, int j,int[][] bak) {
		//定义x，y字符串，i，j为他们的索引，从0开始 ，bak为他们的最长公共子序列统计值
		if (i == 0 || j == 0)//00位置的没有字符，所以返回0值。
			bak[i][j] = 0;
		else if (x[i] == y[j])
			bak[i][j] = lcs(x, y, i - 1, j - 1, bak) + 1;//搜索他们的相同字符值
		else
			bak[i][j] = max(lcs(x, y, i - 1, j, bak), lcs(x, y, i, j - 1, bak));
		//取他们之间最大的一个，
		return bak[i][j];
	}
	private static int max(int a, int b) {
		if (a > b)
			return a;
		return b;
	}
	public static void main(String[] args) {
		System.out.println("请输入X序列");//从键盘输入X序列
		Scanner s = new Scanner(System.in);
		String s1 = s.nextLine();
		char[] c1 = new char[s1.length() + 1];
		char[] t1 = s1.toCharArray();
		c1[0] = (char) 0;
		for (int i = 0; i < t1.length; i++) {
			c1[i + 1] = t1[i];
		}
		System.out.println("请输入Y序列");
		String s2 = s.nextLine();//从键盘输入Y序列
		char[] c2 = new char[s2.length() + 1];
		char[] t2 = s2.toCharArray();
		c2[0] = (char) 0;
		for (int i = 0; i < t2.length; i++) {
			c2[i + 1] = t2[i];
		}
		int[][] bak = new int[c1.length][c2.length];
		for (int i = 0; i < c1.length; i++) {
			for (int j = 0; j < c2.length; j++) {
				bak[i][j] = -1;
			}
		}
		System.out.println(lcs(c1, c2, c1.length - 1, c2.length - 1, bak));
	}
}

自底向上法：

public class 自底向上法 {
	
	public static int lcs(char[] x , char[] y,int i ,int j,int[][] bak) {
		for(int ii = 0 ; ii <= i ; ii++) {
			for(int jj = 0 ; jj <= j; jj++) {
				if(ii == 0 || jj == 0) bak[ii][jj] = 0;
				else if(x[ii] == y[jj]) bak[ii][jj] = bak[ii - 1][jj - 1] + 1;
				else bak[ii][jj] = max(bak[ii - 1][jj],bak[ii][jj - 1]);
			}
		}
		
		return bak[i][j];
	}
	
	private static int max(int a, int b) {
		if(a > b) return a;
		return b;
	}

	public static void main(String[] args) {
		System.out.println("请输入X序列");//从键盘输入X序列
		Scanner s = new Scanner(System.in);
		char[] c1 = new char[s1.length() + 1];//带0号字符的字符数组
		char[] t1 = s1.toCharArray();
		c1[0] = (char)0;
		for(int i = 0 ; i < t1.length ; i++) {
			c1[i + 1] = t1[i];
		}
		System.out.println("请输入Y序列");
		String s2 = s.nextLine();//从键盘输入Y序列
		char[] c2 = new char[s2.length() + 1];//带0号字符的字符数组
		char[] t2 = s2.toCharArray();
		c2[0] = (char)0;
		for(int i = 0 ; i < t2.length ; i++) {
			c2[i + 1] = t2[i];
		}
		
		int[][] bak = new int[c1.length][c2.length];
		
		
		System.out.println(lcs(c1,c2,c1.length - 1,c2.length - 1,bak));
	}
}

输出结果如图：