二维线段树
一维线段树用来维护一维的空间,即一个线段。
二维线段树用来维护二维的空间,即一个矩形。
二维线段树的每个结点都是一棵一维线段树,所以结构体数组要开二维,再加上线段树本身的性质,会占用很大内存,要尽量减少结构体内存储的值的个数和长度,考虑到每个节点表示的线段的左右端点可以作为函数参数,所以不再储存在结构体内部,若题目只需保存一个值,完全可以只开一个数组而不使用结构体。
第一维树维护的相当于矩形宽的一部分,每个节点对应的二维的线段树表示在当前宽的这部分里,长对应的数值。
比如说有一个2*3的矩阵:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
我们要保存这个矩阵,需要开二维数组:
int tree[2*4][3*4];一维的2表示矩阵的宽,二维的3表示矩阵的长。
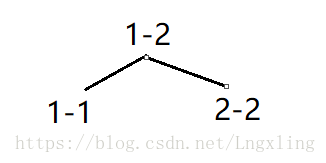
一维的线段树:
其中每个节点都表示一个二维的线段树,
tree[1]里的线段树表示对于1-2的宽,每个长度区间的对应值
tree[2]里的线段树表示对于1-1的宽,每个长度区间的对应值
二维的线段树:
tree[1][1]表示宽为1-2,长为1-3的矩形,即整个矩形
tree[2][3]表示宽为1-1,长为3-3的矩形
因此,矩阵里的每个值都存在一维线段树的叶节点对应的二维线段树的叶子节点上
即tree[2][4]=1 tree[2][5]=2 tree[3][3]=6
二维线段树可以用来进行矩形上的点更新,点查询,区间更新,区间查询。
点更新点查询:
每个点由一维的“坐标“和二维的”坐标“共同构成,查找时,先在第一维的线段树上找到对应的叶子节点,再进入叶子节点对应的二维的线段树中查找二维坐标。
void upda(int i,int x,int nl,int nr,int id)
{
if(nl==nr)
{
tree[id][i]=1;
return;
}
int mid=(nl+nr)>>1;
if(x<=mid)
upda(i<<1,x,nl,mid,id);
else
upda(i<<1|1,x,mid+1,nr,id);
tree[id][i]=tree[id][i<<1]+tree[id][i<<1|1];
}
void updata(int i,int x,int y,int nl,int nr)
{
if(nl==nr)
{
upda(1,y,1,m,i);
return;
}
int mid=(nl+nr)>>1;
if(x<=mid)
updata(i<<1,x,y,nl,mid);
else
updata(i<<1|1,x,y,mid+1,nr);
}
int que(int i,int x,int nl,int nr,int id)
{
if(nl==nr)
{
return tree[id][i].w;
}
int mid=(nl+nr)>>1;
if(x<=mid)
return tree[id][i].w%2+que(i<<1,x,nl,mid,id);
else
return tree[id][i].w%2+que(i<<1|1,x,mid+1,nr,id);
}
int query(int i,int x,int y,int nl,int nr)
{
if(nl==nr)
return que(1,y,1,n,i);
int mid=(nl+nr)>>1;
if(x<=mid)
return que(1,y,1,n,i)+query(i<<1,x,y,nl,mid);
else
return que(1,y,1,n,i)+query(i<<1|1,x,y,mid+1,nr);
}区间更新区间查询:
查找矩阵x1,y1,x2,y2,先在第一维线段树中查找x1-x2区间,再更新相应的线段树中的y1-y2。
void upda(int i,int l,int r,int nl,int nr,int id)
{
if(l==nl&&r==nr)
{
tree[id][i].w++;
tree[id][i].w%=2;
return;
}
int mid=(nl+nr)>>1;
if(r<=mid)
upda(i<<1,l,r,nl,mid,id);
else if(l>mid)
upda(i<<1|1,l,r,mid+1,nr,id);
else
{
upda(i<<1,l,mid,nl,mid,id);
upda(i<<1|1,mid+1,r,mid+1,nr,id);
}
}
void updata(int i,int l,int r,int nl,int nr,int dl,int dr)
{
if(l==nl&&r==nr)
{
upda(1,dl,dr,1,n,i);
return;
}
int mid=(nl+nr)>>1;
if(r<=mid)
updata(i<<1,l,r,nl,mid,dl,dr);
else if(l>mid)
updata(i<<1|1,l,r,mid+1,nr,dl,dr);
else
{
updata(i<<1,l,mid,nl,mid,dl,dr);
updata(i<<1|1,mid+1,r,mid+1,nr,dl,dr);
}
}
int que(int i,int l,int r,int nl,int nr,int id)
{
if(l==nl&&r==nr)
{
return tree[id][i];
}
int mid=(nl+nr)>>1;
if(r<=mid)
return que(i<<1,l,r,nl,mid,id);
else if(l>mid)
return que(i<<1|1,l,r,mid+1,nr,id);
else
return que(i<<1,l,mid,nl,mid,id)+que(i<<1|1,mid+1,r,mid+1,nr,id);
}
int query(int i,int l,int r,int nl,int nr,int dl,int dr)
{
if(l==nl&&r==nr)
{
return que(1,dl,dr,1,m,i);
}
int mid=(nl+nr)>>1;
if(r<=mid)
return query(i<<1,l,r,nl,mid,dl,dr);
else if(l>mid)
return query(i<<1|1,l,r,mid+1,nr,dl,dr);
else
return query(i<<1,l,mid,nl,mid,dl,dr)+query(i<<1|1,mid+1,r,mid+1,nr,dl,dr);
}区间更新点查询时可以不断累加路径上的价值
要特别注意的是,区间更新时要把子节点对应的树上的价值更新到父节点对应的树上,这样在区间查询时才能保证较小的复杂度
void up(int i,int x,int nl,int nr,int id)
{
tree[id][i]=tree[id<<1][i]+tree[id<<1|1][i];
if(nl==nr)
return;
int mid=(nl+nr)>>1;
if(x<=mid)
up(i<<1,x,nl,mid,id);
else
up(i<<1|1,x,mid+1,nr,id);
}
void updata(int i,int x,int y,int nl,int nr)
{
if(nl==nr)
{
upda(1,y,1,m,i);
return;
}
int mid=(nl+nr)>>1;
if(x<=mid)
updata(i<<1,x,y,nl,mid);
else
updata(i<<1|1,x,y,mid+1,nr);
up(1,y,1,m,i);
}