本周AI热点回顾:何恺明RegNet超越EfficientNet、数学难题“abc猜想”封印终被开启、微软麻将 AI 论文发布...
![]()
01
何恺明团队最新力作RegNet:
超越EfficientNet,GPU上提速5倍
还是熟悉的团队,还是熟悉的署名,Facebook AI实验室,推陈出新挑战新的网络设计范式。熟悉的Ross,熟悉的何恺明,他们带来全新的——RegNet。
不仅网络设计范式与当前主流“背道而驰”:简单、易理解的模型,也可以hold住高计算量。而且在类似的条件下,性能还要优于EfficientNet,在GPU上的速度还提高了5倍!
新的网络设计范式,结合了手动设计网络和神经网络搜索 (NAS)的优点:和手动设计网络一样,其目标是可解释性,可以描述一些简单网络的一般设计原则,并在各种设置中泛化。又和NAS一样,能利用半自动过程,来找到易于理解、构建和泛化的简单模型。
论文毫无疑问也中了CVPR 2020。
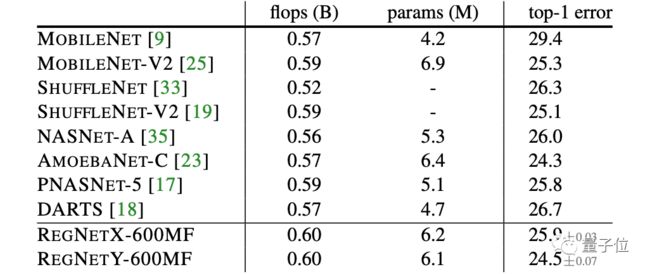
三组实验对比,近乎“大满贯”,实验在ImageNet数据集上进行,目标非常清晰:挑战各种环境下的神经网络。
与一众流行移动端神经网络的比较结果如下所示。
上表就是600MF的RegNet,与这些网络比较的结果。可以看出,无论是基于手动设计还是NAS的网络,RegNe的表现都很出色。
何恺明团队强调,RegNet模型使用基本的100 epoch调度(schedule),除了权重衰减外,没有使用任何正则化。
而大多数移动网络使用更长的调度,并进行了各种增强,例如深度监督、Cutout、DropPath等等。
论文地址:
https://arxiv.org/pdf/2003.13678.pdf
信息来源:量子位
02
十行代码让你的单机“影分身”,分布式训练速度快到飞起
参数服务器是分布式训练领域普遍采用的编程架构,主要包含Server和Worker两个部分,其中Server负责参数的存储和更新,而Worker负责训练。
飞桨的参数服务器功能也是基于这种经典的架构进行设计和开发的,同时在这基础上进行了SGD(Stochastic Gradient Descent)算法的创新(Geometric Stochastic Gradient Descent)。当前经过大量的实验验证,最佳的方案是每台机器上启动Server和Worker两个进程,而一个Worker进程中可以包含多个用于训练的线程。
飞桨参数服务器功能支持三种模式,分别是同步训练模式、异步训练模式和GEO异步训练模式。
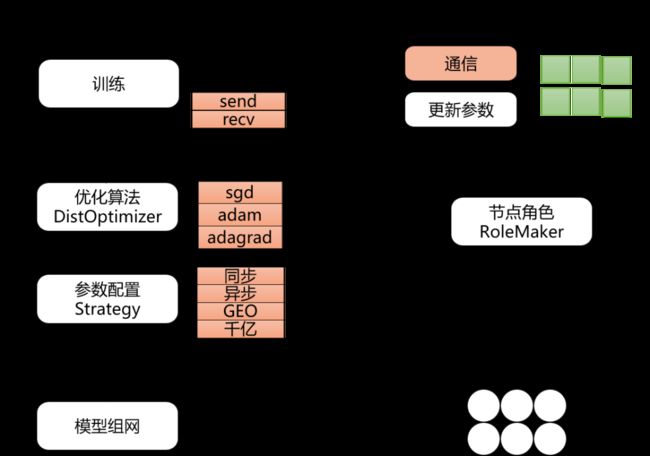
飞桨的分布式训练功能不仅包含参数服务器(同步、异步、GEO)模式,还包含collective、hybrid等其它模式。为了能让开发者们方便得使用这些功能,飞桨的工程师们非常贴心的专门为分布式训练设计了一套FleetAPI接口。如下图所示,使用FleetAPI可以轻松的将原先的单机训练转换为分布式参数服务器模式:
使用RoleMaker为参与训练的机器创建Worker和Server进程。RoleMaker有多种实现可适配用户的Kubernetes、MPI等环境。
使用Strategy和distributed_optimizer配置训练模式、优化函数以及计算图的拆分方案。在拆分计算图的过程中,Server和Worker中会被添加用于相互通信的算子。
初始化Worker和Server进程。
FleetAPI功能示意图
具体操作方法请参见下面的代码示例。
如下为模型单机训练的代码,为了简化说明,这里省略了模型网络定义和数据读取等部分的代码。
exe = Executor(place)
optimizer = optimizer.Adam(learning_rate=0.001)optimizer.minimize(avg_cost)exe.run(default_startup_program())
for batch_id, data in enumerate(train_reader()):avg_loss_value, auc_value = exe.run(main_program(), feed=feeder.feed(data))
用户只需要加入十行代码即可将上面的单机训练过程转换为分布式训练:
exe = Executor(place)#设置节点角色role = role_maker.PaddleCloudRoleMaker()fleet.init(role)optimizer = optimizer.Adam(learning_rate=0.001)#配置策略strategy = StrategyFactory.create_sync_strategy()optimizer = fleet.distributed_optimizer(optimizer, strategy)optimizer.minimize(avg_cost)# 初始化并运行Server进程if fleet.is_server(): fleet.init_server() fleet.run_server()# 初始化并运行Worker进程if fleet.is_worker(): fleet.init_worker()exe.run(fleet.startup_program)for batch_id, data in enumerate(train_reader()): avg_loss_value, auc_value = exe.run(fleet.main_program, feed=feeder.feed(data))# 通知Server停止监听Worker请求fleet.stop_worker()
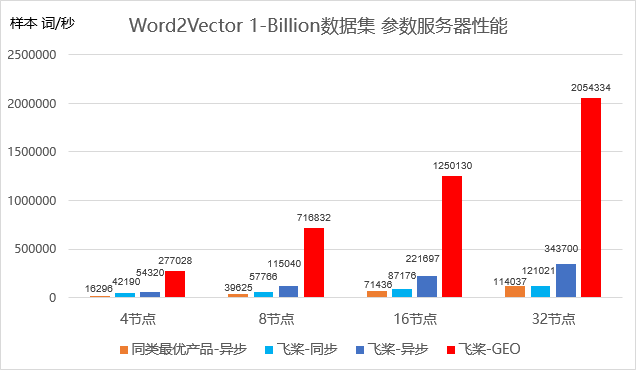
如下所示,在词向量Word2Vector模型上,采用GEO训练模式的飞桨分布式训练的训练速度能够超越同类最优产品 18倍。
Word2Vector模型性能示意图
信息来源:飞桨PaddlePaddle
03
数学难题“abc猜想”封印终被开启,望月新一论文终获发表
京都大学4月3日宣佈,该校数理解析研究所的教授望月新一(51岁)成功证明了30多年未被解决的数学难题“ABC猜想”。望月的论文通过了该研究所编撰的国际专业期刊《PRIMS》的审查并被採用。
该研究所评价称“解决了重要且困难的问题”。
刊登在期刊上的是望月新构筑的4篇关于“宇宙际Teichmüller理论”的论文,长达600页,从中得出的结论之一是能证明ABC猜想。据称还有助于证明关于整数的其他未解问题。
事实上,早在2012年,日本数学家望月新一(Shinichi Mochizuki)就在京都大学的数学系主页上上传了4篇论文,开放公众下载。
总长达500多页的论文(当代数学论文多为10~20页),里面充满了各种奇形怪状的符号,以及各种奇葩的定义名称,这是望月十几年前从数学界销声匿迹之后的首次露面。
望月论文一角
这次的“露面”,望月也带来了个“重磅炸弹”,他宣称自己已经解决了数学史上最富传奇色彩的未解猜想:ABC猜想。一时间,所有人都疯了般,纷纷去下载望月的论文来一探究竟,然而,却没有一个人能看得懂,就连华裔天才数学家陶哲轩也表示没看懂。
在论文中,望月自己构造了一个新的庞大的理论体系,并且命名为“宇宙际Teichmüller理论”(简称IUT理论),定义了各种前所未有的神秘术语,比如“宇宙暗边际之极”、“霍奇影院”(Hodge Theater)、“外星算数全纯结构”(alien arithmetic holomorphic structures)等。
其中,诺丁汉大学教授Ivan Fesenko在2014年就说他已经确认了证明的正确性,并对望月的工作给予了高度的评价,Fesenko认为,望月完全可以与代数几何的上帝格罗滕迪克相提并论,他说:“望月新一出现后,世界上就只有两种数学,望月之前的数学和望月之后的数学。”
abc猜想,也称Oesterlé–Masser猜想,最先由乔瑟夫·奥斯达利(Joseph Oesterlé)和大卫·马瑟(David Masser)在1985年提出。用三个相关的正整数a,b和c(满足a + b = c)声明此猜想(因此得名abc猜想)。
对于一个正整数n,找到它的所有质因数,把它们乘起来,得到的数叫做n的根基rad(n)。比如,60的质因数是2、3、5,所以rad(60) = 30.
假如有三个互质的正整数abc,c=a+b,那么c 通常小于rad(abc)。比如,a=2,b=7,c=a+b=9,这三个数互质;那么,abc=126,rad(126) = 42, 42>9.
有关望月新一所有的论文列表pdf:
http://www.kurims.kyoto-u.ac.jp/~motizuki/ronbun-list.pdf
信息来源:超级数学建模
04
微软麻将 AI 论文发布,首次公开技术细节
还记得去年 8 月微软发布的「雀神AI」Suphx 吗?今天,该研究团队在 arXiv 上发布了更新版的论文,进一步介绍了 Suphx 背后的技术。2019 年 8 月 29 日,微软发布了一个名为 Suphx(超级凤凰)的「麻将 AI」,在专业的麻将竞技平台上,Suphx 的实力胜过了顶级人类选手的平均水平。
当时一经发布,Suphx 便引起了广泛的关注,不仅是人工智能领域,不少麻将爱好者也都赶来围观讨论。人们评价该系统比战胜了职业围棋手的 AlphaGo 更复杂,被誉为「最强日麻人工智能」。
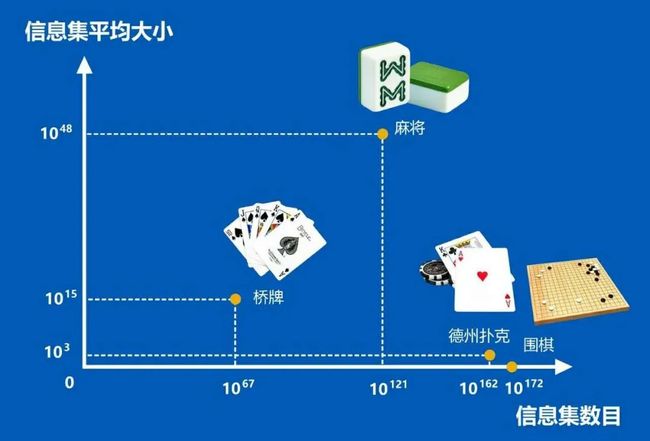
麻将的信息集数目和信息集平均大小
超过了桥牌、德扑和围棋
近日,该系统的研发团队在 arXiv 上发表了论文《Suphx: Mastering Mahjong with Deep Reinforcement Learning》(《Suphx:掌握麻将与深度强化学习》),更深一步地讲解了 Suphx 背后的技术。
Suphx 系统利用深度强化学习,从 5000 场比赛中学习、吸取经验之后,在日本专业的麻将竞技平台「天凤」上击败了众多麻将玩家,取得平台「特上房」的最高段位十段。
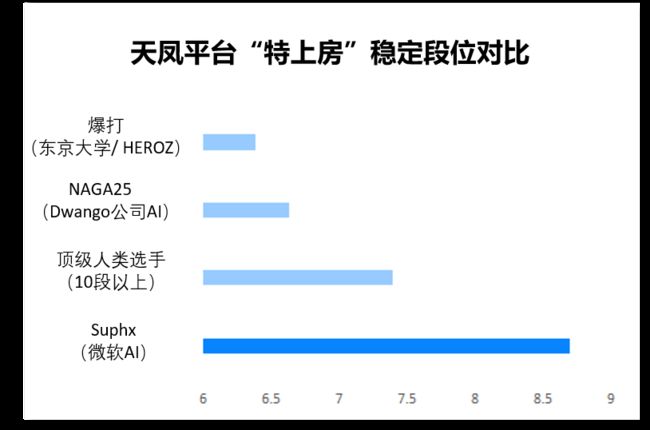
Suphx 在天凤平台的段位,远高于其它麻将 AI
从论文中得知,Suphx 在进一步的学习下,水平也更进一步。在拥有超过 35 万位玩家的「天凤」平台上,被官方评为水平超越 99.99% 以上玩家,这是计算机程序首次超过麻将中大多数顶级人类玩家。
Suphx 包含一系列卷积神经网络,它学习了五种模型来处理不同的场景,包括 discard(丢弃模型)、Riichi 模型、chow 模型、Pong 模型和 Kong 模型。在此基础上,Suphx 采用另一种基于规则的模型,来决定是否宣布赢家并进行下一轮,检查是否赢牌可以从其他玩家丢弃的牌中来判断,或者从排墙上抽出来的牌来判断。
在「天凤」平台与人类玩家进行了超过 5760 场比赛后,Suphx 创造了十段的纪录——大约只有 180 个玩家曾经达到过这个水平。而 Suphx 稳定的排名是 8.74 段(人类玩家最高水平是 7.4 段)。
《Suphx:掌握麻将与深度强化学习》论文地址:
https://arxiv.org/pdf/2003.13590.pdf
信息来源:HyperAI超神经
05
本周论文推荐
【CVPR2020|百度】ActBERT: Learning Global-Local Video-Text Representations
作者:Linchao Zhu, Yi Yang
论文介绍:
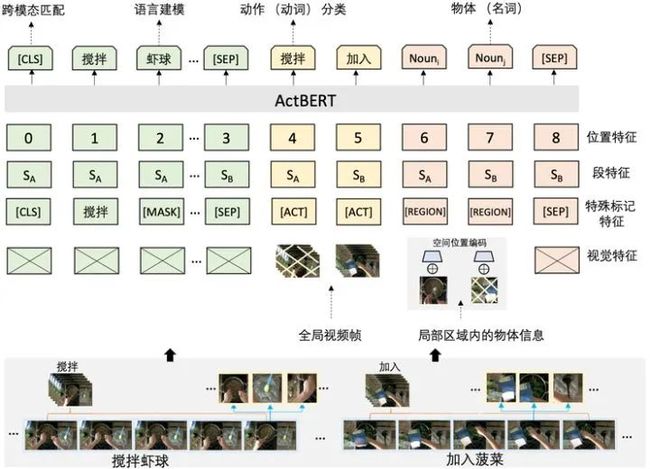
受到BERT在自我监督训练中的启发,百度团队对视频和文字进行类似的联合建模, 并基于叙述性视频进行视频和文本对应关系进行研究。其中对齐的文本是通过现成的自动语音识别功能提供的,这些叙述性视频是进行视频文本关系研究的丰富数据来源。ActBERT加强了视频文字特征,可以发掘到细粒度的物体以及全局动作意图。百度团队在许多视频和语言任务上验证了ActBERT的泛化能力,比如文本视频片段检索、视频字幕生成、视频问题解答、动作分段和动作片段定位等,ActBERT明显优于最新的一些视频文字处理算法,进一步证明了它在视频文本特征学习中的优越性。
END
![]()