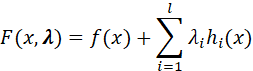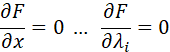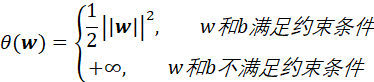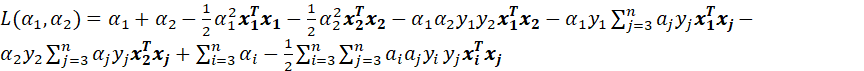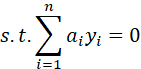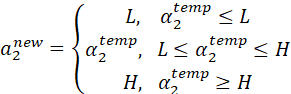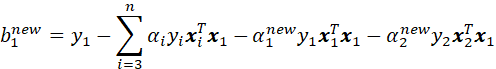SVM支持向量机 学习笔记

问题

训练样本集。分类学习的基本思想是在训练集D所在的样本空间找到一个划分超平面，将不同类别的样本划分开。在样本空间中，划分超平面可以通过如下线性方程来描述：

                                                          (1)

原因：

在划分超平面线性方程中，为法向量，决定了超平面的方向，b为位移项，决定了超平面与原点之间的距离。显然，一个划分超平面可以通过法向量w和位移项b确定，可以记作(w, b)。

 

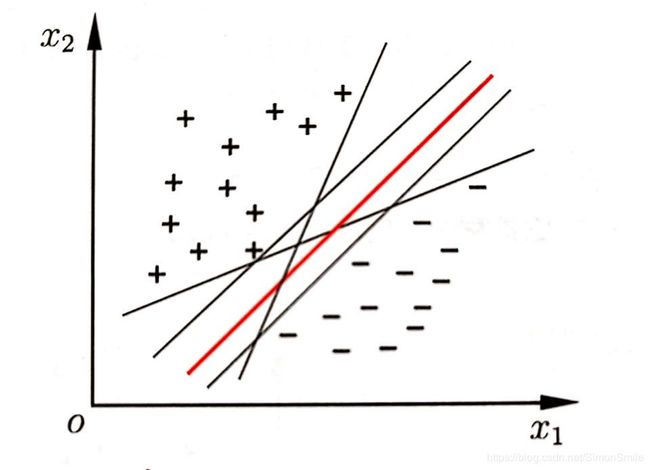
但是能将训练样本分开的超平面可能有很多，如下图所示，存在多个划分超平面可以将两类训练样本分开，应该找哪一个呢？

直观得看，应该去找位于两类训练样本“正中间”的划分超平面，即图中红色的那个，因为该划分超平面对训练样本可能存在的局部扰动的“容忍”性最好。例如，由于训练集的局限性或噪声的影响，训练集外的样本可能会比上图中的训练样本更接近分割界，这将使许多划分超平面出现错误，而红色的超平面受影响最小。换言之，这个划分超平面所产生的分类结果是最“鲁棒“的，对未见样本的泛化性最强。

接下来，我们将上述想要“找到泛化性最好的超平面“的思想用数学的形式表示出来。

对于划分超平面(w, b)和样本空间中的任意点x，样本空间中任意点x到划分超平面(w, b)的距离为

                                                      (2)

如果假设超平面(w, b)能将训练样本正确分类，那么对于，若，就有；若，则有。这两个不等式可以构成一个约束，但如果想要“找到泛化性最强”的超平面，这一约束是不够的，因为该约束只能保证找到正确划分的超平面，而无法表示出“所得超平面泛化性最强”的要求。

因此对这两个不等式做一些修改，令

                                     (3)

该不等式的推导稍后给出。我们先来看这个约束，如下图所示，

图中用圆圈圈起来的样本点是距离超平面最近的几个训练样本点，这些样本点使得（3）式的等号成立，它们被称为“支持向量”，两个异类支持向量到超平面的距离之和为，

                                                          (4)

称为“间隔”。接下来给出（3）式推导过程和间隔距离（4）的推导过程。

(3)式推导过程：

式（4）间隔距离推导过程：

我们希望能找到泛化性最强的划分超平面，就等价于希望能找到“间隔最大”的划分超平面，因为显然间隔越大，对误差样本的容错性就越大，泛化性就越强。也就是说，要找到能满足式（3）约束的参数w和b，使得γ最大，即：

                                                                (5)

将最大化中的分式倒转，转为最小化：     

                           （6）                                               

    

这就是支持向量机的基本型。

 

 

解决方法

我们希望求解式（6）得到大间隔划分超平面的模型参数w和b，就能得到划分超平面所对应的模型

观察目标函数式（6），这是一个在由不等式约束规定的可行区域内求最小值问题。一般来说，最优化问题有以下三种情况：

• 1 无约束条件

这是最简单的情况，解决方法通常是对函数变量求导，令求导函数为0的点可能是极值点。将结果带回原函数进行验证即可。

• 2 等式约束

设目标函数为，约束条件为，形如

“s.t.”表示subject to，为“受限于”的意思；l表示有l个约束条件。

解决方法是拉格朗日乘数法。定义拉格朗日函数：

其中为各约束条件的拉格朗日乘子。然后求解各变量的偏导方程：

求出方程组的解就是可能的最优值，将结果带回原函数进行验证即可。

• 3 不等式约束

设目标函数为，约束等式为，约束不等式为。此时优化问题描述如下

同样的，我们把所有的等式、不等式约束与f(x)写入一个式子，即拉格朗日函数：

和分别为约束等式和约束不等式对应的拉格朗日乘子。然后使用KKT条件，KKT条件是拉格朗日乘子法的一种泛化，是求解出最优值的必要条件。KKT条件是说最优值必须满足以下条件：

 

显然，我们的目标函数式（6）为第三种情况——不等式约束类型，那么我们首先对式（6）的每条约束添加拉格朗日乘子，则该问题的拉格朗日函数可写为

                                                                  (7)

其中，. 注意，因为要求，所以应将转化为，而不是.

 

现在令，那么有

• 如果w和b取值违反不等式约束条件，即，那么为正值，可令为正无穷，此时的最大值为正无穷，即为正无穷。
• 如果w和b取值满足不等式约束条件，即，那么为负值，此时的最大值为，即。

从以上两种情况分析可以得出：

那么在满足约束条件下有：，也就是说原始优化问题与新优化问题与等价，那么就可以将原始优化问题转化为新优化问题，新的优化问题为

                                                                 （8）

p*为优化问题的最优解。

 

接着观察这个优化式(8)，为先求最大值，再求最小值。但是观察内层的最大化，就要面对两个待求的参数w和b，且有不等式约束，求解比较困难。这时我们可以利用拉格朗日方程的对偶性，将最小和最大的位置调换一下，这样就变成了：

                                                                                           (9)

最小最大交换后的问题(9)是问题(8)的对偶问题，d*为这个对偶问题的最优解。

拉格朗日对偶具有一定的性质：原问题与对偶问题的最优解，在满足某些条件的情况下，两者相等。可以通过求解原问题的对偶问题，得到原问题的最优解。这样做的优点在于：（1）对偶问题往往更容易求解；（2）可以自然得引入核函数，进而推广到非线性分类问题。而使得p*=d*的“某些条件”就是KKT条件(这是不是很巧)，以及这个优化问题必须为凸优化问题。

那么将KKT条件应用到该问题中即要求，

于是，对于任意样本，总有或。若，则它不会对模型产生影响，若，那么必然，即，所对应样本必然位于最大间隔边界上，是一个支持向量。这个性质在后面会用到。 

 

接下来，就是正式开始求解式（9）。首先求解内部最小化，固定，要让L(w,b,α)关于w和b最小化，此时实际上就是上面说的三类优化问题的第一类。令对w和b的偏导为0可得：

                                                                                                     (10)

                                                                                                          (11)

将式（10）式（11）带入式（9），再考虑式（11）的约束，就能得到

                                                        (12)

推导过程：

至此，内侧最小化的步骤完成，得到式(12)。可以看出式(12)中只含有一个变量α。求解出α后，再求出w和b即可得到划分超平面模型。

 

那么，如何求解式(12)呢，可以采用高效的SMO（sequence minimal optimization）算法。

SMO算法将大优化问题分解为多个小优化问题来求解。这些小优化问题往往比较容易求解，并且对它们进行顺序求解的结果与整体求解的结果完全一致。具体来说，在中，SMO每次随机选择两个变量（当然可以是任意和，因为SMO是随机选择的，但为了书写方便，在这里我使用表示为两个随机变量），固定其他参数，然后求解式（12）以更新，直至收敛。

那么接下来我们固定两个变量，进行推导，目标函数就变成了

（13)

计算过程：

为了方便描述，定义如下符号：

最终目标函数变为

 (14)

需要时时牢记，此时我们假设，为变量，固定其他的参数均为常量。我们可以不用关心常量部分，因为常量在求导后均为0。现在目标函数中有两个变量，根据约束条件可以用表示，使得目标函数中只有一个变量。由约束条件可以得出

B为常量。

将上述等式两边同乘，得到

将的表达式代入得到

 (15)

这样目标函数中就只剩下了，令求导为0得到：

                                                                             (16)

计算过程：

令

为误差率，为学习率。再根据已知公式：

 可以将继续化简得：

                                                                           (17)

推导过程：

 至此，我们根据求解（12）式得到了的更新值。       

 

但是这样就行了吗？nonono，鲁迅（我）说，我们考虑问题一定要全面。并不是无拘无束的，它是受到一定限制的。

首先，对于任意，都有；其次，实际上我们上面所有的讨论都存在一个假设，即数据100%线性可分，但是事实上数据几乎都不会那么“完美”，因此需要引入一个“松弛变量”，使得允许有些数据点可以处于超平面错误的一侧，约束条件因此变为：

此外，观察（12）式，还有一个重要的约束为

因此有

假设取值的上下界为L和H，即

如果，有，所以有

如果\，有，那么有

以上就是的取值范围。

综上，得到：

 

 

已知，接下来我们根据和的关系求。再次根据式（12），且SMO每次只更新两个参数的原则，有

将上面两式相减，得到：

这样，我们就是知道了如何更新和。

此时——还有一个参数等待着更新，这个参数就是——参数b。很显然通过更新和，再通过式（10）可以实现参数w的更新，但是别忘了b也是参数之一，收敛过程中它也需要被更新。

这里我们考虑（或，两者其实是一样的），当在0和C之间时，根据KKT条件可知，

将等式两边同时乘，得到

将和单独提取出来，得到

 

等式右边前两项有

将带入上面等式得

同理得

综上有

 

至此，我们得到了、和b的更新方法。不断循环迭代这个过程直至收敛，就能得到开头，我们希望得到的划分超平面模型：

 

 

 

算法总结

综上所述，总结算法步骤：

• 1 使用启发式方法选取一对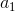和。

   1）扫描所有的乘子（），选取第一个违反KKT条件的乘子令其为

   2）在所有不违反KKT条件的乘子中，选取使最大的乘子令其为

• 2 固定其他参数，根据式（12）更新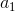和

   1）计算误差和。

   2）计算上下界

   3）计算学习率η

    4）更新

    5）更新

    6）更新b

 

 

 

 

参考资料

 

https://blog.csdn.net/c406495762/article/details/78072313#2-smo%E7%AE%97%E6%B3%95

https://blog.csdn.net/v_july_v/article/details/7624837

https://zhuanlan.zhihu.com/p/31886934

 

 

 

有问题的地方请指正~