【机器学习基础】Hessian矩阵

本系列为《模式识别与机器学习》的读书笔记。

一，Hessian 矩阵

反向传播也可以⽤来计算误差函数的⼆阶导数，形式为
$$\frac{{\partial }^{2}E}{\partial w_{ji}\partial w_{kl}}$$

注意，有时将所有的权值和偏置参数看成⼀个向量（记作 $\mathbf{w}$ ）的元素 $w_i$ 更⽅便，此时⼆阶导数组成了Hessian矩阵 $\mathbf{H}$ 的元素 $H_{ij}$ ，其中 $i,j\in \{1,\dots ,W\}$ ，且 $W$ 是权值和偏置的总数。Hessian矩阵在神经⽹络计算的重要的作⽤，包括：

1）⼀些⽤来训练神经⽹络的⾮线性最优化算法是基于误差曲⾯的⼆阶性质的， 这些性质由Hessian矩阵控制（Bishop and Nabney, 2008）；
2）对于训练数据的微⼩改变，Hessian矩阵构成了快速重新训练前馈⽹络的算法的基础 （Bishop, 1991）；
3）Hessian矩阵的逆矩阵⽤来鉴别神经⽹络中最不重要的权值，这是⽹络“剪枝”算法的⼀部分 （LeCun et al., 1990）；
4）Hessian矩阵是贝叶斯神经⽹络的拉普拉斯近似的核⼼。它的逆矩阵⽤来确定训练过的神经⽹络的预测分布，它的特征值确定了超参数的值，它的⾏列式⽤来计算模型证据。

二，对角近似

对于模式 $n$ ，Hessian矩阵的对角线元素可以写成

$$\frac{{\partial }^2{E}_n}{\partial w_{ji}^2}=\frac{{\partial }^2{E}_n}{\partial a_j^2}{z}_i^2\text{\hspace{1em}(5.56)}$$

从而，反向传播⽅程的形式为
$$\frac{{\partial }^2{E}_n}{\partial a_j^2}=h^{\prime }(a_j{)}^2\sum _k\sum _{k^{\prime }}{w}_{kj}{w}_{k^{\prime }j}\frac{{\partial }^2{E}_n}{\partial a_k\partial a_{k^{\prime }}}+h^{\prime \prime }(a_j)\sum _k{w}_{kj}\frac{\partial E_n}{\partial a_k}\text{\hspace{1em}(5.57)}$$
如果忽略⼆阶导数中⾮对角线元素， 那么有（Becker and LeCun, 1989; LeCun et al., 1990）
$$\frac{{\partial }^2{E}_n}{\partial a_j^2}=h^{\prime }(a_j{)}^2\sum _k{w}_{kj}^2\frac{{\partial }^2{E}_n}{\partial a_k^2}+h^{\prime \prime }(a_j)\sum _k{w}_{kj}\frac{\partial E_n}{\partial a_k}\text{\hspace{1em}(5.58)}$$

三，外积近似

当神经⽹络应⽤于回归问题时，通常使⽤下⾯形式的平⽅和误差函数
$$E=\frac{1}{2}\sum _{n=1}^N(y_n-t_n{)}^2\text{\hspace{1em}(5.59)}$$
考虑单⼀输出的情形（推⼴到多个输出是很直接的），可以把Hessian矩阵写成下⾯的形式
$$\mathbf{H}=\nabla \nabla E=\sum _{n=1}^N\nabla y_n(\nabla y_n{)}^T+\sum _{n=1}^N(y_n-t_n)\nabla \nabla y_n\text{\hspace{1em}(5.60)}$$
通过忽略公式(5.60)的第⼆项，我们就得到了 Levenberg-Marquardt近似，或者称为外积近似（outer product approximation）（因为此时Hessian矩阵由向量外积的求和构造出来），形式为
$$\mathbf{H}\simeq \sum _{n=1}^N{\mathbf{b}}_n{\mathbf{b}}_n^T\text{\hspace{1em}(5.61)}$$
其中 ${\mathbf{b}}_n\equiv \nabla a_n=\nabla y_n$ ， 因为输出单元的激活函数就是恒等函数。这种近似只在⽹络被恰当地训练时才成⽴， 对于⼀个⼀般的⽹络映 射，公式(5.60)的右侧的⼆阶导数项通常不能忽略。

在误差函数为交叉熵误差函数，输出单元激活函数为logistic sigmoid函数的神经⽹络中，对应的近似为
$$\mathbf{H}\simeq \sum _{n=1}^N{y}_n(1-y_n){\mathbf{b}}_n{\mathbf{b}}_n^T\text{\hspace{1em}(5.62)}$$
对于输出函数为softmax函数的多类神经⽹络，可以得到类似的结果。

四，Hessian 矩阵的逆矩阵

使⽤外积近似，可以提出⼀个计算Hessian矩阵的逆矩阵的⾼效⽅法（Hassibi and Stork, 1993）。⾸先，⽤矩阵的记号写出外积近似，即

$${\mathbf{H}}_N=\sum _{n=1}^N{\mathbf{b}}_n{\mathbf{b}}_n^T\text{\hspace{1em}(5.63)}$$
其中， ${\mathbf{b}}_n\equiv {\nabla }_{\mathbf{w}}{a}_n$ 是数据点 $n$ 产⽣的输出单元激活对梯度的贡献。

现在推导⼀个建⽴Hessian矩阵的顺序步骤，每次处理⼀个数据点。假设已经使⽤前 $L$ 个数据点得到了Hessian矩阵的逆矩阵。通过将第 $L+1$ 个数据点的贡献单独写出来，有
$${\mathbf{H}}_{L+1}={\mathbf{H}}_L+{\mathbf{b}}_{L+1}{\mathbf{b}}_{L+1}^T\text{\hspace{1em}(5.64)}$$
考虑下⾯的矩阵恒等式
$$(\mathbf{M}+\mathbf{v}{\mathbf{v}}^T{)}^{-1}={\mathbf{M}}^{-1}-\frac{({\mathbf{M}}^{-1}\mathbf{v})({\mathbf{v}}^{\mathbf{T}}{\mathbf{M}}^{-1})}{1+{\mathbf{v}}^T{\mathbf{M}}^{-1}\mathbf{v}}\text{\hspace{1em}(5.65)}$$
如果令 ${\mathbf{H}}_L=\mathbf{M}$ ，且 ${\mathbf{b}}_{L+1}=\mathbf{v}$ ，有
$${\mathbf{H}}_{L+1}^{-1}={\mathbf{H}}_L^{-1}-\frac{{\mathbf{H}}_L^{-1}{\mathbf{b}}_{L+1}{\mathbf{b}}_{L+1}^T{\mathbf{H}}_L^{-1}}{1+{\mathbf{b}}_{L+1}^T{\mathbf{H}}_L^{-1}{\mathbf{b}}_{L+1}}\text{\hspace{1em}(5.66)}$$
使⽤这种⽅式，数据点可以依次使⽤，直到 $L+1=N$ ，整个数据集被处理完毕。于是，这个结果表⽰⼀个计算Hessian矩阵的逆矩阵的算法， 这个算法只需对数据集扫描⼀次。最开始的矩阵 ${\mathbf{H}}_0$ 被选为 $\alpha \mathbf{I}$ ，其中 $\alpha$ 是⼀个较⼩的量，从⽽算法实际找的是 $\mathbf{H}+\alpha \mathbf{I}$ 的逆矩阵。

五，有限差

如果对每对可能的权值施加⼀个扰动，那么有
$$\begin{array}{rl}\frac{{\partial }^{2}E}{\partial w_{ji}{\partial }_{w_{lk}}}& =\frac{1}{4{ϵ}^2}\{E(w_{ji}+ϵ,w_{lk}+ϵ)-E(w_{ji}+ϵ,w_{lk}-ϵ)\\ & -E(w_{ji}-ϵ,w_{lk}+ϵ)+-E(w_{ji}-ϵ,w_{lk}-ϵ)+O({ϵ}^2)\}\end{array}\text{\hspace{1em}(5.67)}$$
通过使⽤对称的中⼼差，确保了残留的误差项是 $O({ϵ}^2)$ ⽽不是 $O(ϵ)$ 。 由于在Hessian矩阵中有 $W^2$ 个元素，且每个元素的计算需要四次正向传播过程，每个传播过程需要 $O(W)$ 次操作（每个模式），因此看到这种⽅法计算完整的Hessian矩阵需要 $O(W^3)$ 次操作。所以，这个⽅法的计算性质很差，虽然在实际应⽤中它对于检查反向传播算法的执⾏的正确性很有⽤。

⼀个更加⾼效的数值导数的⽅法是将中⼼差应⽤于⼀阶导数，⽽⼀阶导数可以通过反向传播⽅法计算。即
$$\frac{{\partial }^{2}E}{\partial w_{ji}{\partial }_{w_{lk}}}=\frac{1}{2ϵ}\left\{\frac{\partial E}{\partial w_{ji}}(w_{kl}+ϵ)-\frac{\partial E}{\partial w_{ji}}(w_{kl}-ϵ)\right\}+O({ϵ}^2)\text{\hspace{1em}(5.68)}$$
由于只需要对 $W$ 个权值施加扰动，且梯度可以通过 $O(W)$ 次计算得到，因此看到这种⽅法可以在 $O(W^2)$ 次操作内得到Hessian矩阵。

六，Hessian 矩阵的精确计算

考虑⼀个具有两层权值的⽹络，这种⽹络中待求的⽅程很容易推导，将使⽤下标 $i$ 和 $i^{\prime }$ 表⽰输⼊，⽤下标 $j$ 和 $j^{\prime }$ 表⽰隐含单元，⽤下标 $k$ 和 $k^{\prime }$ 表⽰输出。⾸先定义

$${\delta }_k=\frac{\partial E_n}{\partial a_k},M_{k{k}^{\prime }}=\frac{{\partial }^2{E}_n}{\partial a_k\partial a_{k^{\prime }}}$$

其中 $E_n$ 是数据点 $n$ 对误差函数的贡献。于是，这个⽹络的Hessian矩阵可以被看成三个独⽴的模块，即

1）两个权值都在第⼆层

$$\frac{{\partial }^2{E}_n}{\partial w_{kj}^{(2)}\partial w_{k^{\prime }{j}^{\prime }}^{(2)}}=z_j{z}_{j^{\prime }}{M}_{k{k}^{\prime }}\text{\hspace{1em}(5.69)}$$

2）两个权值都在第⼀层
$$\begin{array}{rl}\frac{{\partial }^2{E}_n}{\partial w_{ji}^{(1)}\partial w_{j^{\prime }{i}^{\prime }}^{(1)}}& =x_i{x}_{i^{\prime }}{h}^{\prime \prime }(a_{j^{\prime }})I_{j{j}^{\prime }}\sum _k{w}_{k{j}^{\prime }}^{(2)}{\delta }_k\\ & +x_i{x}_{i^{\prime }}{h}^{\prime }(a_{j^{\prime }})h^{\prime }(a_j)\sum _k\sum _{k^{\prime }}{w}_{k^{\prime }{j}^{\prime }}^{(2)}{w}_{kj}^{(2)}{M}_{k{k}^{\prime }}\end{array}\text{\hspace{1em}(5.70)}$$

3）每⼀层有⼀个权值
$$\frac{{\partial }^2{E}_n}{\partial w_{ji}^{(1)}\partial w_{k{j}^{\prime }}^{(2)}}=x_i{h}^{\prime }(a_j)\left\{{\delta }_k{I}_{j{j}^{\prime }}+z_{j^{\prime }}\sum _{k^{\prime }}{w}_{k^{\prime }j}^{(2)}{M}_{k{k}^{\prime }}\right\}\text{\hspace{1em}(5.71)}$$

其中，$I_{j{j}^{\prime }}$ 是单位矩阵的第 $j$, $j^{\prime }$ 个元素。

七，Hessian 矩阵的快速乘法

尝试寻找⼀种只需 $O(W)$ 次操作的直接计算 ${\mathbf{v}}^T\mathbf{H}$ 的⾼效⽅法。⾸先注意到
$${\mathbf{v}}^T\mathbf{H}={\mathbf{v}}^T\nabla (\nabla E)\text{\hspace{1em}(5.72)}$$

其中 $\nabla$ 表⽰权空间的梯度算符。然后，可以写下计算 $\nabla E$ 的标准正向传播和反向传播的⽅程， 继而得到⼀组计算 ${\mathbf{v}}^T\mathbf{H}$ 的正向传播和反向传播的⽅程（Møller, 1993; Pearlmutter, 1994）。这对应于将微分算符 ${\mathbf{v}}^T\nabla$ 作⽤于原始的正向传播和反向传播的⽅程。Pearlmutter（1994）使⽤记号 $\mathcal{R}\{\cdot \}$ 表⽰算符 ${\mathbf{v}}^T\nabla$ 。下⾯的分析过程很直接，会使⽤通常的微积分规则，以及下⾯的结果

$$\mathcal{R}\{\mathbf{w}\}=\mathbf{v}$$

使⽤⼀个简单的例⼦来说明这个⽅法，使⽤两层⽹络，以及线性的输出单元和平⽅和误差函数。考虑数据集⾥的⼀个模式对于误差函数的贡献。这样，所要求解的向量可以通过求出每个模式各⾃的贡献然后求和的⽅式得到。对于两层神经⽹络，正向传播⽅程为

$$\begin{gathered} a_j=\sum _i{w}_{ji}{x}_i \\ {z}_j=h(a_j) \\ {y}_k=\sum _j{w}_{kj}{z}_j \end{gathered}$$

现在使⽤ $\mathcal{R}\{\cdot \}$ 算符作⽤于这些⽅程上，得到⼀组正向传播⽅程，形式为

$$\begin{gathered} \mathcal{R}\{a_j\}=\sum _i{v}_{ji}{x}_i \\ \mathcal{R}\{z_j\}=h^{\prime }(a_j)\mathcal{R}\{a_j\} \\ \mathcal{R}\{y_k\}=\sum _j{w}_{kj}\mathcal{R}\{z_j\}+\sum _j{v}_{kj}{z}_j \end{gathered}$$

其中，$v_{ji}$ 是向量 $\mathbf{v}$ 中对应于权值 $w_{ji}$ 的元素。

由于考虑的是平⽅和误差函数，因此有下⾯的标准的反向传播表达式
$$\begin{gathered} {\delta }_k=y_k-t_k \\ {\delta }_j=h^{\prime }(a_j)\sum _k{w}_{kj}{\delta }_k \end{gathered}$$
将 $\mathcal{R}\{\cdot \}$ 算符作⽤于这些⽅程上，得到⼀组反向传播⽅程，形式为
$$\begin{gathered} \mathcal{R}\{{\delta }_k\}=\mathcal{R}\{y_k\} \\ \begin{array}{rl}\mathcal{R}\{{\delta }_j\}& =h^{\prime \prime }(a_j)\mathcal{R}\{a_j\}\sum _k{w}_{kj}{\delta }_k\\ & +h^{\prime }(a_j)\sum _k{v}_{kj}{\delta }_k+h^{\prime }(a_j)\sum _k{w}_{kj}\mathcal{R}\{{\delta }_k\}\end{array} \end{gathered}$$

最后，有误差函数的⼀阶导数的⽅程

$$\begin{gathered} \frac{\partial E}{\partial w_{kj}}={\delta }_k{z}_j \\ \frac{\partial E}{\partial w_{ji}}={\delta }_j{x}_i \end{gathered}$$

使⽤ $\mathcal{R}\{\cdot \}$ 算符作⽤在这些⽅程上，我们得到了下⾯的关于 ${\mathbf{v}}^T\mathbf{H}$ 的表达式

$$\begin{gathered} \mathcal{R}\left\{\frac{\partial E}{\partial w_{kj}}\right\}=\mathcal{R}\{{\delta }_k\}{z}_j+{\delta }_k\mathcal{R}\{z_j\} \\ \mathcal{R}\left\{\frac{\partial E}{\partial w_{ji}}\right\}=x_i\mathcal{R}\left\{{\delta }_j\right\} \end{gathered}$$

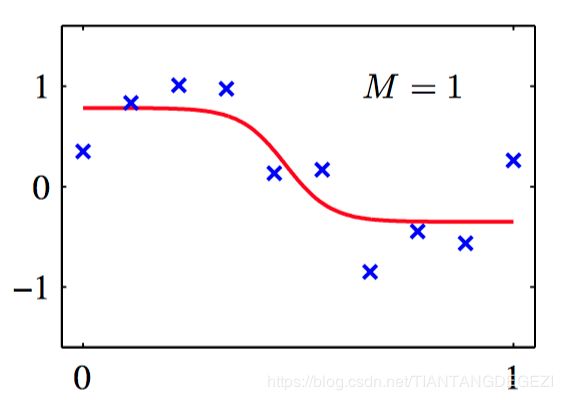
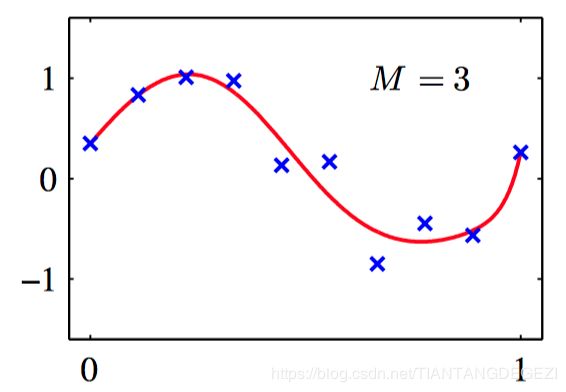
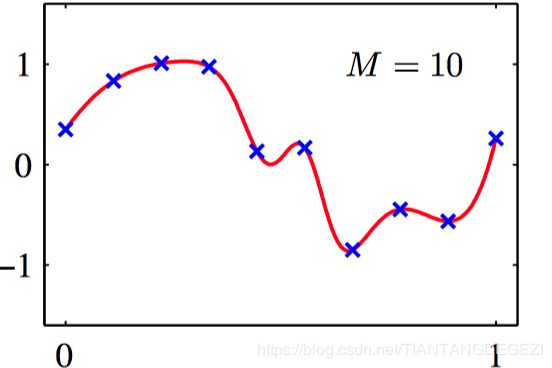
如图5.11～13，使⽤从正弦数据集中抽取的10个数据点训练的两层神经⽹络的例⼦。 各图分别给出了使⽤ $M=1,3,10$ 个隐含单元调节⽹络的结果，调节的⽅法是使⽤放缩的共轭梯度算法来最⼩化平⽅和误差函数。



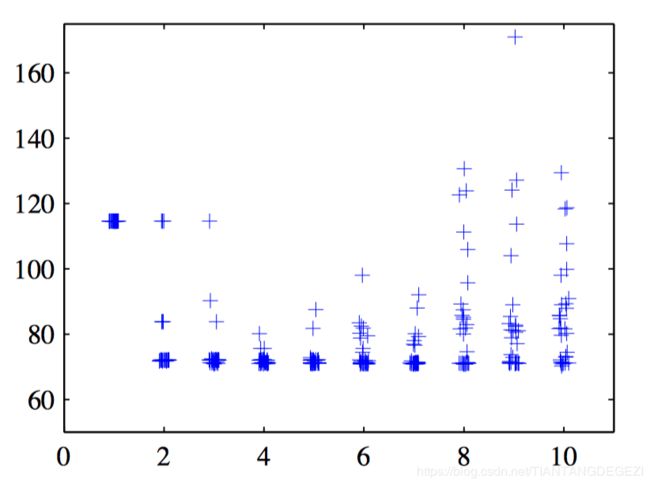
如图5.14，对于多项式数据集，测试集的平⽅和误差与⽹络的隐含单元的数量的图像。对于每个⽹络规模，都随机选择了30个初始点，这展⽰了局部最⼩值的效果。对于每个新的初始点，权向量通过从⼀个各向 同性的⾼斯分布中取样，这个⾼斯分布的均值为零，⽅差为10。