一维线段树详解
一、线段树的概念
线段树是用于区间处理的高效的数据结构,用二叉树来进行实现。
它主要分为两个步骤:修改和查询。
查询与修改的时间复杂度为O( l o g n logn logn)。
二、线段树的构造
我们利用递归来进行构造,从区间为( 1 1 1, n n n)的下标为 1 1 1的根开始递归。最终完成构造。
伪代码:
void push_up(int rt) //传递给父亲结点
{
tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];//左子节点,右子节点
}
void build_tree(int l, int r, int rt)//l和r代表区间,rt为根的点
{
lazy[rt] = 0;//lazy数组的初始化,后续我们会讲到,这里是个优化
if (l == r)//叶子节点
{
scanf("%d", &tree[rt]);
return;
}
int mid = (l + r) >> 1;
build_tree(l, mid, rt << 1);//左子树
build_tree(mid +1, r, rt << 1 | 1);//右子树
push_up(rt);//向上传递
}
build_tree(1, n, 1);
三、Lazy - tag 方法讲解(俗称懒标记)
主要用于区间修改问题上。
1、懒标记和未优化区间修改的对比
- 未优化的区间修改:我们如果一个数一个数的修改,我们单点修改的时间为O( l o g n logn logn),区间修改为O( n l o g n nlogn nlogn),但我们Q次操作的总复杂度为O( n 2 l o g n n^2logn n2logn)。
- 懒标记:如果[ L L L, R R R]在要修改的范围[ a a a, b b b]之间,则我们并不需要继续向下修改[ L L L, R R R],直接将lazy[rt]标记进行更新就可以,如果遇到下次将[ L L L, R R R]的区间进行破坏时([ a a a, b b b]不能完全覆盖[ L L L, R R R]),我们就需要将lazy[rt]数组下方,进行下面的修改,这样可以减小时间复杂度。总体时间复杂度为O( n l o g n nlogn nlogn)。
2、我们来用图示法进行一遍演示:
原来的线段树:
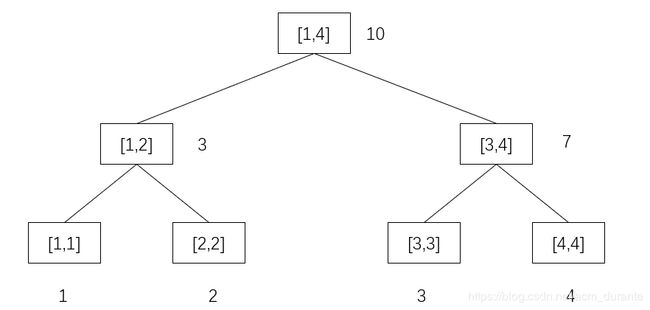
修改:将[ 1 1 1, 2 2 2]全部加上 5 5 5
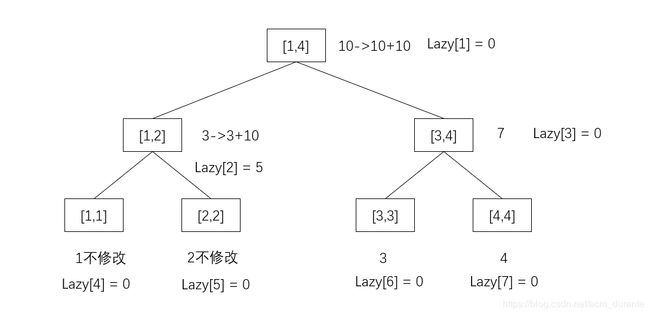
二次修改:破坏[ 1 1 1, 2 2 2]区间,将[ 1 1 1, 1 1 1]区间减去 1 1 1 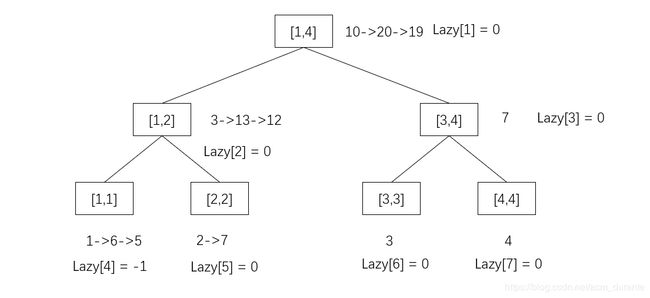
3、伪代码:
void push_down(int rt, int len) //lazy数组将子根进行修改
{
if (lazy[rt])
{
lazy[rt << 1] += lazy[rt];
lazy[(rt << 1) | 1] += lazy[rt];
tree[rt << 1] += (len - (len >> 1)) * lazy[rt];
tree[(rt << 1) | 1] += (len >> 1) * lazy[rt];
lazy[rt] = 0;
}
}
四、update函数(基于区间修改)
伪代码:
void update(int a, int b, ll c, int l, int r, int rt)
{
if (a <= l && b >= r)//区间【l,r】在【a,b】区间内,就可以调用lazy数组直接进行计算
{
tree[rt] += (r - l + 1) * c;
lazy[rt] += c;
return;
}
push_down(rt, r - l + 1);//查看是否需要lazy数组的下放
int mid = (l + r) >> 1;
if (a <= mid)//左区间
update(a, b, c, l, mid, rt << 1);
if (b > mid)//右区间
update(a, b, c, mid + 1, r, rt << 1 | 1);
push_up(rt);//将子根节点的计算值更新到父根
}
五、query函数
伪代码:
int query(int a, int b, int l, int r, int rt)
{
if (a <= l && b >= r)//区间【l,r】在【a,b】区间内
return tree[rt];
push_down(rt, r - l + 1);//查看是否需要lazy数组的下放
int mid = (l + r) >> 1;
int res = 0;
if (a <= mid)//左区间
res += query(a, b, l, mid, rt << 1);
if (b > mid)//右区间
res += query(a, b, mid + 1, r, rt << 1 | 1);
return res;
}
六、小结及题单及详解传送门
1、小结
线段树的情况复杂多样,可操作性十分强,要根据不同的题来进行修改,主要还是理解lazy数组及线段树如何使用,伪代码仅供参考,要灵活处理。
2、题单及详解传送门
未完待续…