最小生成树问题:算法分析 & Java 实现
一、简介
1. 什么是最小生成树
将一个有权图中的 所以顶点 都连接起来,并保证连接的边的 总权重最小,即最小生成树(mini spanning tree)问题。
例如,电子电路设计中,将所有组件的针脚连接在一起,且希望所使用的连线长度最短。
2. 图示
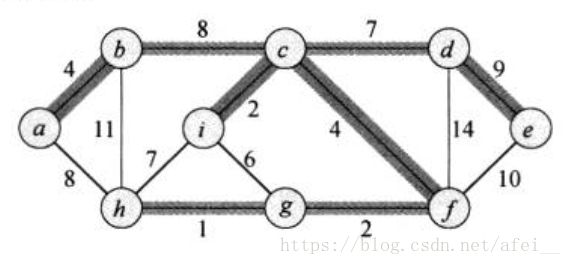
如上图(这里借用的是《算法导论》一书中的图)所示,每条边上的数字表示权重。我们使用阴影边连接了所有的顶点,并保证了其总权重是最小的。
注意最小生成树可能并不是唯一的,例如上图中我们就可以将 (b, c) 边换成 (a, h) 边。
二、算法分析
1. 怎么求解
解决最小生成树的问题通常有两种解法:Kruskal 算法和 Prim 算法。它们都属于 贪婪算法,即每次总是寻找局部最优解。下面我们以 Kruskal 算法为例分析和求解该问题。
2. Kruskal 算法
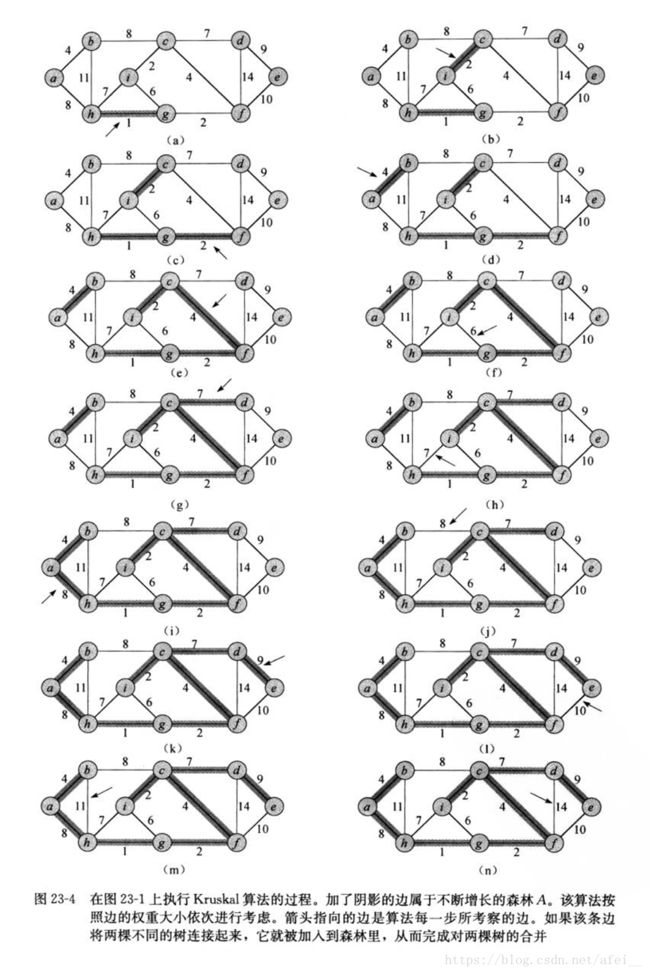
第一步,我们找出 权重最短 的边,并将边的顶点合并到一颗树中,例如 (g, h);
第二步,在剩余边中继续找出 权重最短 的边,并将边的顶点合并到一颗树中,例如 (c, i);
重复第二步,直到所有的顶点都合并到同一颗树中。
注意,如果某条边的两个顶点已经在同一颗树中了,则跳过该边,因为加入该边将导致闭环(它的两个顶点已经在同一颗树中连接了,没必要再加这条边了)。
3. 过程图解
三、代码实现
好了,理论说了这么多看着也乏味,关键是代码要怎么写呢?
1. Edge 类
我们算法最后返回的结果其实就是一个 “边” 的集合。我们很容易想到我们需要一个类来表示图的边,它应该包含两个顶点和权重这些信息,且之后我们需要根据边的权重从小到大排序,所以 Edge 类还应该实现 Comparable 接口。
public class Edge implements Comparable<Edge> {
private Vertex start;
private Vertex end;
private int weight; // 权重
public Edge(Vertex start, Vertex end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
public Vertex getStart() {
return start;
}
public Vertex getEnd() {
return end;
}
@Override
public int compareTo(Edge other) {
return this.weight - other.weight;
}
}
2. Vertex 类
上面 Edge 类里有两个顶点,这个顶点类当然也是需要的。由于算法之后需要判断两个顶点是否在同一个树中,那么最简单的方式就是判断顶点目前所在的树的根结点是否相同即可。
所以我们需要通过 Vertex 类找到树的根结点,可以创建一个 TreeNode 类表示树的结点,然后 Vertex 类继承 TreeNode 类,因为顶点可以看作就是树中的一个叶子结点。
public class Vertex extends TreeNode {
private char value; // 顶点的值
public Vertex(char value) {
this.value = value;
}
public char getValue() {
return value;
}
public TreeNode getRoot() {
TreeNode root = this;
while (root.getParent() != null) {
root = root.getParent();
}
return root;
}
public void setRoot(TreeNode treeNode) {
getRoot().setParent(treeNode);
}
}
其父类为:
public class TreeNode {
protected TreeNode parent;
public TreeNode getParent() {
return parent;
}
public void setParent(TreeNode parent) {
this.parent = parent;
}
}
3. 场景类
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Main {
public static void main(String[] args) {
List<Edge> edges = getTestData(); // 获取测试数据
List<Edge> result = miniSpanningTree(edges); // 得到最小生成树
printEdges(result); // 打印最小生成树的边
}
public static List<Edge> miniSpanningTree(List<Edge> edges) {
ArrayList<Edge> result = new ArrayList<>();
Collections.sort(edges); // 根据边权重从小到大排序
for (Edge edge : edges) {
Vertex u = edge.getStart();
Vertex v = edge.getEnd();
// 如果 u 和 v 已经在同一颗树里则跳过
if (u.getRoot() == v.getRoot()) {
continue;
}
result.add(edge);
// 将 u 和 v 放在同一颗树里
// 合并两个树最直接的办法就是使用一个新的根结点,然后连接两个子树
TreeNode newRoot = new TreeNode();
u.setRoot(newRoot);
v.setRoot(newRoot);
}
return result;
}
public static List<Edge> getTestData() {
ArrayList<Edge> list = new ArrayList<>();
Vertex[] vertexes = new Vertex[9];
for (int i = 0; i < vertexes.length; i++) {
// 'a' to 'i'
vertexes[i] = new Vertex((char) (i + 97));
}
list.add(new Edge(vertexes[0], vertexes[1], 4)); // a-b
list.add(new Edge(vertexes[0], vertexes[7], 8)); // a-h
list.add(new Edge(vertexes[1], vertexes[2], 8)); // b-c
list.add(new Edge(vertexes[1], vertexes[7], 11)); // b-h
list.add(new Edge(vertexes[2], vertexes[3], 7)); // c-d
list.add(new Edge(vertexes[2], vertexes[5], 4)); // c-f
list.add(new Edge(vertexes[2], vertexes[8], 2)); // c-i
list.add(new Edge(vertexes[3], vertexes[4], 9)); // d-e
list.add(new Edge(vertexes[3], vertexes[5], 14)); // d-f
list.add(new Edge(vertexes[4], vertexes[5], 10)); // e-f
list.add(new Edge(vertexes[5], vertexes[6], 2)); // f-g
list.add(new Edge(vertexes[6], vertexes[7], 1)); // g-h
list.add(new Edge(vertexes[6], vertexes[8], 6)); // g-i
list.add(new Edge(vertexes[7], vertexes[8], 7)); // h-i
return list;
}
public static void printEdges(List<Edge> edges) {
for (int i = 0; i < edges.size(); i++) {
Edge edge = edges.get(i);
System.out.println("(" + edge.getStart().getValue() + ", " + edge.getEnd().getValue() + ")");
}
}
}
4. 执行结果
(g, h)
(c, i)
(f, g)
(a, b)
(c, f)
(c, d)
(a, h)
(d, e)