白话空间统计三十:地统计学(2)前提假设
上文说到,地统计学有四个基础理论,分别是:
今天我们先来讲第一个基础原理:前提假设。
地统计学有的一共有三个前提假设,分别是:
随机过程——地统计学的主要研究对象
概率研究中,随机是一个非常重要的内容。通常说来在自然条件下,随机是最完美的结果,随机表示了机会均等,表示无规律,无法预测,表示一切都是平滑的。在没有外在影响力的情况下,理论上一切都应该是随机的。
随机过程是概率论里面的一个核心概念——同学们可能都不是学统计的(或者,大学概率论上课时候时候也和虾神一样,目瞪口呆的看着老师硬生生把一黑板公式算成了一个数字):
为避免出现(同理可得……中间过程省略……)这种情况,这里有必要简单的科普一下随机过程。放心,木有数学公式……
随机比较好理解,比如就说丢骰子吧,如果没有特别的情况,六个面出现的概率应该是一样的,也就是说,会随机出现1-6这六个数字中的一个:
那么一个人,丢出一次,只能得到这六个点数中的任意一个……出现的点数,实际上就一个随机值。但是如果有很多人,不停的丢骰子,那么每个人在投出的那一个瞬间,都会得到这六个点数中的任意一个。
但是,不管怎么丢,都有以下几个必然的情况:
1、任何人,在任何时候,丢出一个骰子,只能获得一个点数。(统计学里面,把这个叫做样本)
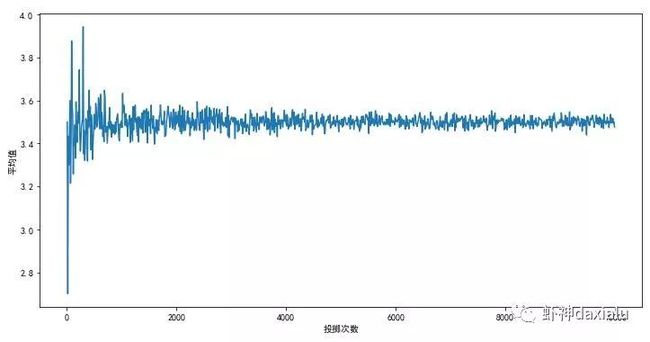
2、如对所有的点数,做出一个平均值,那么这个平均值应该是3.5附近,次数越多,就越接近3.5……(这个在统计学上叫做数学期望)。
那么随机过程又是什么呢?我们把丢骰子的时间(或者手法,或者其他的)当成一个参数,丢出的点数当成一个结果,这样就变成了一个函数:
从这个函数,我们就可以得到,随着时间的变化,你可以得到无穷多个随机的样本……but:他们又是有关系的,随着样本数量的增加,他们的数学期望值会逐渐的收敛,也就是所,样本间的规律,实际上是有迹可循的。
经典统计学上的这个概念,在地统计学上一样通用,地统计学也是在大量的样本的基础上,通过研究样本之间的规律,来探索他们的分布规律,然后利用这些规律来进行预测。
地统计学不但有统计学的一面,还有空间统计的一面,最重要的就是所谓地理学第一定律:“万物皆相关,越近相关性越大”,所以地统计学认为,所有的样本都不是相互独立的,都是遵循了一定的规律相互关联的,且遵循随机过程的结果。
所以,划重点,要考:
![]()
![]()
![]()
![]()
![]()
随机过程
地统计学的目的之一,就是要研究对象的内在规律,并且利用这个规律进行预测。
第二个前提假设,就是正态分布:
正态分布——地统计学的前体条件。
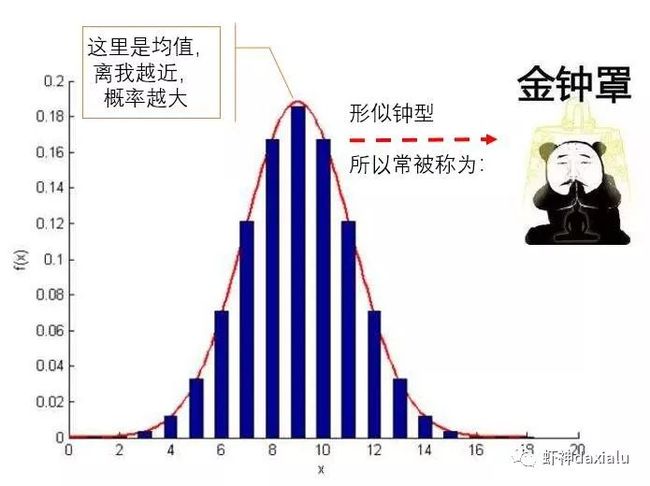
啥叫正态分布,就不用详细解释了吧:
正态分布的特点,就是随着样本的增加,观测值出现的概率,应该呈现出这种钟型曲线分布。
地统计学里面,要求样本是服从正态分布的,只要符合正态分布,后面才能够进行更好的进行分析研究,但是如果你的采样值不符合正态分布怎么办呢?
地统计学里面就给出了这样一个要求:当你的数据不符合正态分布的时候,需要对数据进行变换处理,尽可能选取可逆变换模型,将数据转换为符合正态分布假设的形式。
总之一句话:是正态分布要上,不是正态分布锤成正态分布也要上。
第三个前提假设,就是平稳性:
平稳性——地统计学的理论假设
地统计学认为,随机函数中的变量,在不同位置具有不同分布(善守者藏于九地之下——孙子,军形篇),且分布性质通常是未知的。所以仅仅靠着少量的钻孔获取到的样本值,很难用以来推断随机函数的整体分布。所以,就有必要对随机函数给出一些假设。
第一个假设,就是数据具有平稳性。
这里的平稳性一共有两种:
第一种是均值平稳性,是假设一组观测值的均值是不变的,并且与他们出现的位置无关,通俗说起来就是:将一批点集从一处移动到另外一处时,随机函数的性质保持不变。即随机函数的分布规律不会因为位置的改变而发生改变,具有严格的平稳性。
第二种就是与协方差函数有关的二阶平稳性以及半变异函数有关的内蕴平稳性。
所谓的二阶平稳性假设,就是认为随机函数的均值是一个常数,任意两个随机变量之间的协方差依赖的只是他们之间的距离和方向,与确切位置无关:
以上三个概念就是地统计学的前提假设,具体的数学公式,请大家去查阅相关资料……
下期预告:区域化变量的概念及性质,区域化变化是地统计学的数据基础。
待续未完。