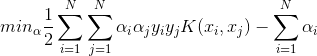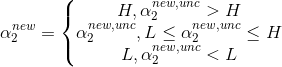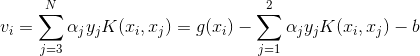SVM求解_SMO 机器学习
前言：
SMO 是求解SVM的一种算法(顺序最小化算法)sequential minimal optimization ，由1998年Platt提出。
主要解如下凸二次规划对偶问题：
求解过程中 里面关于二次规划算法收敛性证明，看了很多文档一直没找到。
目录：
- SMO简介
- 二次规划解析方法
- 变量选择方法
- SMO 算法
- 例子
一 SMO简介
SMO是一种启发式算法：
如果所有的变量满足KKT条件，最优化问题的解就得到了。
否则选择两个变量，固定其它变量，针对这两个变量构建一个二次规划问题。
整个SMO算法包括两个部分：
a 求解二次规划的解析方法
b 选择变量的启发方法
二 二次规划解析
SMO 求解的子问题为：
首先分析约束条件，在满足约束条件下，求解极小值
假设初始可行解为
,最优解为
,其中
因为：
2.1 当 
，根据![\alpha_1^{new} \in [0,C]](http://img.e-com-net.com/image/info8/46e10f0bd95d4797b355fff9ca973faa.gif){kind=small}
则： 
2.2 当 
则 
为了计算方便，记
定理1：
沿着约束方向，未经剪辑的解是
其中：
经过剪辑后 
的解是：
接着求
证明：
引入记号
目标函数可写成：
因为:
得到关于的目标函数：
对 求导：
:
带入 
得到
三 变量的选择
3.1 第一个变量选择（外层循环）
选取违反KKT最严重的样本点，并将其对应的变量作为第一个变量
其中：
3.2 第二个变量选择（内层循环）
选择 
最大的
3.3 计算阀值b 和差值 
...................1
因为：
带入1：
同理
如果 
如果 是0 或者C, 选择它们的中点作为
四 SMO算法
输入：
训练数据集
精度
C: 参数上限
输出： 
；；；；；；；；；；；；；流程；；；；；；；；；；；；；；；；；；；；
- 取初始值
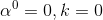, k 代表迭代次数 - 选取优化变量
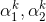, 解析求解两个变量的最优化问题, 得到新的
3 若在精度 满足停止条件
转4，否则令k=k+1,转2
4 
五 例子：
高斯核
线性核
CODE
# -*- coding: utf-8 -*-
"""
Created on Wed Nov 20 17:03:44 2019
@author: chengxf2
"""
import numpy as np
import os
import matplotlib.pyplot as plt
class SVM:
def DrawPot(self):
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(self.m):
x1 = self.dataMat[i,0]
x2 = self.dataMat[i,1]
label = self.labelMat[i,0]
if i in self.svIndex:
if label == -1:
ax.scatter(x1, x2, c = 'red' ,marker= 'o',s=80)
else:
ax.scatter(x1, x2, c = 'green' , marker= 's',s=80)
else:
ax.scatter(x1, x2, c ='black', marker= 'x',s=10)
plt.xlabel("x1")
plt.ylabel("x2")
plt.show()
"""
核函数
Args
dataMat: 数据集
z: 样本
return
k: 核函数
"""
def Kernel(self, dataMat, z):
m,n = np.shape(dataMat)
k = np.mat(np.zeros((m, 1)))
key = self.opt[0]
para = self.opt[1]
#print("\n key : ",key)
if "linear"==key:
k = dataMat*z.T
elif "Gauss"==key:
for j in range(m):
x = dataMat[j,:]
# print("\n x: ",x)
delta = x-z
k[j]=delta*delta.T
sigma = -para**2
k = np.exp(k/sigma)
else:
raise NameError("Error")
return k
"""
加载数据集
Args
None
return
None
"""
def LoadData(self):
file = open(self.path)
lines = file.readlines()
data = []
label =[]
for line in lines:
arr = line.strip().split('\t')
data.append([float(arr[0]),float(arr[1])])
label.append(float(arr[2]))
self.labelMat =np.mat(label).T # 标签集 #100 *1
self.dataMat = np.mat(data) ##数据集
self.m, self.n = np.shape(self.dataMat)
self.alpha = np.mat(np.zeros((self.m,1))) #拉格朗日乘子
self.eCache = np.mat(np.zeros((self.m,2))) ##[0,Ei]， 第一位是标志位（0,1),第二位是Ei: g(xi)-yi
self.KMat = np.mat(np.zeros((self.m, self.m))) ##Gram矩阵,核函数
for i in range(self.m):
self.KMat[:,i] = self.Kernel(self.dataMat, self.dataMat[i,:])
#print("\n 核函数： \n",self.k)
"""
计算当前预测值和实际值的差别
Args
i: 样本点
return
Ei: 预测值和实际值的差
"""
def CalcE(self, i):
para = np.multiply(self.alpha, self.labelMat).T*self.KMat[:,i] ##(m,1)
#print("para ",para)
gx = float(para+self.b)
ei = gx - self.labelMat[i,0]
#print("\n ",ei)
return ei
"""
产生一个不同于i的值
Args
i: 当前的i
return
j
"""
def RandJ(self, i):
j = i
while(j==i):
j = np.random.uniform(0,self.m)
return int(j)
"""
选择J
Args
i: 样本点
Ei: 差值
return
j: 对应的alphaJ
Ej: 对应的差值
"""
def ChooseJ(self, i, Ei):
maxJ = -1; maxDiff = 0.0; Ej = 0.0;
self.eCache[i]=[1,Ei]
eList = np.nonzero(self.eCache[:,0].A)[0]
n = len(eList)
if n>1: ###循环1
for e in eList:
if e == i:
continue
Ek = self.CalcE(e)
diffE = abs(Ei-Ek)
if diffE>maxDiff:
maxDiff = diffE; maxJ = e; Ej = Ek
return maxJ, Ej ######***********************************逻辑差一点
else:
j = self.RandJ(i)
Ej = self.CalcE(j)
return j, Ej
"""
编辑参数
Args
aj: 参数
H: 上限
L : 下限
return
aj: 剪辑过的参数
"""
def ClipAlpha(self, aj, H, L):
if aj>H:
aj = H
elif aj u=(0,c),tol = 0, 则xi落在间隔边界上,yg-1 = 0=> yEi = 0
2: 当alpha = C=>u=0, yg-1+tol=0 =>yEi+tol = 0，只能落在分离平面和间隔边界间，
3: 当 alpha =0=> u=C, tol =0 : yg>=1 => yEi>=0
"""
def VolidataKKT(self, i, Ei):
ZERO = 1e-3
"""
bKKT = ((self.labelMat[i,0]*Ei<-self.tol) and (self.alpha[i,0]self.tol) and (self.alpha[i,0]>0))
"""
label = self.labelMat[i,0]
if self.alpha[i,0]>0 and self.alpha[i,0]ZERO:
return True
else:
return False
if abs(self.alpha[i,0]-self.c)<=ZERO: ## alpha =c,ui=0,yg-1+tol=0 落在支撑平面内 yg <=1
if abs(label*Ei+self.tol)>ZERO:
return True
else:
return False
if abs(self.alpha[i,0])=1 就可以了
if label*Ei=0:
return 0
self.alpha[j]-= self.labelMat[j,0]*(Ei-Ej)/eta
self.alpha[j]= self.ClipAlpha(self.alpha[j,0],H,L)
self.SaveE(j)
if abs(self.alpha[j,0]-JOld)<1e-5:
return 0
self.alpha[i] +=self.labelMat[i,0]*self.labelMat[j,0]*(JOld- self.alpha[j,0])
self.SaveE(i)
b1 = -Ei- self.labelMat[i]*self.KMat[i,i]*(self.alpha[i]-IOld)-self.labelMat[j]*self.KMat[i,j]*(self.alpha[j]-JOld)+self.b
b2 = -Ej- self.labelMat[i]*self.KMat[i,j]*(self.alpha[i]-IOld)-self.labelMat[j]*self.KMat[j,j]*(self.alpha[j]-JOld)+self.b
if (self.alpha[i]>0 and self.alpha[i]0 and self.alpha[j]0) or entireFlag):
alphaPairsChanged = 0
if entireFlag :
for i in range(self.m):
alphaPairsChanged +=self.InnerLoop(i)
step +=1
else:
nonBoundIs = np.nonzero((self.alpha.A>0)*(self.alpha.A0)*(self.alpha.A
参考文档
《机器学习与应用》
《统计学习方法》