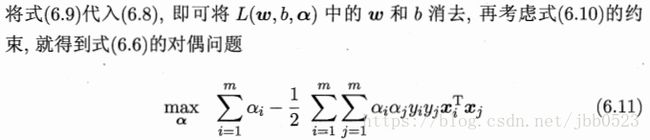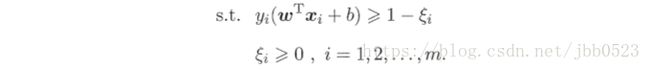由LIBSVM的svmtrain输出结果得到分类超平面的法向量w和偏移项b
题目:由LIBSVM的svmtrain输出结果得到分类超平面的法向量w和偏移项b
相信很多人都会使用LIBSVM软件包,svmtrain和svmpredict两个函数分别完成训练和预测:svmtrain输出训练模型,然将将训练模型作为svmpredict的输入参数即可得预测结果。训练模型作为一个中间变量似乎从来没有出现过,但对于很多人来说这的确已经足够了;然而,这并不能满足我们在某些应用场景的需要。SVM本质上与Logistic Regression一样,是训练得到一个分类超平面,有时候我们不仅仅是想要一个输出结果,而是要得到这个超平面,即法向量w和偏移项b,这时候就需要对svmtrain的输出模型进行研究了。
本文主要针对Matlab环境下应用LIBSVM,本文中的代码假设你已经下载并编译了LIBSVM,在文件夹中包含以下三个文件(本人为64软件,所以是.mexw64):
libsvmread.mexw64
svmtrain.mexw64
svmpredict.mexw64
还包含了以下数据集(该数据集在LIBSVM压缩包根目录下,无扩展名):
heart_scale
注:LIBSVM主页https://www.csie.ntu.edu.tw/~cjlin/libsvm/,请下载MATLAB and OCTAVE版本,目前最新版本是version3.22:
鉴于要读懂svmtrain的输出还是需要一些SVM的基础知道的,这里以[周志华. 机器学习. 清华大学出版社,2016.](以下统称西瓜书)为基础,原则上本文认为你已经读懂了第6章前四节内容,以下第1部分的有关支持向量机的介绍仅为第2部分介绍程序时叙述方便,详细内容请看原文。西瓜书必将成为机器学习领域的中文经典教材,建议买一本学习或者收藏,如果仅为了配合看本文也可以在网上搜索pdf电子版。以下为正文。
1、支持向量机基础
本部分重点知道分类超平面法向量w的计算公式(6.9)(或(6.17),二者相同),知道分类超平面偏移项b的计算公式(6.17)(6.18)即可,另外了解α是个什么角色……
支持向量机本质上是在某种约束条件下寻找一个分类超平面将正反两类样本分开:
支持向量机的模型是一个凸二次规划问题:
但一般是通过拉格朗日乘子法来求解而不用现成的优化计算包:
【敲黑板!!!】式(6.9)是重点!重点!!重点!!!
【敲黑板!!!】式(6.9)的用处来了:将解出的α代入即可得w。
【敲黑板!!!】式(6.17)和式(6.18)是重点!重点!!重点!!!
然而以上介绍的是硬间隔支持向量机,即没样训练样本违反式(6.6)的约束条件,也就是说训练样本在样本空间或特征空间是线性可分的,即存在一个超平面能将不同类的样本完全分开。然而现实中这种情况过于理想化,更为实际的方法是允许一些样本违反式(6.6)的约束条件,因此有了软间隔(Soft Margin)支持向量机,优化目标如下:
该优化问题一般仍采用拉格朗日乘子法求解:
注意,式(6.37)与式(6.9)一模一样。求解优化问题式(6.40)解出的α,求出w和b即可得到划分超平面。法向量w可以通过式(6.37)求解,b仍通过式(6.17)或更鲁棒的式(6.18)来求解,但这里有个特别要注意的问题:式(6.17)成立的前提是支持向量在最大间隔边界上,这对于硬间隔支持向量机来说没啥问题,所有支持向量都在最大间隔边界上;但对于软间隔支持向量机来说只有满足0<αi
2、MATLAB例子代码及解释
代码如下(需要libsvmread,svmtrain, svmpredict三个.mexw64文件以及heart_scale数据集,heart_scale在libsvm-3.22.zip解压后根目录下,三个.mexw64文件是编译根目录matlab文件夹内的文件所得):
%libsvm中间参数探索@20180704
clear all;close all;clc;
[y, x] = libsvmread('heart_scale');
x = full(x);
%SVM训练
model = svmtrain(y, x, '-t 0 -c 1');
[predict_label, accuracy, dec_values] = svmpredict(y, x, model);
%支持向量索引(Support Vectors Index)
SVs_idx = model.sv_indices;
%支持向量特征属性和类别属性
x_SVs = x(SVs_idx,:);% or use: SVs=full(model.SVs);
y_SVs = y(SVs_idx);
%求平面w^T x + b = 0的法向量w
alpha_SVs = model.sv_coef;%实际是a_i*y_i
w = sum(diag(alpha_SVs)*x_SVs)';%即西瓜书公式(6.9)
%求平面w^T x + b = 0的偏移项b
%由于是软件隔支持向量机,所以先找出正好在最大间隔边界上的支持向量
SVs_on = (abs(alpha_SVs)<1);%C=1 by parameter '-c 1'
y_SVs_on = y_SVs(SVs_on,:);
x_SVs_on = x_SVs(SVs_on,:);
%理论上可选取任意在最大间隔边界上的支持向量通过求解西瓜书式(6.17)获得b
b_temp = zeros(1,sum(SVs_on));%所有的b
for idx=1:sum(SVs_on)
b_temp(idx) = 1/y_SVs_on(idx)-x_SVs_on(idx,:)*w;
end
b = mean(b_temp);%更鲁棒的做法是使用所有支持向量求解的平均值
%将手动计算出的偏移项b与svmtrain给出的偏移项b对比
b_model = -model.rho;%model中的rho为-b
b-b_model
%将手动计算出的决策值与svmpredict输出的决策值对比
%决策值f(x)=w^T x + b
f_x = x * w + b;
sum(abs(f_x-dec_values))运行以上程序,输出两个非常小的值。第1个值很小说明我们手动计算出来b与model中给出的b相差很小;第2值很小说明我们手动计算出w和b后根据式(6.12)得到的决策值与svmpredict输出的决策值基本一致。
以下简单介绍一下程序中的几个关键点。
以上三行是实现SVM的训练和预测。这里svm通过’-t 0’设置为线性核,值得注意的是这里也必须设置为线性核,否则根据西瓜书6.3节的内容,w对应的应该是映射后的特征向量φ(x),若为高斯核(RBF核)则φ(x)为无穷维向量,即w也为无穷维向量,为了避免高维计算,此时一般不显式计算w,而是使用核函数,如西瓜书式(6.24)所示一样计算决策值f(x),此即核技巧。
以上三行是为了实现西瓜书式(6.9)得到w。对于式(6.9)来说,若xi不是特征向量则相应的αi等于0,即不出现在式(6.9)中;因此式(6.9)相当于将每个支持向量xi乘以对应的系数αiyi后累加得到法向量w,维度与xi相同。
以上10行是为了实现西瓜书式(6.18)得到b。其中第23~25行是找出位于最大间隔边界上的支持向量,第23行之所以取abs(alpha_SVs) 是由于alpha_SVs中包含了y_i,因此要取绝对值,而(abs(alpha_SVs)<1)中的小于1是由于式(6.35)中的C=1,这是在第7行中通过'-c 1'实现的;第28~30行实际是针对每一个位于最大间隔边界的支持向量求了一个b,即式(6.18)中括号之内的表达式;第31行取平均即为式(6.18)。
另外,b_temp的最大值为1.0502,最小值为1.0512,平均值为1.0507,可见只要是在最大间隔边界上的支持向量计算出的b差别很小,当然使用平均值仍是比较鲁棒的方法。
有关svmtrain的输出model结构体内各变量的含义参见《libsvm 训练后的模型参数讲解》(链接:http://blog.sina.com.cn/s/blog_6646924501018fqc.html),简单摘抄如下以做备份:
model.Parameters参数意义从上到下依次为:
-s svm类型:SVM设置类型(默认0)
-t 核函数类型:核函数设置类型(本例设为0即线性核,参见西瓜书6.3节)
-d (degree):核函数中的degree设置(针对多项式核函数)(默认3)
-g (gama):核函数中的gamma函数设置(针对多项式/rbf/sigmoid核函数) (默认特征属笥数目的倒数,本例中为1/13)
-r coef0:核函数中的coef0设置(针对多项式/sigmoid核函数)((默认0)
model.nr_class表示数据集中有多少类别,本例为二分类;
model.totalSV表示支持向量的总个数,本例共有101个;
model.rho是分类超平面的偏移项的相反数(即-b);
model.Label表示数据集中类别的标记都有什么,这里是1和-1,对应于nr_class;
model.indices表示支持向量在训练集中的索引,即第几个训练样本为支持向量,是一个大小为totalSV的列向量;
model.ProbA
model.ProbB这两个参数使用-b参数时才能用到,用于概率估计;
model.nSV表示每类样本的支持向量的数目,这里表示标记为1的样本的支持向量有51个,标记为-1的样本的支持向量为50;(注意:这里nSV所代表标记的顺序与Label对应)
model.sv_coef表示式(6.9)(或(6.37))中支持向量的αiyi(因为非支持向量αi=0),是一个大小为totalSV的列向量;;
model.SVs表示所有支持向量,以稀疏格式存储,若要转为普通矩阵可使用函数full;
有关svmpredict函数的三个输出,第1个predict_label为预测结果标记,第3个 dec_values为决策值(即式(6.12)中的f(x)),第2个accuracy包含三个结果,依次意义分别是:分类准率(分类问题中用到的参数指标)、平均平方误差MSE (mean squared error)[回归问题中用到的参数指标]、平方相关系数r2(squared correlation coefficient)[回归问题中用到的参数指标]
本例中仅以二分类为例说明,若数据集为多分类则会与此说明不同,暂时到此。
【更新@20191202】若将LIBSVM用于多分类场景,会采用One vs One(OvO)分解方式求解,各OvO 分解超平面的w和b求解参见以下博客:
《将LIBSVM用于多分类时根据svmtrain输出结果得到各OvO分类超平面的法向量w和偏移项b》
链接:https://blog.csdn.net/jbb0523/article/details/103355415
参考文献:
[1]LIBSVM:https://www.csie.ntu.edu.tw/~cjlin/libsvm/
[2]周志华. 机器学习. 清华大学出版社,2016.
[3] libsvm 训练后的模型参数讲解,http://blog.sina.com.cn/s/blog_6646924501018fqc.html