The Elements of Statistical Learning-线性模型和最小二乘法（5）

考虑到整理的方便，后面每一个章节都放在一个文件中，然后想到哪写到哪

线性模型和最小二乘法

Input vector: XT=(X1,X2,…,Xp) X T = ( X 1 , X 2 , … , X p )

Predict Output: Y Y

By the linear regression model:

f(X)=β0+∑j=1pXjβj f ( X ) = β 0 + ∑ j = 1 p X j β j

Assumes regression function E(Y|X) E ( Y | X ) is linear or reasonable approximation.

Xj X j can come from difference sources.

Least squares estimation, the residual sum of squares:

RSS(β)=∑i=1N(yi−f(xi))2=∑i=1N(yi−β0−∑j=1pxijβj)(71)(72) (71) R S S ( β ) = ∑ i = 1 N ( y i − f ( x i ) ) 2 (72) = ∑ i = 1 N ( y i − β 0 − ∑ j = 1 p x i j β j )

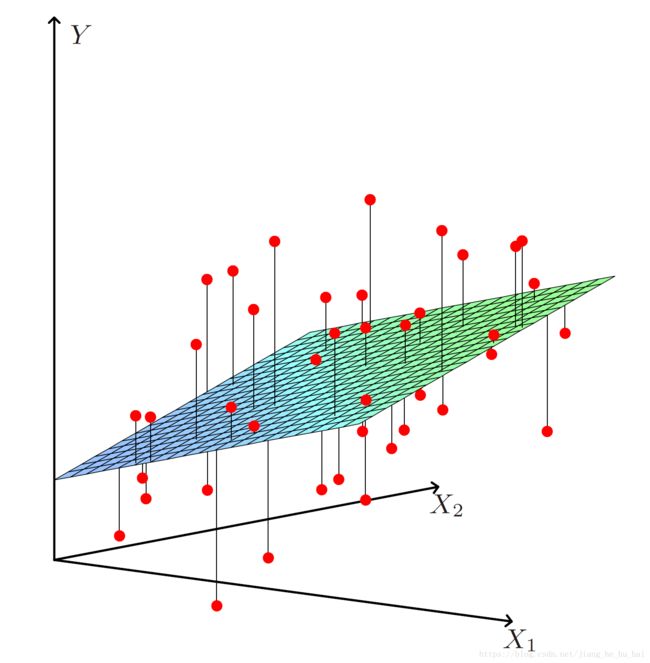
把RSS写成矩阵形式就是

RSS(β)=(y−Xβ)T((y−Xβ)) R S S ( β ) = ( y − X β ) T ( ( y − X β ) )

很容易计算其最小值点： β^=(XTX)−1XTy β ^ = ( X T X ) − 1 X T y
下图可以看出，计算最小二乘的几何意义就是相当于在黄色低维超平面上找一个向量 y^ y ^ 来近似原来的向量 y y ，很显然在 y−y^ y − y ^ 与黄色低维超平面垂直的时候 y^ y ^ 与 y y 最近。

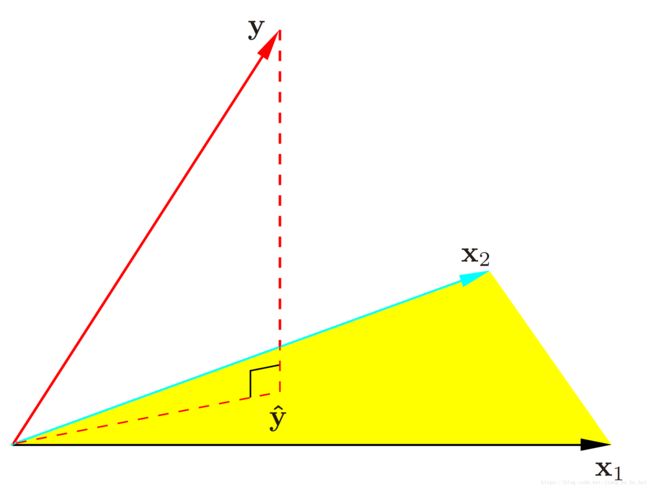
因此，我们又可以得出预测值与真实之的关系：

y^=Xβ^=X(XTX)−1XTy=Hy y ^ = X β ^ = X ( X T X ) − 1 X T y = H y

The matrix H H sometimes called the “hat” matrix OR projection matrix, because it puts the hat on y y .
如果这里 y y 是独立的，并且方差(或者协方差)为常值 σ2 σ 2 ，我们很容易就能计算出 β^ β ^ 的方差。

为了表示方便，这里仅仅用 ² 表示乘以自身转置。

Var(β^)=E(β^−Eβ^)(β^−Eβ^)T=E((XTX)−1XTy−E((XTX)−1XTy))2=[(XTX)−1XT][(XTX)−1XT]TE(y−EY)2=(XTX)−1σ2 V a r ( β ^ ) = E ( β ^ − E β ^ ) ( β ^ − E β ^ ) T = E ( ( X T X ) − 1 X T y − E ( ( X T X ) − 1 X T y ) ) 2 = [ ( X T X ) − 1 X T ] [ ( X T X ) − 1 X T ] T E ( y − E Y ) 2 = ( X T X ) − 1 σ 2

可以由下面的式子来估计 σ2 σ 2 :

σ^2=1N−p−1∑i=1N(yi−y^i)2 σ ^ 2 = 1 N − p − 1 ∑ i = 1 N ( y i − y ^ i ) 2

这里分母去 N−p−1 N − p − 1 而不是 N N 可以参考下面以为形式的证明：


这里如果 σ^2 σ ^ 2 是 σ2 σ 2 的一个无偏估计就有 E(σ^2)=σ2 E ( σ ^ 2 ) = σ 2 ，证明参考 这里的方差偏差分解公式的推导。

如果我们假设 f(X)=β0+∑pj=1Xjβj f ( X ) = β 0 + ∑ j = 1 p X j β j 是对 Y Y 的均值的正确估计，再假设 Y Y 的离散在其期望周围是可加和高斯的。也就是说：

Y=E(Y|X1,…,X−++p)+ε=β0+∑j=1pXjβj+ε Y = E ( Y | X 1 , … , X − + + p ) + ε = β 0 + ∑ j = 1 p X j β j + ε

其中 ε∼N(0,σ2) ε ∼ N ( 0 , σ 2 )
结合上面的结论，我们就可以得到

β^∼N(β,(XT,X)−1σ2) β ^ ∼ N ( β , ( X T , X ) − 1 σ 2 )