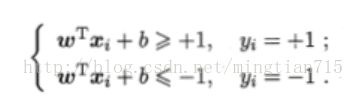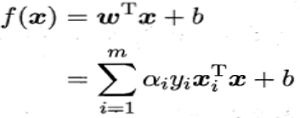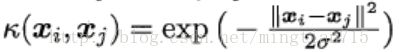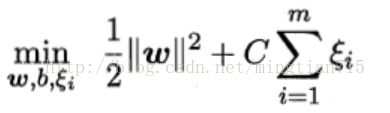支持向量机SVM
支持向量机由于其优异的性能,在机器学习中与神经网络共享美誉。
支持向量机的前身是最优间隔分类问题,在后者基础上加上核函数,便摇身一变为了SVM。
本文参考周志华《机器学习》以及吴恩达网易公开课《机器学习》
问题描述
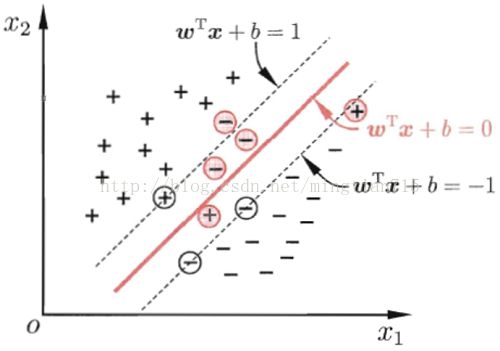
给定训练样本训练集D={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{-1,+1},分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面,将不同类别样本分开,如下图所示。
超平面很多,应该如何选取呢?直观来看,应该去找位于两类训练样本“正中间”的划分超平面,即上图中加粗的那个,因为该划分超平面使得对训练数据样本局部扰动的“容忍”性最好。最大化间隔,并限制训练样本数据(+例,-例)都与超平面的距离大于该间隔。
假设由(w,b)确定的超平面能将训练样本正确分类,即对于(xi,yi)∈D,若yi=+1,我们希望z = wx+b>0,即会有sigmoid(z)>0.5,为正例概率大于0.5;反之,若yi=-1,我们希望z =wx+b<0,即会有simoid(z)<0.5,为反例的概率大于0.5。令:
用图来描述上式,就是:
因此,为了最大化间隔(2/||w||),等价于最小化||w||,于是就有了支持向量机(SVM)的基本型:
对偶问题
SVM基本型本身就是一个凸二次规划问题,能直接用现成的优化计算包求解,但是有更高效的方法。
使用拉格朗日乘子法,引入拉格朗日乘子α>=0,则拉格朗日函数为:
下面引入“对偶问题”
因此,求解原问题的对偶问题可得到原问题的下界,若等号成立,则对偶问题和原问题同时得到解决,此时满足KKT互补条件(KKT条件基础上加了一些限制),称为强对偶。
求解对偶问题,需要对w,b求偏导数为0,得到:
得到模型:
约束条件:
从约束条件可以看出,当α=0时,不会对f(x)有影响,当α>0时,要求yif(xi) = 1,即函数间隔为1,所对应的样本点位于最大间隔边界上,是一个支持向量。这表明:训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关。
核函数
设原变量为x,为了使其线性可分,可能要映射到更高维空间,其表示为Φ(x),核函数的定义即:
核函数的意义很明确,就是不用直接计算<Φ(xi),Φ(xj)>,因为Φ(x)是将x扩展到了n维空间(x.^n的线性组合),计算起来是十分麻烦的。核函数定义有着抽象,下面举个具体例子,很好理解:
这个例子很好的说明了核函数的高效性,当n很大时,节省了大量的计算时间,此例中k(x,z)其实就是常用核之一的多项式核函数。
此外,还有一种理解核函数直观的方法。我们用核函数取代<Φ(xj),Φ(xj)>,即两个向量的内积,当这俩个向量方向相同时,表明其相似度高,其内积结果大(不考虑模的大小);若方向不同,则内积结果较小,相似度较低。
因此x,z相似度较高时,核函数k(x,z)应该较大,x,z相似度较低时,k(x,z)应该较小。这种方式不是很准确,但是比较直观,以这种方式可以理解高斯核函数:
实际上,对核函数k判定有效性有很直接的方法,就是判定"核矩阵"K是否半正定:
若K为半正定矩阵,则核函数k是有效的。
下面是常用核函数:
核函数的存在使得SVM算法非常高效。此外,核函数的应用十分广泛,例如线性回归,对数回归等,只要可以将算法写成内积
软间隔
软间隔的概念比较好理解,其实就是因为现实任务中往往很难找到合适的核函数使得样本线性可分,即使找到,可能因为函数间隔太小,数据的轻微扰动都会带来不同的划分结果(过拟合)。如下图所示:
因此,为了解决这个问题,可以适当允许某些样例划分错误,同时引入代价函数控制这种划分错误的数量。此时问题描述为:
其中ξi代表了划分情况,如果ξ=0则间隔函数大于等于1,与之前划分结果相同,若0<ξ<1则说明其距离超平面距离小于1,若ξ>1则出现了划分结果错误的现象。
这也是一个二次规划问题,类似之前的求解过程,可转换为对偶问题:
与之前“硬间隔”问题相对比,只是有了α小于C的限制。其实硬间隔也可以这么写,只是对应C=+无穷,从惩罚函数的效果来看就是不允许任何错误结果。
当α=0时,对应距离大于1的样本;当α=c时,对应软间隔的样本;当0<α
SMO算法
SMO算法是一种非常高效的求解算法,用来求解对偶问题W(α1α2..αm)。
其由坐标上升法演变而来,即每次只改变一个变量,保持剩余变量不变,使得目标函数增大或减小。相比牛顿法,更新过程更加简单,但迭代次数更多。
但由于SVM中有如下限制: