Spectral Clustering by Joint Spectral Embedding and Spectral Rotation

                 

orthonormal matrix

正交矩阵的定义

如果： 或  （则n阶实矩阵A称为正交矩阵）

正交矩阵的性质

1 是正交矩阵

2 A的各行是单位向量且两两正交

3 A的各列是单位向量且两两正交

4 |A|=1 或 -1

 

 

文章原文：

---

The existing joint model adopts  an orthonormal real matrix to approximate the orthogonal but  non-orthonormal cluster indicator matrix. It is noted that only  in a very special case (i.e., all clusters have the same number of samples), the cluster indicator matrix is an orthonormal matrix multiplied by a real number.

 

The error of approximating a non-orthonormal matrix is inevitably large. To overcome the drawback, we propose replacing the non-orthonormal cluster indicator matrix with a scaled cluster indicator matrix which is an orthonormal matrix.

---

现有的模型采用标准正交矩阵近似正交但非正交标准化的聚类指标矩阵，当且仅当所有类别中的结点数量一致的时候，才是标准正交矩阵(乘一个实数)，

这种方式的误差很大，为了解决这种问题，作者提出把非正交标准化的矩阵替换成一个标准正交化的 scaled cluster indicator matrix。

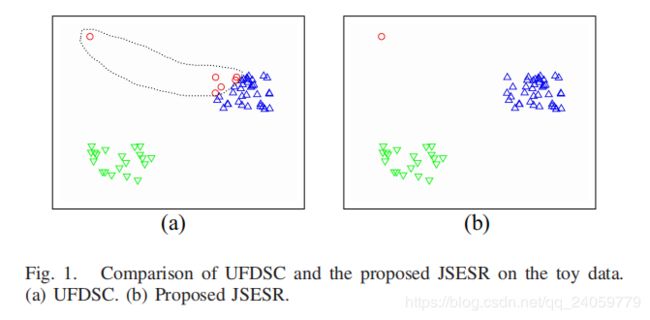
Yang et al. 在2016年IJCAI上面提的UFDSC方法也是一个联合学习模型，但是因为使用了正交标准化的约束，而使得最后的结果不准确，对于每个社团内节点数量相同的数据集可以有很好的效果，但是对于数据分布极其不均匀的数据集，UFDSC会不准确，给出了一个toy-example

左边UFDSC算法，红点的聚类数量少，加上正交标准化的限制，就会把其他社团的结点抓取过来，造成最后聚类结果的不准确。

 

1.A joint model is proposed to simultaneously and iteratively perform spectral embedding and spectral rotation with spectral embedding generating a real-valued cluster indicator matrix and spectral rotation generating a binary cluster indicator matrix. Compared to the classical spectral clustering methods, the proposed joint model is able to overcome the drawbacks of the information loss and the risk of the discrete clustering deviation.

2.In the spectral rotation part of the proposed joint model, approximation is conducted in-between two orthonormal matrices:a) a matrix generated by spectral embedding followed by a rotation operation and b) a scaled cluster indicator matrix. Therefore, the proposed method is able to obtain an accurate clustering result. In addition, the proposed method is able to overcome the problem of the unbalance of UFDSC.

3. The physical meaning of the scaled cluster indicator matrix is interpreted. Moreover, the theoretical derivation of the scaled cluster indicator matrix is given. The insight in the scaled cluster indicator matrix is helpful to understand the proposed method and developing a new method.

 

谱聚类，先使用

                                                                

构造图相似度矩阵， 然后构造图拉普拉斯矩阵，L=D-W，D是度矩阵，拉普拉斯矩阵有一些很好的性质

1）拉普拉斯矩阵是对称矩阵，因为D和W都是对称矩阵

2）由于拉普拉斯矩阵是对称矩阵，则它的所有特征值都是实数

3）对于任意向量，我们有

                                       

推导过程：

                                                  

                                             

原文使用的是 k-way N-cut,公式三：

The goal of minimum k-way Ncut is to simultaneously minimize the sum f(Y)

                                                                                

and maximize the sum g(Y) of weighted volume V(C_{k}) of each cluster C_{k}

                                                                                 

The effect of minimizing the sum of similarity is to let samples in different clusters have the least similarity

这里应该就开始省略定义，这里要求的变量是Y，Y中每一个列向量y_{i}代表着第i个节点的类别归属，对于任意给定的向量表示y_{i}和y_{j}，它们要受到原图的相似度矩阵A的限制，即满足

                                                              

                                                      

对于有k个类别来说：

                                                                  

同时考虑

                                                                 

Therefore,the problem of k-way Ncut can be formulated as minimizing J(Y)

                                                                    

                                              

                                                      

设 

则原式可以转化为：

                                             

Define  Then J(Z) can be rewritten as:

where   is known as the normalized Laplacian matrix. Note that  is hard to solve, because the elements of \hat{F} are constrained to be discrete values. The solution of this problem is to relax the matrix \hat{F} from discrte values to continuous ones. Then the problem J(\hat{F}) becomes 

 where 

其实上面就是一个N-way 的 Spectral embedding ：

 

Classical Spectral Rotation 

The optimal  which is obtained by soling the optimization problem above is not a zero-one valued matrix.

Therefore, to get the final clustering result, it is common to apply K-means or spectral rotation to transform F* to a zero-one value matrix so that it approaches the underlying cluster indicator matrix. It is known that the underlying cluster indicator matrix Y is binary and its element is either 0 or 1.

 

谱旋转的定义：

Spectral rotation is an algorithm for optimal transforming the real-valued cluster indicator matrix F* to a binary matrix Y.

首先，最优的解F*不是唯一的，对于任意的正交矩阵R^{T}R=I,都能够使得原矩阵有另一个最优解

简单的说就是用一个正交矩阵去重构最优解，使其与一个离散binary matrix之间最小化。

 

目标方程：

---

学习：该目标方程的优化，两个基于SVM，

算法的收敛性证明

实验部分使用的指标：

ACC NMI  PURITY   HOMOGENEITY   JACCARD INDEX

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

https://www.cnblogs.com/pinard/p/6221564.html