CS231n Lecture 15 | Efficient Methods and Hardware for Deep Learning
Lecture 15主要从算法和硬件两个层面讲解了模型压缩和优化等问题,以实现深度学习模型的体积减少、参数数量缩减、计算量减少、计算加速等。
文章目录
- Abstract
- Algorithms for Efficient Inference
- Pruning(剪枝)
- Weight sharing(共享权重)
- Quantization(量化)
- Low Rank Approximation(低秩近似)
- Binary / Ternary Net(二进制/三元网络)
- Winograd Transformation(Winograd变换)
- Hardware for Efficient Inference
- Algorithms for Efficient Training
- Parallelization(并行化)
- Mixed Precision with FP16 and FP32(16位浮点数和32位浮点数的混合精度)
- Model Distillation
- DSD: Dense-Sparse-Dense Training
- Hardware for Efficient Training
Abstract
降低能耗是很重要的,那么这些能量都消耗在哪了呢?
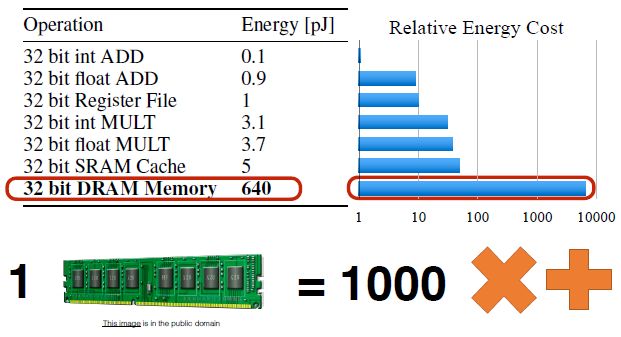
上图可以看到存储访问的耗能比数学运算的耗能高两到三个数量级,因此,我们需要将算法和硬件联动设计来实现效能的提升。
在此之前,我们先来将一些硬件的基础知识:
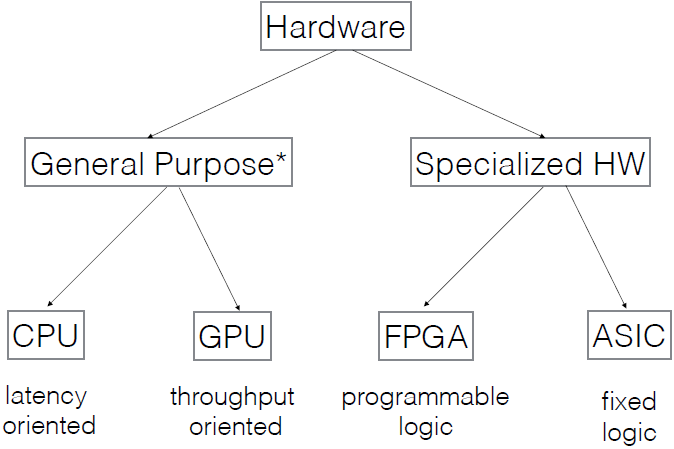
上图为硬件的组成。通用硬件中CPU是延时导向、单线程的,就像一头大象,而GPU是吞吐量导向的,有很多弱小的线程,虽然小,但是成千上万,就像一群蚂蚁。专用硬件中FPGA表示现场可编程门阵列,它是可编程硬件,逻辑性可以改变,但效率不高,介于通用硬件和ASIC之间。ASIC表示特定用途的集成电路,它有固定逻辑,为某种特定应用专门设计(如深度学习),Google的TPU就是一种ASIC。
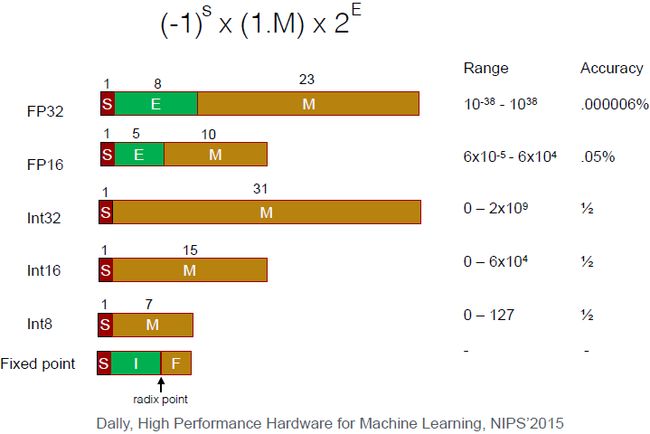
上图为计算机硬件中的数字表示。计算机中的数字都是离散的,如FP32,它由三个部分组成,符号位S,指数为E和尾数位M,这个FP32的数值等于上图顶部的公式计算结果。这里特别说一下int8(TPU使用的数据类型),用整数来表示一个定点数,这里有几位用来表示整数,如果用到了不同的层会跟一个小数点,最后几位用来表示小数部分。为何我们更喜欢8和16位,请看下图的计算开销。

从上图中我们可以看出,从32位到16位,能耗上我们节约了4倍,所占面积也降低了4倍。
Algorithms for Efficient Inference
Pruning(剪枝)
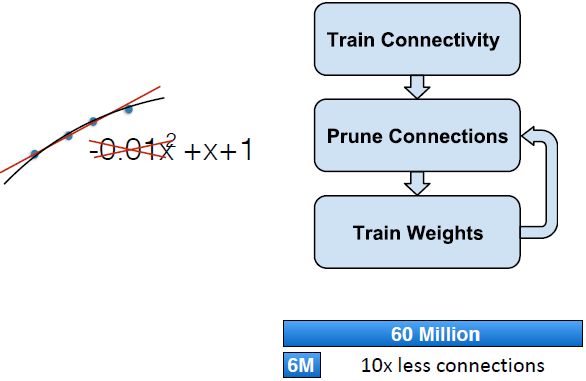
实际上不是所有的参数都是有用的,比如拟合一条直线,但你使用的是一个二次函数,那么二次项系数很明显就是一个多余的参数。
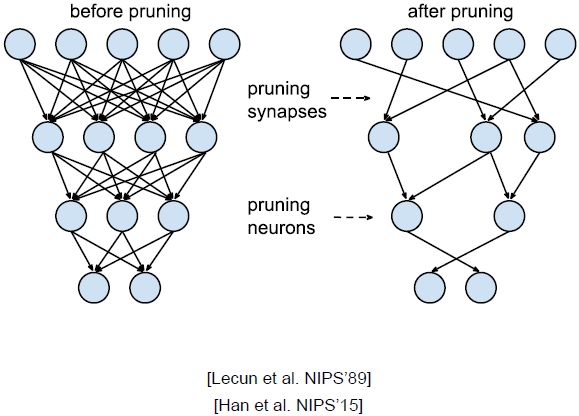
剪枝过程:首先训练神经网络,然后修剪一下连接(对权重大小进行排序,删掉小的权重),再训练剩下的权重,重复这样的过程进行迭代。结果就是我们将模型计算量缩小了十倍。
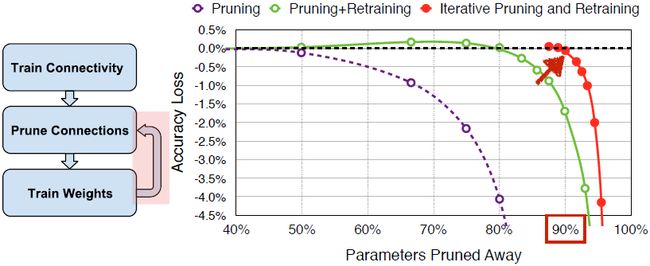
上图紫色曲线为原始模型的预测准确率,横轴为修剪了多少参数,纵轴表示模型的准确率。绿色曲线为我们重新训练剩下的权重后的准确率曲线,红色曲线为我们不断地进行裁剪与再训练后的准确率曲线。我们可以发现,裁剪了90%的参数后模型仍能回到最初的准确率。


由上述两幅图可以看出,裁剪与再训练对于RNN和LSTM也是有效的。上图可以看出当裁剪了95%的参数时,网络就开始出现问题了,因此这里存在着一个阈值。
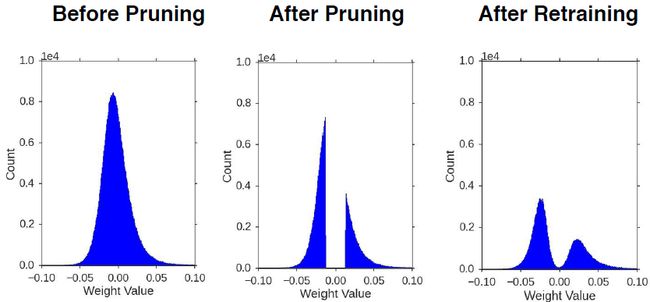
当然裁剪也改变了权重分布,因为我们剔除了小的连接点,之后我们重新训练,所以分布最终还是平滑的。
Weight sharing(共享权重)
现在通过剪枝,参数数量减少了,但我们希望每个参数有更少的位数,这样参数乘在一起后模型也会变小。
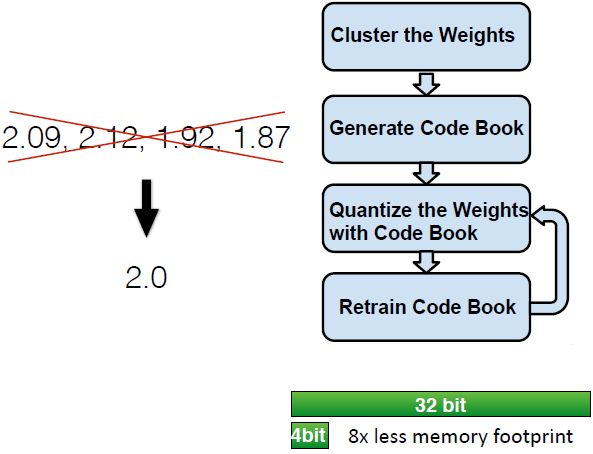
不是所有的权重都需要有准确的数值,太精确的数字只会导致过拟合。思路就是把所有权重聚类,用一个聚类质心来表示这些相近的数。
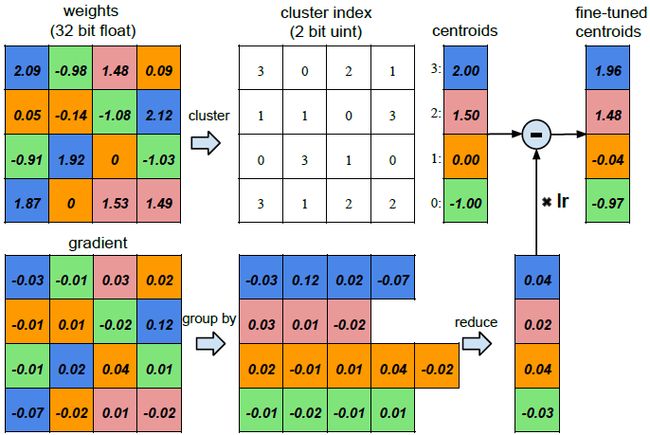
如上图是一个4x4权重矩阵,我们用kmeans对其进行聚类,将其分成四类,这样我们仅仅需要存储一个2位的类别号,而不是整个32位浮点数,缩小了16倍。
训练时将它们结合在一起,然后得到梯度,我们将相同聚类汇总的梯度求均值,然后乘以学习率再从原始的聚类质心汇总减去这个值。
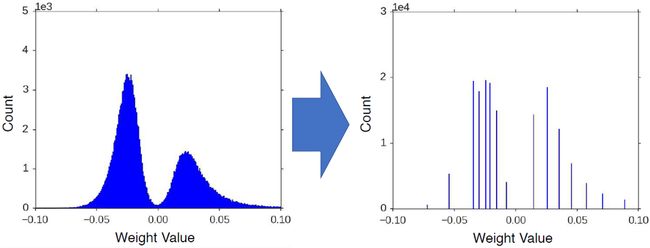
权值共享后,权重分布就变成离散的了。这里只有16个不同的值,一维着可以用4位来表示一个数。

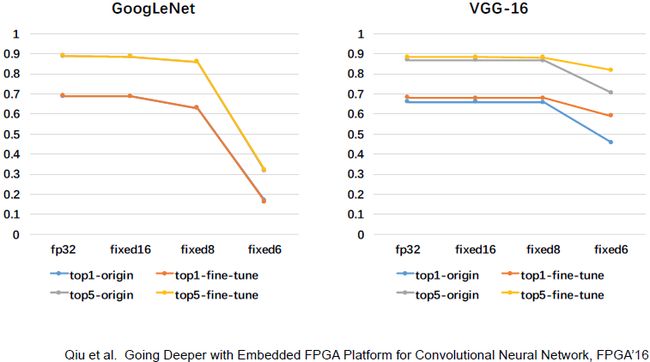
上图所示是我们给模型相应的数位后模型的准确率变化。我们可以发现卷积神经网络到4bit精度才开始下降,而全连接神经网络到2bit才开始下降。
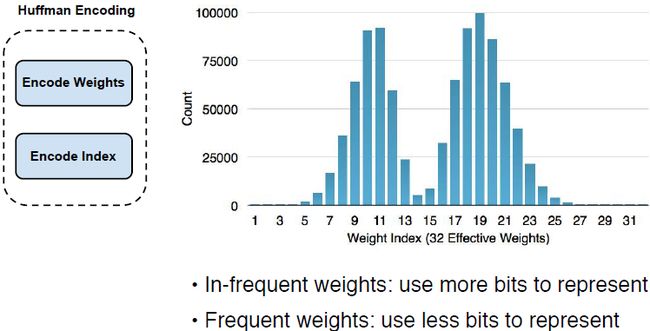
最后我们的想法是用哈夫曼编码来用更多的数位表示不常出现的权重,使用更少的数位来表示经常出现的权重。
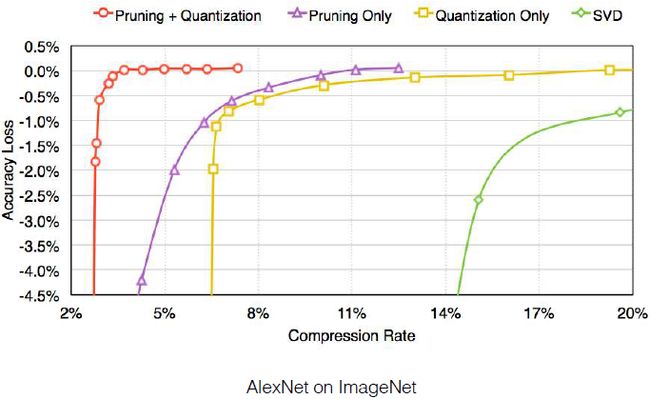
因此,综合上述方法,在不影响准确率的情况下,模型压缩情况如下图所示。
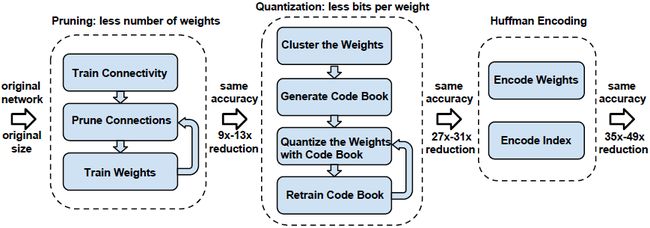

下一个问题是我们能不能直接搭建一个精简的模型,而不是对既有模型进行压缩呢?于是提出了SqueezeNet。

其想法是在3x3的卷积前先使用通道更少的层。这里有两个分支,而不是inception模型中的四个分支。此模型没有FC,最后一层是全局池化。
如果我们对SqueezeNet继续使用前述的压缩方法呢?

我们发现哪怕是压缩了510倍,SqueezeNet依然具有和AlexNet一样的准确率。
Quantization(量化)

用标准浮点数训练一个NN,通过收集每一层的统计信息,来量化权重和激活值(如最大最小值,均值,多少位数字能足以表示这个动态范围)。我们用这么多位表示整数部分,用剩下几位表示其他部分。我们也可以微调浮点数的格式,或者用定点数前向传播,用浮点数反向传播并更新权值。
Low Rank Approximation(低秩近似)
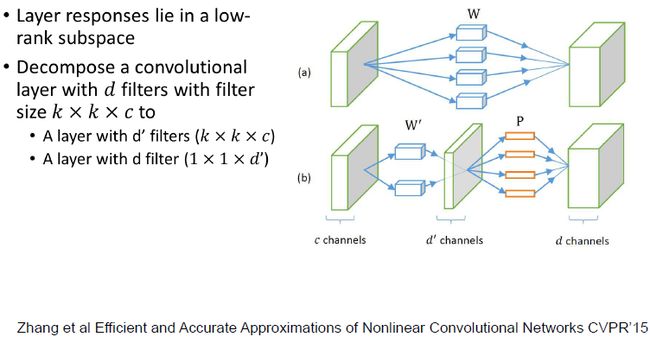
实践证明可以将一个CONV拆分成两部CONV,前面一个CONV后接一个1x1的CONV。

此方法同样适用于FC。最简单的想法是用SVD分解把一个矩阵拆成两个矩阵。
Binary / Ternary Net(二进制/三元网络)

我们看到了剪枝后的分布,权值有正有负,我们能否只用三个数1、-1、0来表示这个神经网络呢。

文章表明在训练时我们保留一个完全精准的权重,但在推断的时候仅保留尺度因子和三元权值,我们仅需要三个权重。
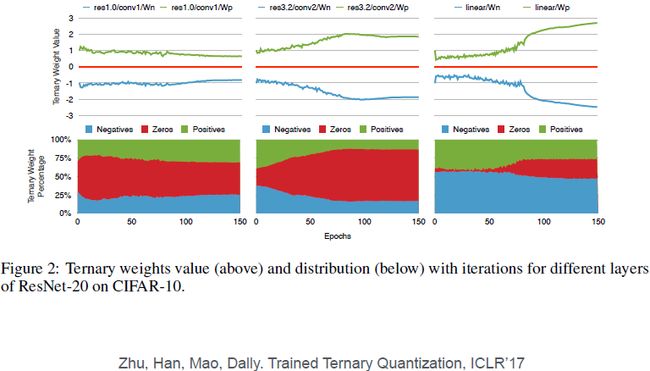
上图为正、零、负权重的比例,权值的符号和绝对值在训练过程中都会变化。

可看出在ImageNet测试集上测试的精度与其他方法几乎收敛在同样的地方。
Winograd Transformation(Winograd变换)
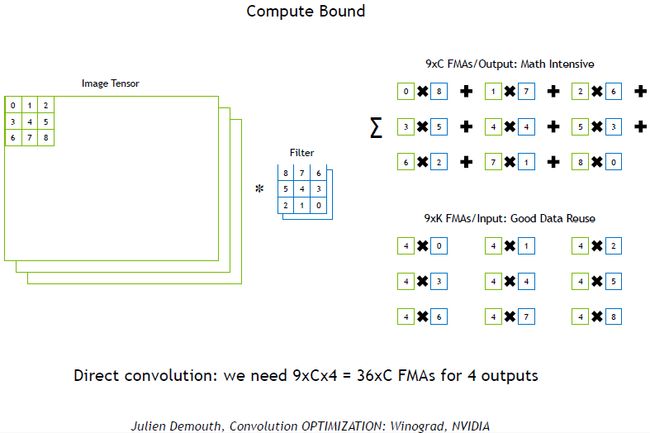
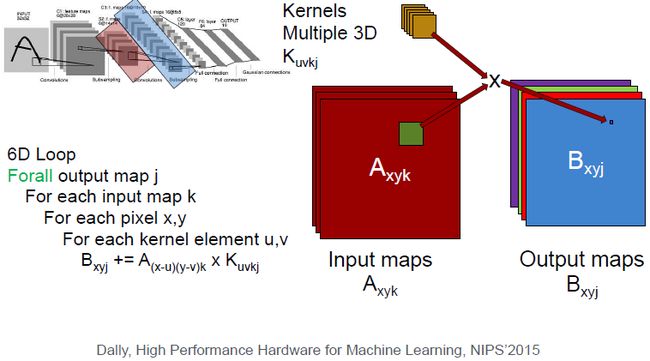
上图为正常的卷积步骤,最开始,我们只是做元素的点乘,对卷积核里的9个元素和图片上的9个元素进行点乘运算再求和。每得到一个输出,我们都需要进行 9 × C 9\times C 9×C次的乘法和加法运算。
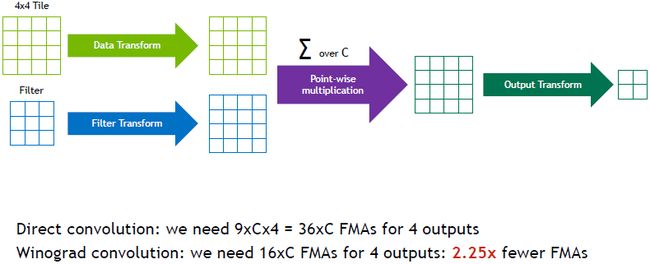
Winograd卷积是另外一种等价方法,此方法不是直接计算卷积而是一步一步移动,首先,将输入特征映射转换到另一个特征映射,这个映射只包含权重1、0.5、2,可以用移位有效实现。同时卷积核转换为 4 × 4 4\times4 4×4张量,然后做一个元素对元素的点乘,再将所有的c加起来,最后做一个逆变换得到四个输出。于是速度提升了2.25倍。
Hardware for Efficient Inference
Algorithms for Efficient Training
Parallelization(并行化)
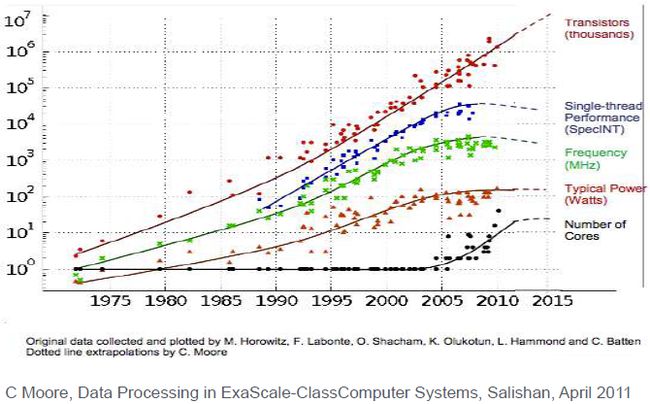
随着时间的推移,晶体管的数量在增加,但近年来单线程下的性能上升趋势进入瓶颈,芯片的频率也因为功率的约束不再提升。但是内核的数量在增加。

数据并行化。同时将两张图片读入模型同时处理,这需要权值之间协同更新。
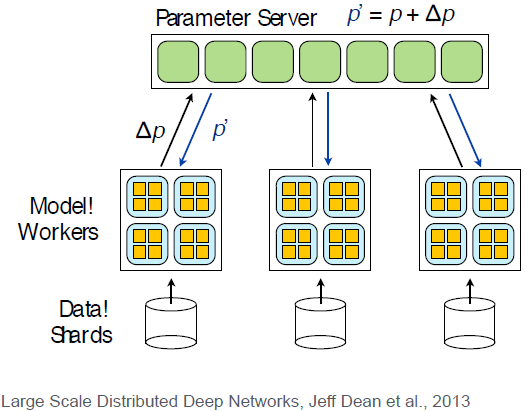
有一个参数服务器作为主节点,几个从节点各自训练一部分数据,将梯度传回参数服务器,计算后得到更新的模型参数。
另一个想法是模型并行化。

我们可以把模型转给不同的服务器或不同的线程。比如上图一张图片,对其进行卷积操作需要六层循环。我们可以把图像切割成 2 × 2 2\times2 2×2的块,这样每个线程或处理器可以解决图像的四分之一块,美中不足是块与块衔接的地方需要额外注意一下。
第三个想法是超参数并行化,可以在不同机器上调整学习率和权值衰减等。
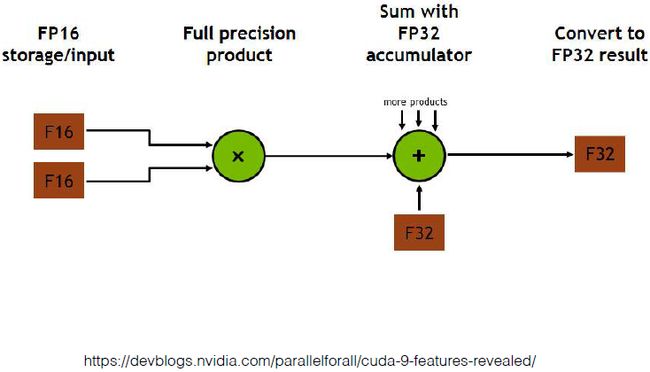
Mixed Precision with FP16 and FP32(16位浮点数和32位浮点数的混合精度)
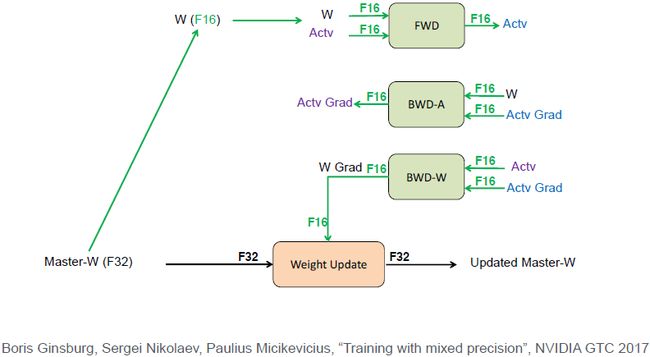
如上图所示。我们有一个32位的重要权重需要存储,先将其转换为16位浮点数,然后向前传递,经过16位权值16位的激活,得到一个16位的激活值。然后BP也是在用16位计算。这列我们得到一个16位的梯度,但在更新权值的时候W加上学习率乘以梯度必须要用32位计算。
Model Distillation
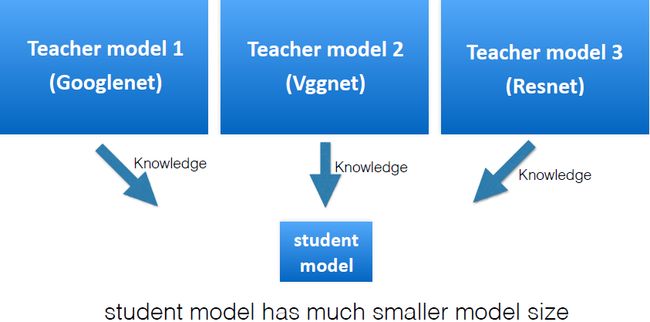
我们可以充分利用不同模型的优势吗?除了集成学习外,我们能不能把它们当做老师去教那些小的初级的NN,使它们表现出高级NN的性能?
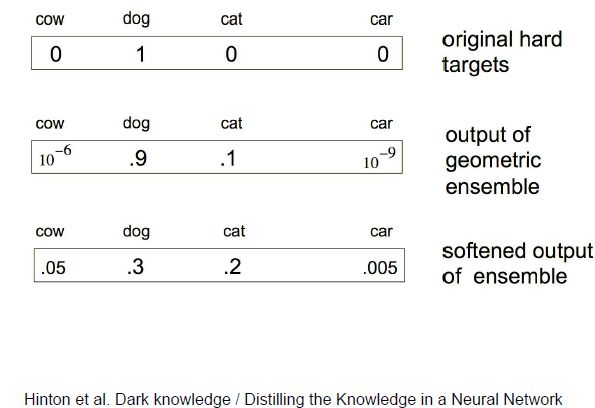
想做到这一点,我们不能使用车、狗、猫这种硬标签。这里需要一个软标签,如狗的概率是30%,猫的概率是20%。

数学上来表达,我们可以通过在softmax中控制参数T来控制它的柔和度。
DSD: Dense-Sparse-Dense Training
该方法是一种更好的正则化方法。
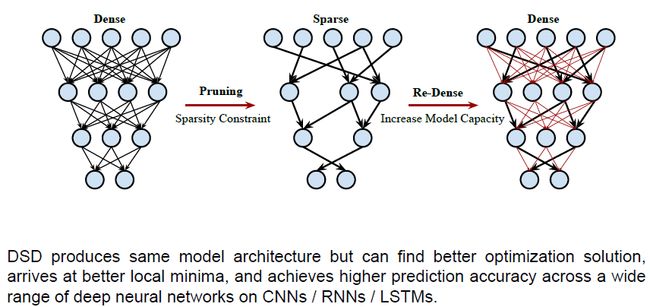
我们对原始神经网络剪枝后仍然保持预测精度,我们现在复原和重新训练标红的这些权重,确保每个权重一起训练,使得在低维空间训练后的模型更强大。
Hardware for Efficient Training
本博客与https://xuyunkun.com同步更新