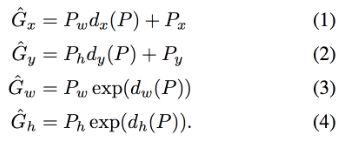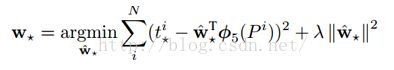Region Based CNN 系列之——(1) R-CNN思路及其基础整理

    现在对于从RCNN到FRCNN的论文已经有了很多优秀的博客来介绍，因此在这里，我只简单写一些思路性的东西，以及为了理解所加入的一些基础知识。

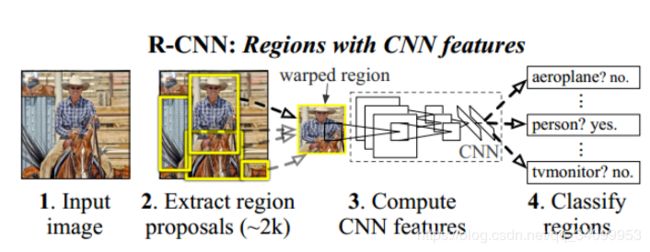
一、RCNN的整体结构

    

    如上图所示，RCNN的整体结构其实相对比较简单，首先为输入图像（可以是任意尺寸），其次通过Region Proposal 获取到约2000个候选区域，然后将这2000个候选区域直接resize成固定大小（227x227），再通过一个神经网络（CNN）来提取出固定维度的特征（4096维），最后用线性分类器SVM对其进行分类。

二、 Region Proposal（区域推荐）

    区域推荐的算法有很多，比如: objectness（物体性），selective search（选择性搜索），category-independent object proposals(类别无关物体推荐)，constrained parametric min-cuts（受限参最小剪切, CPMC)，multi-scal combinatorial grouping(多尺度联合分组)，以及Ciresan等人的方法，将CNN用在规律空间块裁剪上以检测有丝分裂细胞，也算是一种特殊的区域推荐类型。由于R-CNN对特定区域算法是不关心的，所以作者在文中用的是选择性搜索以方便和前面的工作进行可控的比较. 关于selective search（选择性搜索）的内容，如果想了解的话，可移步至：https://www.cnblogs.com/zyly/p/9259392.html

    文中作者是用selective search方法，选择出2000个候选框。

三、 特征提取与SVM分类

    首先将候选区域周边添加16的padding，然后各向异性resize成（224x224），经过5层conv和2层fc，变成4096-D的特征向量输出。将4096-D特征向量输入SVM分类器，进行分类。

四、测试阶段其他基础

    1、NMS（Non-Maximum Suppresiion1）:非极大抑制

        非极大抑制，也就是说抑制哪些不是最大值的元素。在分类任务，或者说目标识别领域，比如用滑动窗去检测，或者是用区域推荐算法选取出2000个候选框，都会面临一个问题：框与框之间是有重叠的。NMS的作用就是：选取那些邻域里分裂得分最高的，并且抑制那些得分低的窗口（或者候选区域）。

    如上图所示，由区域推荐算法所选择出来的候选区域，在每一个目标上，往往有多个框（多个候选区域），但是我们对于每个目标最终只选择一个区域，那么就要用到非极大抑制。

    非极大抑制（NMS）举例介绍：

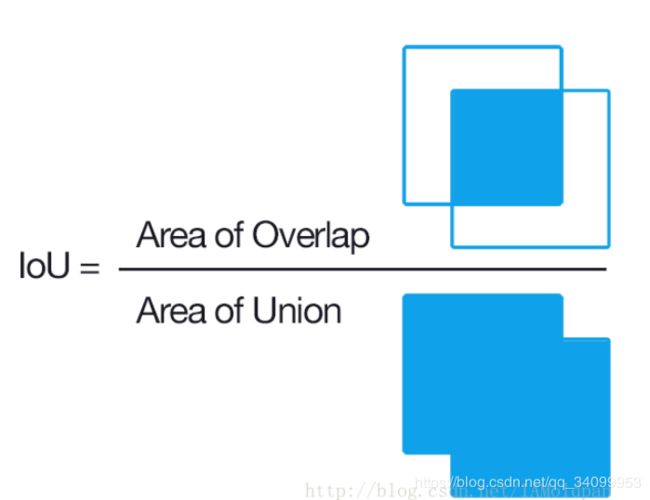
    比如上图中的人，区域推荐算法得到了三个框A,B,C，这三个框对于person这个分类的得分分别是0.88,0.92,0.99，那么对三个框用其得分从大到小排序为C、B、A。 分别计算C,B相对于A的IoU，根据所设定的阈值（比如Threhole_IoU = 0.3）,那么就意味着，如果C与A之间的IoU大于0.3，就要把C去掉，小于0.3，就把C留下。图中因为B和C相对于A的IoU都大于0.3，因此最后只有一个框A。

2. 边框回归（Bounding Box Regression）

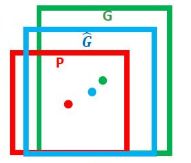
    由于区域推荐所得出的框一般情况下不一定和标注样本的框（Grond Truth）相等，因此在这里做了一个边框回归，来让预测出来的框更接近grond truth。

    如上图，红框P为区域推荐得到的框，（其中为框中心坐标，为框的宽和长），绿框G为Grond Truth， 篮筐为我们回归出来的结果。我们回归的过程，就是想通某种变换,来得到回归框。而想要将红框移动到篮筐或者绿框，其实我们只需要做一个平移和一个缩放就可以。

    平移量为为P_{w}的函数，缩放量为。（为什么学习的是而不是学习，以及为什么尺度缩放要用exp？后面会提到）。也就是说，我们要学习的量，就是（*代表）。那么我们需要比较的量是什么呢？根据公式（1）-（4），我们将Ground Truth的值代入：

    而所预测出来的，其实并不是用计算得到的，而是通过特征提取网络的Pool5feature（特征向量）与被学习的参数矩阵乘积的结果。即 .于是，损失函数就可以写成：

。而的求解可以表述为：

解释1：为什么用不直接用而是用。

    其实我们可以想一下，如果直接用框的坐标去回归框的坐标，那回归的过程就跟框里边的内容没有什么关系了，这样回归出来的函数，根本上来讲，是总结的proposol框与真实框之间的统计关系，与内容无关，那得到的结果肯定不好。

解释2：为什么回归偏移量的时候，要除以

    个人认为，因为卷积神经网络提取出来的特征，是与尺度无关的。而大框和小框的偏移量肯定不同，因此在回归偏移量的时候加上，实际是等价为偏移量的“尺度因子”，也就是说框越大，对应的偏移量有越大，框越小，偏移量越小。

解释3：为什么回归缩放尺度的时候，要用函数，而不是直接用

    其实理解起来就更简单了。我们来看预测时框宽度的表达式：，因为网络输出的是有正有负的，而框不可能是负值。而加上exp之后，就可以把缩放因子固定在正值，所以反推回去，学习的对比量就是。

解释4：为什么IoU越大越认为是线性变换

    其实主要还是看后两个，比如，变换一下：。我们知道在趋近于0的时候，可以近似，即越接近，那么变换越认为是线性。文中设定的IoU范围为0.6以上。

RCNN缺点：

(1)     训练分为多个阶段，步骤繁琐：微调网络+训练SVM+训练边框回归器；

(2)     训练耗时，占用磁盘空间大；5000张图像产生几百G的特征文件；

(3)     速度慢：使用GPU，VGG16模型处理一张图像需要47s；

(4)     测试速度慢：每个候选区域需要运行整个前向CNN计算；

(5)     SVM和回归是事后操作，在SVM和回归过程中CNN特征没有被学习更新