C语言 - 【回溯算法】迷宫问题 (顺序栈与链栈)

回溯算法可以看成是栈的一个十分成熟的应用，

本质上秉承着："正确前进错误返回" 的原则，通过入栈存储以前经过的所有节点，

当在一个方向上遇到死路，则依次弹栈返回前一个节点，继续按照相同的规律继续下一步的判断+入栈+弹栈操作。

 

< 本篇文章主要通过顺序栈与链栈(通过链表模拟)的方式实现迷宫问题 >

---

---

 

一：迷宫问题思路分析及实现（顺序栈）

1> 先不谈具体算法，首先我们需要实现迷宫的物理存储，

     可以采用二维数组来存储一个二维平面地图，使用0表示是通路，1表示是墙：

int maze[10][10] =        //迷宫在计算机中的物理存储方式
 {
    {1,1,1,1,1,1,1,1,1,1},
    {1,0,0,1,1,0,1,1,0,1},
    {1,0,0,1,0,0,0,1,0,1},
    {1,0,0,0,0,1,1,0,0,1},
    {1,0,1,1,1,0,0,1,1,1},
    {1,0,0,0,1,0,0,0,0,1},
    {1,0,1,0,0,0,1,0,0,1},
    {1,0,1,1,1,0,1,1,0,1},
    {1,0,0,1,1,0,0,1,0,1},
    {1,1,1,1,1,1,1,1,1,1}	
 };

2> 存储完地图之后，因为需要用到栈的操作，新建一个栈 (用于保存当前的位置坐标与下一个需要前进的方向)

  struct Try
  {
  	int i;
  	int j;
  	int d;
  }path[MaxSize]; 
  int top = -1;    //初始化栈指针 

3> 接下来写主体结构

   首先进行思路的整理：

* 函数参数传入的分别是起点坐标与出口坐标；

* 首先需要将起点入栈，然后开始循环，循环结束条件为栈空；

* 循环的第一步我们需要明白因为循环一次后栈中节点就会多一个，所以需要在开始判断栈顶节点的坐标是不是出口坐标；

   如果是出口坐标，则遍历整个栈输出坐标；

* 当判断当前栈顶的节点坐标不是出口坐标，顺时针进行下一步的寻找 (上右下左0123)，这样的方向定义可以任意，

   但是这里需要再考虑一点：

   当A ( 假设) 上方的路不通，判断右方的路是通的，然后右方经过一系列判断后是死路，返回A，

   此时就需要保证循环不会再从上方/右方开始执行，而且不会再原路向左返回 ( 返回操作只允许弹栈)，这就需要在新节点入栈

   之前存储这个节点的方向数据d，当弹栈后读取该节点，直接可以向下一个方向遍历，为了防止原路返回就要对已走的路

   进行标记 ( 数据替换)；

* 对原路的标记不仅可以看到运动轨迹 (次要) ，主要是为了防止节点方向参数d取3 (想像节点向右走) 的时候原路返回；

* 路不通直接弹栈，将被-1覆盖的迷宫数据再用0恢复，栈指针减1。

   下面给出该部分的代码实现：

void FindPath(int xb,int yb,int xe,int ye) 
{
	//起点入栈
	top++;
	path[top].i = xb;
	path[top].j = yb;
	path[top].d = -1;
	maze[xb][yb] = -1;    //标记起点     
	int i,j,k,d,find;    //映射变量与旗帜变量 
	while(top>-1)
	{
		i = path[top].i;
		j = path[top].j;
		d = path[top].d;
		if(i == xe && j == ye)
		{
			cout << "迷宫路径如下：" << endl;
			for(k = 0;k<=top;k++)
			{
				cout << "(" << path[k].i << "," << path[k].j << ") ";    //遍历整个栈，从栈底开始输出 
				if((k+1)%5==0) cout << endl;    //每行输出五个数据 
			} 
			cout << endl;
			return ; 
		}
		find = 0;
		while(d<4 && find == 0)    //循环判断上下左右每一个方向的情况，不是1直接入栈，是1再次循环，循环四次都是1则弹栈 
		{
			d++;
			switch(d)
			{
				case 0:
					i = path[top].i-1;
					j = path[top].j;
					break;
				case 1:
					i = path[top].i;
					j = path[top].j+1;
					break;
				case 2:
					i = path[top].i+1;
					j = path[top].j;
					break;
				case 3:
					i = path[top].i; 
					j = path[top].j-1;
					break;
			}
			if(maze[i][j]==0) find = 1;
		} 
		if(find == 1)
		{
			path[top].d = d;    //保存方向
			top ++;
			path[top].i = i;
			path[top].j = j;
			path[top].d = -1;
			maze[i][j] = -1;    //标记每一个通路为-1，防止返回，如果弹栈则将相应的-1换为0 
		} 
		else
		{
			maze[path[top].i][path[top].j] = 0;
			top--;
		} 
	} 
	cout << "无路可走！" << endl; 
}

4> 可以尝试打印出地图，查看更改后的地图

 

二：源代码（顺序栈）

 #include 
 #define MaxSize 100
 using namespace std;
 
 //首先使用二位数据建立迷宫矩阵:0表示通路，1表示墙 
 int maze[10][10] =        //迷宫在计算机中的物理存储方式
 {
    {1,1,1,1,1,1,1,1,1,1},
    {1,0,0,1,1,0,1,1,0,1},
    {1,0,0,1,0,0,0,1,0,1},
    {1,0,0,0,0,1,1,0,0,1},
    {1,0,1,1,1,0,0,1,1,1},
    {1,0,0,0,1,0,0,0,0,1},
    {1,0,1,0,0,0,1,0,0,1},
    {1,0,1,1,1,0,1,1,0,1},
    {1,0,0,1,1,0,0,1,0,1},
    {1,1,1,1,1,1,1,1,1,1}	
 };
 
 //建立顺序栈,用于存储当前的位置信息和下一步的方向 
  struct Try
  {
  	int i;
  	int j;
  	int d;
  }path[MaxSize]; 
  int top = -1;    //初始化栈指针 
 
void FindPath(int xb,int yb,int xe,int ye) 
{
	//起点入栈
	top++;
	path[top].i = xb;
	path[top].j = yb;
	path[top].d = -1;
	maze[xb][yb] = -1;    //标记起点     
	int i,j,k,d,find;    //映射变量与旗帜变量 
	while(top>-1)
	{
		i = path[top].i;
		j = path[top].j;
		d = path[top].d;
		if(i == xe && j == ye)
		{
			cout << "迷宫路径如下：" << endl;
			for(k = 0;k<=top;k++)
			{
				cout << "(" << path[k].i << "," << path[k].j << ") ";    //遍历整个栈，从栈底开始输出 
				if((k+1)%5==0) cout << endl;    //每行输出五个数据 
			} 
			cout << endl;
			return ; 
		}
		find = 0;
		while(d<4 && find == 0)    //循环判断上下左右每一个方向的情况，不是1直接入栈，是1再次循环，循环四次都是1则弹栈 
		{
			d++;
			switch(d)
			{
				case 0:
					i = path[top].i-1;
					j = path[top].j;
					break;
				case 1:
					i = path[top].i;
					j = path[top].j+1;
					break;
				case 2:
					i = path[top].i+1;
					j = path[top].j;
					break;
				case 3:
					i = path[top].i; 
					j = path[top].j-1;
					break;
			}
			if(maze[i][j]==0) find = 1;
		} 
		if(find == 1)
		{
			path[top].d = d;
			top ++;
			path[top].i = i;
			path[top].j = j;
			path[top].d = -1;
			maze[i][j] = -1;    //标记每一个通路为-1，防止原路返回，如果弹栈则将相应的-1换为0 
		} 
		else
		{
			maze[path[top].i][path[top].j] = 0;
			top--;
		} 
	} 
	cout << "无路可走！" << endl; 
}

void PrintMaze()
{
	cout << "包含有路径的迷宫：" << endl;
	for(int i = 0 ;i<10; i++)
	{
		for(int j = 0;j<10;j++)
		{
			printf("%3d",maze[i][j]);
		}
		cout << endl;
	}
}
 
 int main()
 {
 	FindPath(1,1,8,8);
 	PrintMaze();
 	return 0;
 } 

 

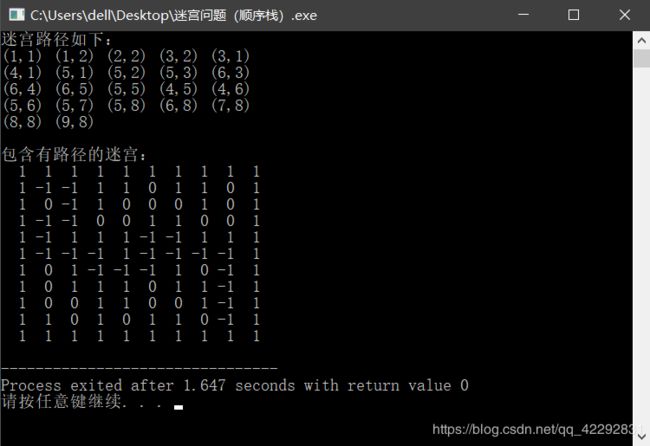
运行测试：

 

 

 

<2018.12.23更新>

三：链栈实现迷宫问题(通过链表模拟栈的输入与输出)

  源码（原理与顺序表实现一致）：

 #include 
 #include  
 #include 
 #define MaxSize 100
 using namespace std;
 
//建立链栈
typedef struct node
{
	int i,j,d;
	int Judge_Finish;
	struct node * link;
}LinkStack;
 

LinkStack * InitLinkStack()
{
	LinkStack * h;
	if(!(h=(LinkStack*)malloc(sizeof(LinkStack))))
	{
		cout << "Memory alllocate error!" << endl;
		exit(0);
	}
	h->Judge_Finish = 666;
	h->link = NULL;
	return h;
}
 
 //首先让起点入栈 
LinkStack * PushStack(LinkStack *h,int xb,int yb,int d)    //起点入栈,d表示方向 
{

	LinkStack *p,*s;
	p = h;

	if(!(s=(LinkStack*)malloc(sizeof(LinkStack))))
	{
		cout << "Memory alllocate error!" << endl;
		exit(0);
	}
	s->i = xb;
	s->j = yb;
	s->d = d;   //方向变量首先置-1 
	s->Judge_Finish = 0;
	s->link = p->link;
	p->link = s;
	return p;
}

LinkStack * PopStack_one(LinkStack *h)
{
	int temp_number[3] = {0};
	if(h->link == NULL)
	{
		cout << "LinkStack is Blank!" << endl;
		system("pause");
		cout << "Error:1" << endl;
	}
	LinkStack *p,*temp;
	p = h; 
	if(!(temp=(LinkStack*)malloc(sizeof(LinkStack))))
	{
		cout << "Memory alllocate error!" << endl;
		exit(0);
	}
	temp = p->link;	
	p->link = p->link->link;
	free(temp);    //这个时候，h/p指针指空，即h/p->link = NULL; 
	return h;
}

int* PopStack_two(LinkStack *h)    //仅仅返回栈顶数据，栈中的数据没有被实际弹出 
{
	static int temp_number[3] = {0};
	if(h->link == NULL)
	{
		cout << "LinkStack is Blank!" << endl;
		system("pause");
		cout << "Error:1" << endl;
	}
	LinkStack *p;
	p = h;
	temp_number[0] = p->link->i;
	temp_number[1] = p->link->j;
	temp_number[2] = p->link->d;
//	cout << "d=" << p->link->i<< "," << p->link->j << "," << p->link->d << endl<< endl; 
	return temp_number;
}

void TraverseStack(LinkStack *h)
{
	LinkStack *p;
	p = h;
	int count =0; 
	while(p->link)
	{
		cout << "(" << p->link->i << "," << p->link->j << ") ";
		p = p->link;
		if((count+1)%5==0)
		{
			cout << endl;
		}
		count++;
	}
}
 
 //首先使用二位数据建立迷宫矩阵:0表示通路，1表示墙 
 int maze[11][10] =        //迷宫在计算机中的物理存储方式
 {
    {1,1,1,1,1,1,1,1,1,1},
    {1,0,0,1,1,0,1,1,0,1},
    {1,0,0,1,0,0,0,1,0,1},
    {1,0,0,0,0,1,1,0,0,1},
    {1,0,1,1,1,0,0,1,1,1},
    {1,0,0,0,1,0,0,0,0,1},
    {1,0,1,0,0,0,1,0,0,1},
    {1,0,1,1,1,0,1,1,0,1},
    {1,0,0,1,1,0,0,1,0,1},
    {1,1,0,1,0,1,1,0,0,1},
	{1,1,1,1,1,1,1,1,1,1}		
 };
 

void FindPath(LinkStack *h,int xb,int yb,int xe,int ye) 
{
	//起点入栈
	PushStack(h,xb,yb,-1);
	maze[xb][yb] = -1;    //标记起点     
	int i,j,k,d,find;    //映射变量与旗帜变量 
	while(!h->link->Judge_Finish)    //当数据为666的时候终止,只是头结点赋值为666，其余入栈自动赋值为0 
	{

		int *number_1 = PopStack_two(h);    //仅仅弹出数据供显示，实际上并没有弹出数据 
		i = number_1[0];
		j = number_1[1];
		d = number_1[2];
		//cout << "d=" << i<< "," << j << "," << d << endl<< endl; 
		if(i == xe && j == ye)
		{
			cout << "迷宫路径如下(反向输出)：" << endl;
			TraverseStack(h);    //遍历输出 
			cout << endl;
			return ; 
		}
		find = 0;

		while(d<4 && find == 0)    //循环判断上下左右每一个方向的情况，不是1直接入栈，是1再次循环，循环四次都是1则弹栈 
		{
			d++;
			int *number_2 = PopStack_two(h);    //获取栈顶数据信息 
			switch(d)
			{
				case 0:
					i = number_2[0]-1;
					j = number_2[1];
					break;
				case 1:
					i = number_2[0];
					j = number_2[1]+1;
					break;
				case 2:
					i = number_2[0]+1;
					j = number_2[1];
					break;
				case 3:
					i = number_2[0]; 
					j = number_2[1]-1;
					break;
			}
			if(maze[i][j]==0) find = 1;
		} 
		if(find == 1)
		{
			h->link->d = d;    //在新一个数据入栈之前存储前一个数据的方向变量
			//cout << "入栈信息："; 
			//cout << h->link->i << ":" << h->link->j;
			//cout << "h->link->d : " << h->link->d << endl << endl; 
			h = PushStack(h,i,j,-1);

			maze[i][j] = -1;    //标记每一个通路为-1，防止原路返回，如果弹栈则将相应的-1换为0 
			//cout << "走过的路径换为-1的坐标：" << i << "-" << j << endl; 
		} 
		else
		{
			int *number_3 = PopStack_two(h);    //获取栈顶数据信息 
			maze[number_3[0]][number_3[1]] = 0;
			//cout << "(" << number_3[0] << "," << number_3[1] << ")----------归0" << endl;
			h = PopStack_one(h);
			//cout << "弹栈后的下一个路径点：" << "(" << h->link->i << "," << h->link->j << ") --- 方向变量d：" << h->link->d << " --- Judge_Finish：" << h->link->Judge_Finish << endl;
		} 
	} 
	cout << "无路可走！" << endl; 
}
 
void PrintMaze()
{
	cout << "\n包含有路径的迷宫：" << endl;
	for(int i = 0 ;i<11; i++)
	{
		for(int j = 0;j<10;j++)
		{
			printf("%3d",maze[i][j]);
		}
		cout << endl;
	}
}
 
 int main()
 {
 	LinkStack *h;
 	h = InitLinkStack();
 	FindPath(h,1,1,9,8);
 	PrintMaze();
 	return 0;
 } 

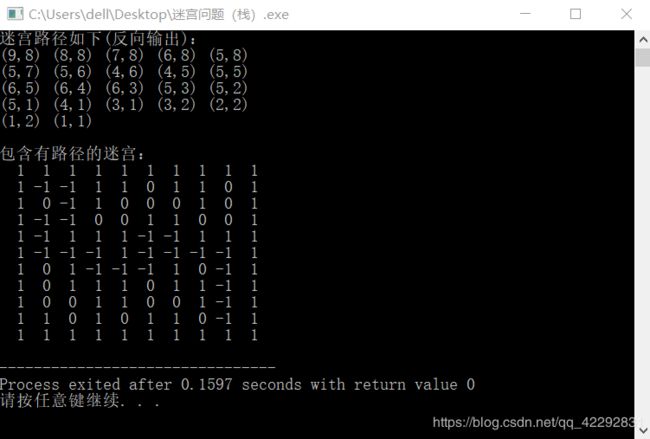
运行测试（源码中注释掉的语句是在调试中起到测试作用）：

 

 

 

 

 

---

---

                            最快的脚步不是跨越，而是继续，最慢的步伐不是小步，而是徘徊。

---

---