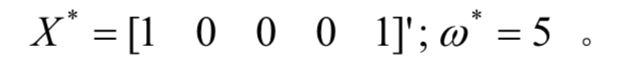数学建模(一):全面探索线性规划
&1.线性规划问题定义:
在一组⎡线性⎦约束条件限制下,求一⎡线性⎦目标函数的最大值和最小值。
线性规划问题的主要难点在于模型的建立,若想快速准确地建立模型,合理选取决策变量是关键。
&2.线性规划的matlab形式
Matlab规定的线性规划标准形式为
可以通过在目标函数或约束不等式前添加负号来将非标准线性规划转化为标准线性规划形式。
求解程序为[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
这里 fval 返回目标函数的值,LB 和 UB 分别是变量 x 的下界和上界,x0 是 x 的初始值,OPTIONS是控制参数。
举一个例子:
求解matlab程序c=[2;3;1];a=[1,4,2;3,2,0];b=[8;6]; [x,y]=linprog(c,-a,-b,[],[],zeros(3,1))
&3.可以转化为线性规划的问题

注意到:对于任意的xi,存在ui,vi>=0满足xi=ui+vi,|xi|=ui-vI;
这样就可以用xi与|xi|来表示ui与vi。记u=[u1…un]T,v=[v1…vn]T;从而上述问题被转化为: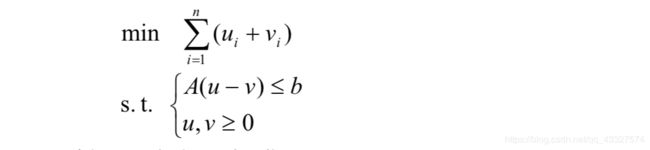
此时便可以轻松求解。
&4.产销平衡问题

这里我们的假设是所有产地商品的总出产量与所有销地的总需求量是相等的,我们将决策变量xij定义为从第i个产地运到j销地的商品数量,于是可以得到目标函数为
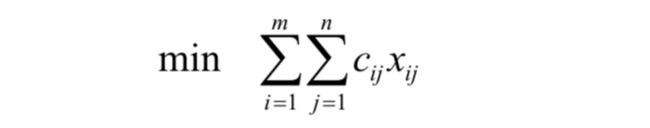
而约束条件就能够轻松得出了:对于xij有非负性约束;对于第i个产地,要求它到所有销地的商品量和为ai;对于第j个销地,要求所有产地到它的商品量和为bj;
综上所述,我们可以得到约束条件为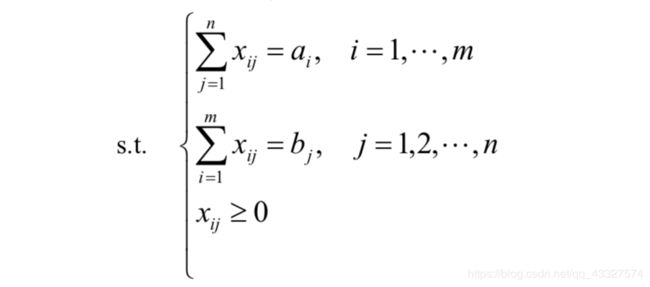
由此发现,这是一个线性规划问题,我们可以轻松地使用matlab求解。
&5.指派问题
1)指派问题的定义

我们令C=(cij),称C为指派问题的系数矩阵;引入决策变量xij,当分配第i人去完成第j项工作时,xij=1,否则xij=0。于是该问题的目标函数为
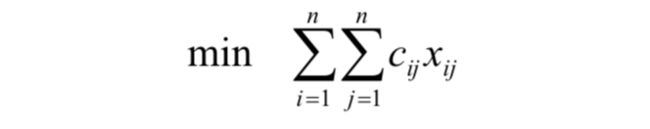
而我们由题意得到,每个人只能完成一项工作,而每一项工作也只能由一个人完成,同时决策变量被限定了取值,于是我们可以得到约束条件为
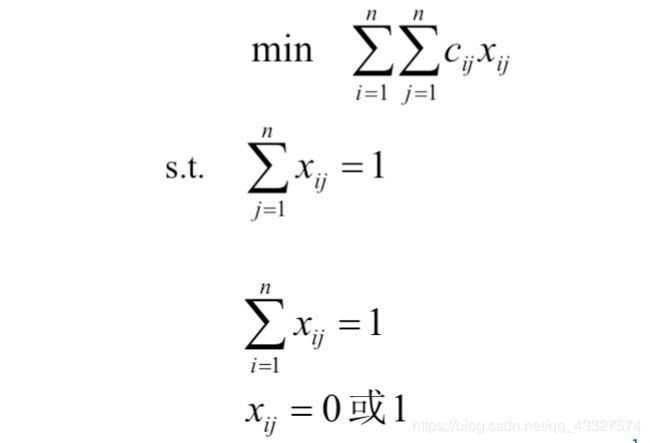
我们令X=(xij),代表着指派问题的可行解,那么易知X矩阵的每一行每一列都是只能有一个1的,其他都是0;变量xij只能取0或1,因此这也是一个0-1规划问题,但指派问题与一般的0-1规划问题不同,它的求解难度并不是很大。
(2020.4.14 后续待更新)
2)求解指派问题的匈牙利算法
由匈牙利数学家Konig提出的指派问题求解方法,基于以下事实:如果系数矩阵C=(cij)一行(或列)中所有元素减去一个相同的实数,得到一个新的系数矩阵B=(bij),分别以这两个矩阵作为系数矩阵的指派问题具有相同的最优解。

这里cij指的是将第i人指派去完成第j个任务所需要花费的时间,我们有两个最基本的思考角度:要么是把每个任务指派给能最短时间内完成它的人,要么是让每个人去完成他最短时间完成的任务;(在不考虑指派的任务或人重复的情况下);那么我们可以把每一行元素减去该行的最小值,则第i行的0代表的是第i人最短时间完成的任务,可以得到:

我们可以发现第三个人与第四个人最短时间完成的都是第四个任务,而第三个任务没有人可以指派,于是我们将第三列减去这一列的最小值,得到
于是便可以得到最优解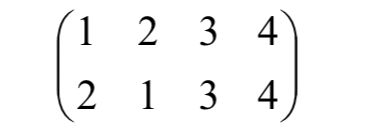
这是一个较为简单的例子,我们接下来看一个稍微复杂一点的指派问题
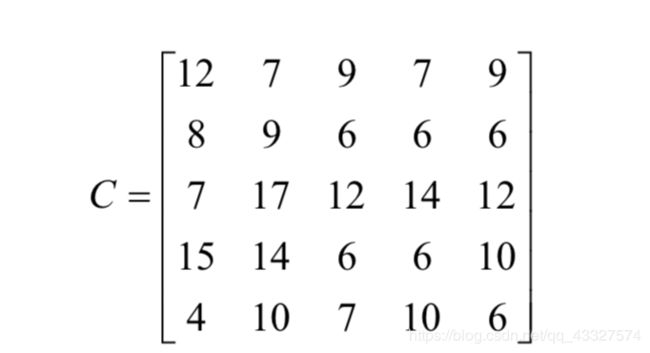
我们让每行减去该行的最小值,可以得到等价系数矩阵
此时使用之前的方法,会发现代表未指派的第五个任务的第五列是含0,但指派的人已经有了任务,于是我们进行下述操作:
1)将代表未分配任务的第i人那一行打勾;
2)对打勾的行中含有的0元素所在那一列打勾;
3)对打勾列中已经被分配的0元素所在的那一行再进行打勾;
重复2)3)操作,直到无法再继续打勾为止;

我们使用直线划去没有打勾的行和打勾的列,能够用最少的直线将矩阵中所有的0元素覆盖,找出打勾行中元素的非零最小值,令打勾的行减去这个值,打勾的列加上这个值,可以重复这个过程,直到得到新的有解的系数矩阵为止。新得到的系数矩阵与原系数矩阵代表的指派问题同解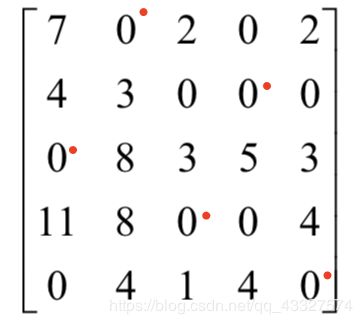
可以得到最优指派为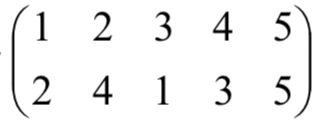
&6.对偶理论
1)原始问题和对偶问题
对于一个原始线性规划模型
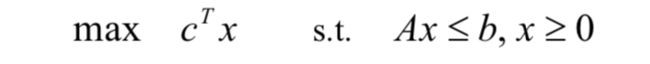
我们可以得到他的对偶问题
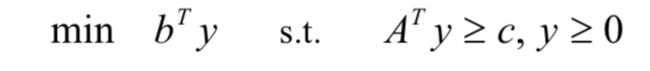
2)对偶问题的一些基本性质
1.对称性:对偶问题的对偶是原问题;
2.无界性:若原问题是无界解,则其对偶问题也是无界解;
3.最优解性质:对于两问题的可行解来说,当两问题的目标函数代入可行解后得到的值相等时,这时的可行解是最优解;
4.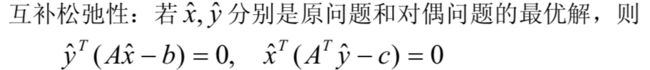
从互补松弛式可以看出,假若原问题(对偶问题)的最优解不满足约束问题中的等号时,则对偶问题(原问题)对应的最优解的变量的值一定为0;

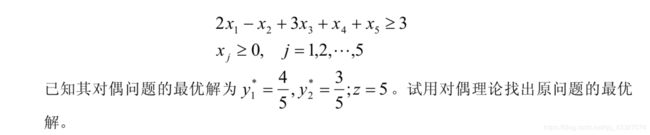
写出它的对偶问题,可以得到
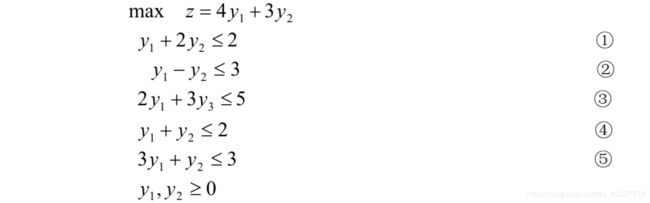
将题目中给出的解,代入五个不等式中,发现只有第一个和第五个不等式满足等号,那么根据互补性松弛,我们可以得到x2,x3,x4都为0,原始问题的限制条件等号成立,所以有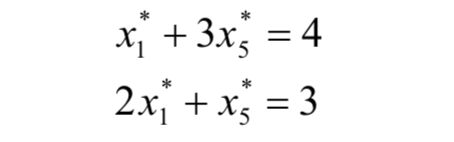
可以解得