【回归预测】SVM基础实战篇之经典预测（三）

​ 【玩点有趣的】这几篇SVM介绍是从0到1慢慢学会支持向量机，将是满满的干货，都是我亲自写的，可以随我一起从头了解SVM，并在短期内能使用SVM做到想要的分类或者预测~我也将附上自己基础训练的完整代码，可以直接跑，建议同我一样初学者们，自己从头到尾打一遍，找找手感，代码不能光看看，实践出真知！

​ 回顾一下，上上篇，我们建立和比较了线性分类器和非线性分类器，比较了多元线性核函数和线性核函数，解决了类型数量不平衡问题，上篇，我们使用SVC做了简单的分类，话不多说，今天我们开始SVR做回归预测，原理篇和实战基础一 请参见上几篇博客，我们循序渐进慢慢贴近真实情景！解决生活问题

---

估算交通流量

首先做一个比较有趣的应用，我们使用了SVR来预测：在洛杉矶棒球队进行主场比赛期间，体育场周边马路通过的汽车数量

如图：

这里一万七千条记录数据，分别表示：星期，时间，对手球队名，比赛是否正在进行，通过汽车的数量

【完整代码】上代码：

import numpy as np
from sklearn import preprocessing
from sklearn.svm import SVR

input_file = 'traffic_data.txt'

X = []
count = 0
with open(input_file, 'r') as f:
    for line in f.readlines():
        data = line[:-1].split(',')
        X.append(data)

X = np.array(X)

label_encoder = []
X_encoded = np.empty(X.shape)
for i, item in enumerate(X[0]):
    if item.isdigit():
        X_encoded[:, i] = X[:, i]
    else:
        label_encoder.append(preprocessing.LabelEncoder())
        X_encoded[:, i] = label_encoder[-1].fit_transform(X[:, i])

X = X_encoded[:, :-1].astype(int)
y = X_encoded[:, -1].astype(int)

params = {'kernel': 'rbf', 'C': 10.0, 'epsilon': 0.2}
regressor = SVR(**params)
regressor.fit(X, y)

import sklearn.metrics as sm

y_pred = regressor.predict(X)
print("Mean absolute error =", round(sm.mean_absolute_error(y, y_pred), 2))
print('mean squared error=',round(sm.mean_squared_error(y, y_pred),2))
print('median absolute error=',round(sm.median_absolute_error(y, y_pred),2))
print('explained variance score=',round(sm.explained_variance_score(y, y_pred),2))
print('R2 score=',round(sm.r2_score(y, y_pred),2))
input_data = ['Tuesday', '13:35', 'San Francisco', 'yes']
input_data_encoded = [-1] * len(input_data)
count = 0
for i, item in enumerate(input_data):
    if item.isdigit():
        input_data_encoded[i] = int(input_data[i])
    else:
        input_data_encoded[i] = int(label_encoder[count].transform([input_data[i]]))
        count = count + 1 

input_data_encoded = np.array(input_data_encoded)

print("Predicted traffic:", int(regressor.predict([input_data_encoded])[0]))

解说一下：

X = []
count = 0
with open(input_file, 'r') as f:
    for line in f.readlines():
        data = line[:-1].split(',')
        X.append(data)

X = np.array(X)

​ 使用文件操作逐行读取并使用spilt通过逗号分割得出最后一列的数据（汽车通行量）append进到数组X中，构成我们的初始数据， 再通过sklearn.preprocessing.LabelEncoder()进行标准化标签，将标签值统一转换成range(标签值个数-1)范围内 ，最后使用fit_transform(X[:, i])进行fit和transform转换成计算机可读的数字（矩阵）形式：
【数据预处理】代码如下

label_encoder = []
X_encoded = np.empty(X.shape)
for i, item in enumerate(X[0]):
    if item.isdigit():
        X_encoded[:, i] = X[:, i]
    else:
        label_encoder.append(preprocessing.LabelEncoder())
        X_encoded[:, i] = label_encoder[-1].fit_transform(X[:, i])
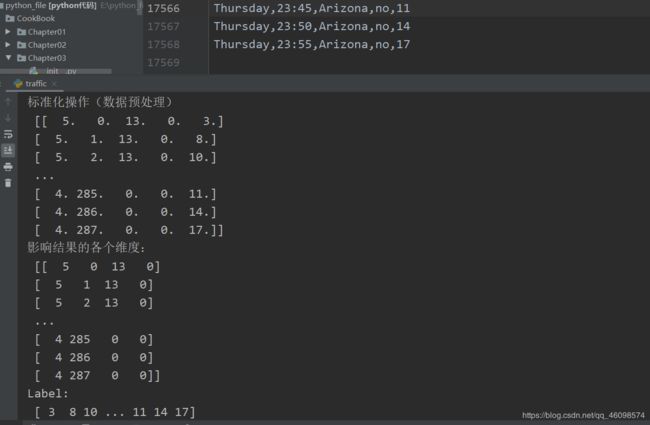
print('标准化操作（数据预处理）\n', X_encoded)
X = X_encoded[:, :-1].astype(int)
y = X_encoded[:, -1].astype(int)
print('影响结果的各个维度：\n', X)
print('Label:\n', y)

看看结果：

可以看出：每行每列，带有英文的字符也被清洗成了数字，这其中是有逻辑含义的，可以用过查看源码明白。同样的也可以通过Pandas实现上述操作。然后我们使用切片操作分割出label和X

后续就是使用SVR构建预测器，然后“喂它数据”：

params = {'kernel': 'rbf', 'C': 10.0, 'epsilon': 0.2}
regressor = SVR(**params)
regressor.fit(X, y)

import sklearn.metrics as sm

y_pred = regressor.predict(X)
print("Mean absolute error =", round(sm.mean_absolute_error(y, y_pred), 2))
print('mean squared error=',round(sm.mean_squared_error(y, y_pred),2))
print('median absolute error=',round(sm.median_absolute_error(y, y_pred),2))
print('explained variance score=',round(sm.explained_variance_score(y, y_pred),2))
print('R2 score=',round(sm.r2_score(y, y_pred),2))
input_data = ['Tuesday', '13:35', 'San Francisco', 'yes']
input_data_encoded = [-1] * len(input_data)
count = 0
for i, item in enumerate(input_data):
    if item.isdigit():
        input_data_encoded[i] = int(input_data[i])
    else:
        input_data_encoded[i] = int(label_encoder[count].transform([input_data[i]]))
        count = count + 1 

input_data_encoded = np.array(input_data_encoded)

print("Predicted traffic:", int(regressor.predict([input_data_encoded])[0]))

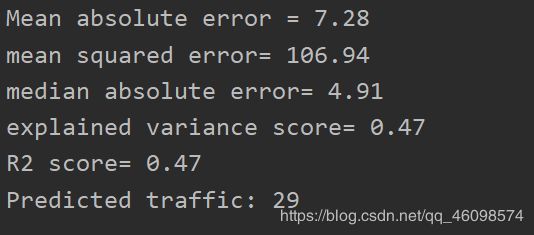
最后我们直接看结果

这是这个情况下的预测汽车数量，[‘Tuesday’, ‘13:35’, ‘San Francisco’, ‘yes’] Predicted traffic =29

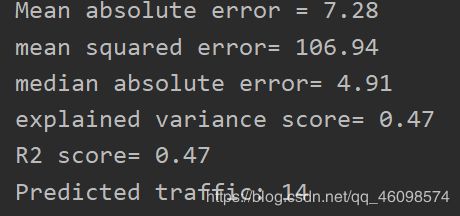
[‘Thursday’, ‘23:10’, ‘Arizona’, ‘no’]下： Predicted traffic =14

我们来看一下这几个判别情况：
Mean absolute error =7.28

mean squared error= 106.94
median absolute error= 4.91
explained variance score= 0.47
R2 score= 0.47

介绍一下：

建立回归器后，需要建立评价回归器拟合效果的指标模型。

平均误差(mean absolute error):这是给定数据集的所有数据点的绝对误差平均值

均方误差(mean squared error):给定数据集的所有数据点的误差的平方的平均值，最流行

中位数绝对误差(mean absolute error)：给定数据集的所有数据点的误差的中位数，可以消除异常值的干扰

解释方差分(explained variance score)：用于衡量我们的模型对数据集波动的解释能力，如果得分为1.0，表明我们的模型是完美的。

R方得分(R2 score)：读作R方，指确定性相关系数，用于衡量模型对未知样本预测的效果，最好的得分为1.0，值也可以是负数。

通常情况下，尽量保证均方误差最低，而且解释方差分最高。

可以看到，我们使用的这个SVR回归器不是那么完美，甚至误差有一些。

昨天也跟朋友有提高过：
机器学习算法和平常的数据结构与算法的区别：通俗的说，前者注重accuracy，recall，precision，F1_score,后者注重时间复杂度和空间复杂度，

那么我们的SVR回归器的这个误差当然是难以容忍的，我们来分析一下原因：

一：参数误差：没有通过网格搜索或者k折交叉验证，贝叶斯优化调整超参数，svr的参数误差很大，不同的参数，差别十万八千里。

二：原始数据标准化过程：transform问题，或者未归一化，

三：SVR容易欠拟合

这些都是待改进问题。

下面我们比较一下常用的回归与分类算法：

（资料来源百度，后期我们会把常用的算法介绍，并且实战（实战是理论的体现，两者结合才会绽放绚丽光芒））

一、朴素贝叶斯

• 优点：小规模表现好，适合分类任务，适合增量训练。
• 缺点：对输入形式敏感（数值型可以考虑二分？），很多时候要拉普拉斯平滑。

二、决策树

• 优点：计算简单，可解释型强，能处理缺失值，不相关特征，能多分类。可以设计为回归模型。
• 缺点：过拟合问题（预剪枝、后剪枝）。RF可以解决一些，因为对数据样本的bagging加上对特征的随机选择（比如选 n**0.5个特征）引入了随机，减小了过拟合。

三、logistic

• 优点：实现简单，速度快，存储小。
• 缺点：容易欠拟合，只能二分类（改进，1v1,1v多，多v多），对outlier比较敏感，不支持非线性划分。

四、线性拟合（LSM/Ridge/Lasso）

• 优点：实现简单，计算简单（close form，闭式解）。
• 缺点：不能拟合非线性数据。

五、kNN

• 优点：思路简单（近朱者赤），理论成熟，可分类可回归，可非线性，对outlier不敏感。
• 缺点：计算量大，样本不平衡，大内存开销。
• 注：其实是免训练的模型。也算优点吧。

六、SVM

• 优点：可用于线性/非线性(核：高斯核、多项式核、字符串核、RBF、Logistic核)，可以用于回归SVR，低泛化误差，易解释性，抗数据扰动（outlier），存储小（支持向量）。
• 缺点：需要手动选参数，选核函数，原始的SVM是二分类。

七、Adaboost

• 优点：低泛化误差，易实现，准确率高，参数少，多分类。降低偏差bias（预测与实际的差）。
• 缺点：对outlier敏感（因为会调误分类权重），不能并行。
• 注：和GBM（GBRT/GBDT）都是boosting，不同在于权重调整一个根据误分类数据，一个根据梯度。

八、Random Forest

• 优点：处理高维数据不用做特征选择；能给出特征重要比；oob，使用无偏估计，泛化能力强；树之间独立，可并行，因而训练快；不平衡数据可以平衡误差；一部分特征遗失仍然可以有精确度。不用剪枝。减低方差variance（数据扰动产生的不同结果）。
• 缺点：在某些噪音较大的分类或者回归问题上过拟合；对于不同取值的属性的数据，取值划分较多的属性会对RF产生更大的影响，导致权值不可信。

九、xgboost

• 基分类器除CART外还支持线性分类器，相当于LR、Ridge。
• GBDT用一阶，xgboost用一阶和二阶进行梯度优化。
• 代价函数里有L1和L2正则，控制复杂度减小过拟合。
• shrinkage可以设置学习速率。
• 借鉴了RF的列抽样（选一些特征），引入随机（深度学习的dropout也是引入了随机），降低过拟合，减少计算。
• 缺失值的样本也可以自动学习分裂方向。
• 支持并行，不是tree粒度的，而是特征粒度的。
• 可并行的近似直方图算法，高效生成候选的分割点。

十、k-means（属于EM思想）

• 优点：简单快速，团状效果好，O(nkt),通常局部收敛

• 缺点：需要指定k，初始值敏感，需要指定距离定义/中心定义，数据形状敏感(比如密度形状的用DBSCAN，比如流形学习)，对outlier敏感。

下一期我们先做一个真实项目实战，后续我们遇到SVM问题，再继续补充

​ 这是我们的SVM第四期文章了，已经大致明白了他的原理和基本用法，我们使用了sklearn对SVM的封装，也使用了numpy对SVM的复现，还可以使用libsvm和opencv对svm的封装。接下来我们结合计算机视觉做有趣的实验，先卖个关子（关注博主，下期继续），上图！

这是帮朋友做的毕业设计，其中有一些bug需要修复，一些问题，需要优化，并且，代码不是我写的，朋友给我的。我帮助他跑起来，并且现在开始帮助他修改，优化代码，学C++，推荐算法去了，关注博主，敬请期待！

上海第二工业大学智能科学与技术大二 周小夏（CV调包侠）