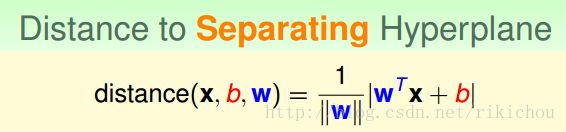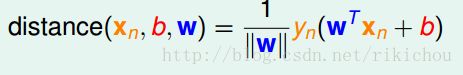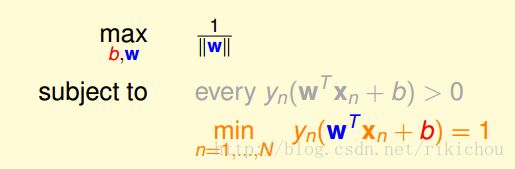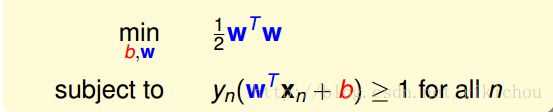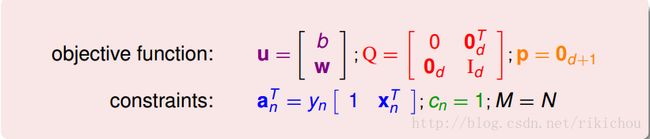林轩田--机器学习技法--SVM笔记1--线性支持向量机(linear+SVM)
支持向量机
以下是我学习林轩田–机器学习技法的SVM章节的学习笔记,以及《统计学习方法》第七章–支持向量机的内容,如有错误还请大家及时提出,谢谢
1. 什么是支持向量机
支持向量机(support vector machine,SVM)是一种二类分类模型,他的基本模型是定义在特征空间上的间隔最大的线性分类器。 间隔最大使它有别于感知机;支持向量机还包括核技巧,这使它成为实质上的线性分类器。支持向量机的学习策略就是间隔最大化,可形式化为一个求解凸二次规划(convex quadratic programming)的问题,也等价于正则化的合页损失函数的最小化问题,支持向量机的学习算法是求解凸二次规划的最优化算法。
–《统计学习方法》.李航
感觉挺懵的是吧?什么特征空间的最大间隔?什么是核技巧?这个凸二次规划又是什么鬼?跟正则化还有关系?这就是我刚看到上面那段文字时的疑问,不要着急,接着往下走。
2. 支持向量机的动机
因为支持向量机属于一种二分类的模型,所以现在从简单的线性分类器入手。
线性分类器说的是什么呢?
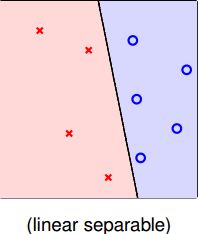
如上图,我有一堆线性可分的‘圈圈’和‘叉叉’的样本,我想要找到一个分割线(二维特征)或者平面(三维特征)或者超平面(高维特征)将这些圈圈和叉叉准确无误地分开。例如我们之前学习过的PLA/pocket算法。
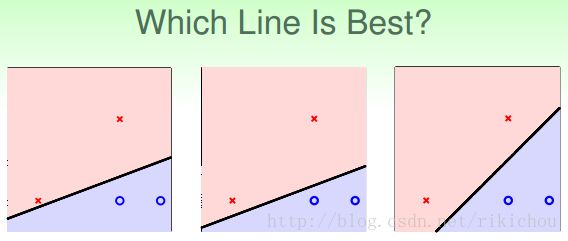
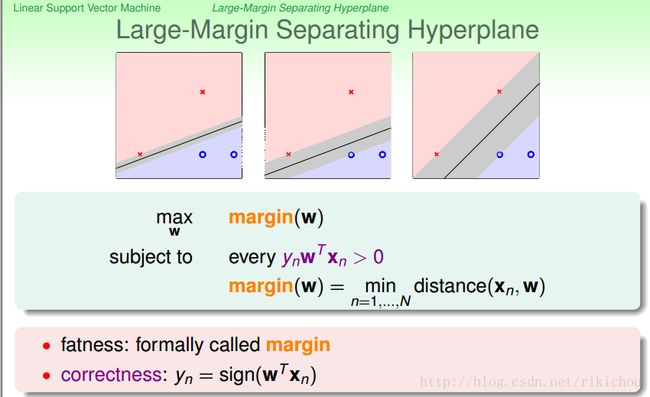
好,那现在如果我们有一堆线性可分的样本,那么我们有可能有无限多条分割线能够将其正确分开,那么请问,针对以下三种分法,您更倾向于哪一种分割线呢?或者说您认为哪种分割线更可靠呢?
我相信大家都选择了最右边的那一条线,现在我们就可以问问我们自己,我们选择最右边的那一条线的凭据是什么?如果大家不知道怎么表述的话,我这里倒是又一个比较简单的解释。
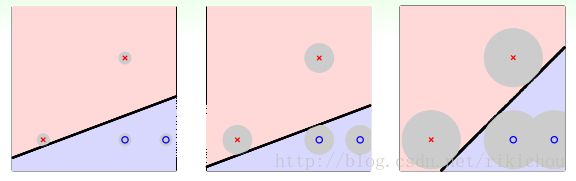
如上图中,想象上图中的三种模型都根据样本点拟合出了各自的分割线。那现在如果有一个新的样本,想要在以上三个拟合出来的模型中进行预测,如果新的样本点和用于训练的样本点很接近,但是由于测量误差或其他原因,总会使我们的测量点偏离样本点,上图中每个样本点的灰色部分表示该样本点可接受的误差范围(仅仅考虑离分割线最近的几个点),如果超过该范围,可能会导致错误得分类结果。从上图可以看出,当我们的分割线距离样本点越远时,对噪声的容忍度就越高,越不容易出现误分类的情况,分类也就越可靠!之前机器学习基石中我们知道,噪声是造成overfitting的主要原因之一,所以对噪声的容忍度越高也使我们更能减少overfitting。所以我们希望在正确分类所有样本的情况下,分割线离样本越远越好!这就是我们选第三个模型的原因。
所以现在我们的出发点就是在正确分类的情况下,分割线离每个点越远越好。
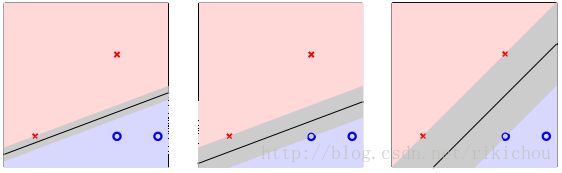
所以如果我们要看线和点隔多远的话,从另一个角度来讲,也可以说是线有多胖。如下图,一条线有多胖,表示当这条线往两边延伸,延伸多长会碰到最接近的点。最右边的线很胖,我们喜欢这种。最左边的线一下子就碰到了最近点了,我们认为它不够强壮。
所以,我们就是要找比较胖的线,胖—与最近的点的距离,最胖—与最近的点的距离最大。
上述就是支持向量机的动机,我们并不是像PLA那样随表找一条能正确划分所有样本的线,我们是要找一条能正确分类且最胖的线。
3. 最大间隔问题
通过上面的讲解,可以将我们的问题描述为:
其中,目标为找到一条最胖的分割线。
限制条件有两个:
* 这条线必须能够将所有样本划分正确
* 这条线是所有的分割线中,到最近样本点的距离最大的线
在之后的讨论中,我们将不再使用胖这个描述,使用更正规的描述–margin,也称为边界。
所有样本划分正确的意思是,WXn预测的正负号,要和Yn相同。所以上图可以进一步地表示为下图
所以我们现在明确了目标:找出largest-margin(边界最宽) separating(正确分类)的分割线或者超平面(以下统一叫做超平面)。
3.1 如何计算点到超平面的距离
我们的目标是找出一个边界最宽且正确分类的超平面,在这之前,首先要将上图中的文字描述转换为数学表达式。首先看看如果计算点到超平面的距离,也就是distance(Xn, w)。其实这个在几何或者线代上有公式可用,在这里不做推导,林老师有做相关的推导,有兴趣的同学可以看一下。所以我们可以轻易地得到
对于这个距离我们有一个正式的名称叫做:几何间隔
但是几何间隔的表达式中有绝对值的符号,这是不利于我们优化的。因为我们要求我们的超平面能够将所有样本都正确分类,所以Yn.(WXn + b)肯定为正数,进而可以将绝对值去掉。表示为下图所示。其中Yn.(WXn + b)有一个正式的名称叫做:函数间隔
3.2 模型表示
所以经过了上面的转换,我们的问题有了新的数学形式,表述如下:
好了,有了新的数学形式了,但是好像还是不会解,因为max之类的条件总是不利于求解最佳问题的。所以我们就要想办法把max去掉。
假设我们已经找到了这个最佳的超平面,这个超平面的方程式为WX + b = 0,如果现在我将W和b参数同时放大3倍,得到3WX + 3b = 0,从几何坐标上来看,无论我们将W和b同时放缩多大(0除外),我们的超平面的几何位置是不会改变的,也就是我们的几何间隔是不会改变的。所以我们可以对最佳超平面进行任意放缩,而不影响其最优的性质。
由于这个超平面是最佳超平面,假如我们此时的函数间隔为100,当我们对最佳超平面进行放缩的时候,函数间隔Yn.(WXn + b)是会按照比例进行放缩的。
所以回到我们的问题上,我们可不可以这样假设,我们最小的函数间隔刚好等于1。因为最佳超平面肯定会有一个最小函数间隔n,我们可以将超平面放缩n倍从而使最小的函数间隔为1,而不影响最佳超平面。所以这样的假设成立。
那这样做有什么好处呢?因为最小的函数间隔Yn.(WXn + b) = 1,所以,margin(w, b)就可以简单地写为1/||W||
所以新问题可以进一步地表示为
由于我们的新条件的限制性更强(要求每一个点的函数间隔都大于等于1),所以我们可以把灰色部分的条件去掉。得到以下表示
咦,好像还是不会解!之前不是说好了把max条件去掉吗?怎么又出来一个min条件。好,现在就来去掉这个条件。
那我们可不可以对现有的条件做一个放松呢?现有的条件是所有的样本点中,最小的函数间隔等于1,那我可不可以改为,所有的样本点的函数间隔都大于或者等于1呢?
这样的条件有利于我们的最优化的求解。但是,这样随意改变限制条件不会对最优解产生影响么?也就是说当我使用该条件得出最优解后,然后使用该最优解计算所有样本点的函数间隔,是否会产生所有的函数间隔均大于1的情况?下面就来证明一下我们的担心是多余的!
如果现在找到了最优解(w,b),且通过计算发现最小的函数间隔为1.126(随意的一个值,仅仅用于说明最小函数间隔不为1.使用反证法),因为是最优解,所以当前的(w,b)组合一定是使1/||w||的值最大的组合。那真的是吗?如果我们现在将(w,b)同时缩放1.126倍,那我们的最小函数间隔变为1,是在我们的限制范围内。如果说之前的(w,b)是最优解,那么现在缩放后的(w,b)一定会是1/||w||减小。但是事实却不是这样,当我们的w减小时,1/||w||的值在增加,说明最小函数间隔为1.126时的(w,b)的解并不是最优解。同理可证,在函数间隔非1时的(w,b)均不是最优解。所以说,当我们寻找到最优解时,每个样本点的函数间隔值一定是大于等于1的。
所以我们现在有了一个更友好的限制条件,接下来再在目标优化函数上做一点点改变就好。
- 相比于max的形式,我们更喜欢min形式。所以讲原来的最大化问题取倒数变为最小化问题
- 接着,由于计算W的长度的过程中又一个开根号,所以我们直接求W的平方
- 为了便于之后的计算,我们在函数前面加上一个1/2
所以我们就得到了最大间隔问题的标准形式
4.最大间隔问题求解
上一节,我们通过一系列的转换,将最大间隔问题的最终形式定格在如下:
现在的问题就是找到一个符合限制条件的目标函数的最佳解。想想我们以往的算法analytic solution?GD?SGD?因为该问题是有条件限制的缘故,以前的算法都无法使用。
但是,我们的问题有如下特点:
- 目标函数是一个凸的二次函数
- 所有的条件都是关于w,b的一次式。也就是说条件都是线性的
有这些特性的最优化问题我们都叫做二次规划问题。在数学上,该问题属于很容易优化的问题,网上有大量的工具可以用于求解该类问题。所以我们就可以将我们的问题表示为标准的二次规划的形式,然后再代入别人的工具来解决就好了。(其实我们之前对最大间隔问题所做的转换都是为了向二次规划上靠拢)
4.1 使用QPsolver解二次规划
我们的问题以及标准的二次规划问题如下图所示:
- 标准的二次规划问题优化的目标是u向量
- Q矩阵存储的是目标函数二次项系数
- p向量存储的是目标函数一次项系数(如果有)
- A矩阵中存储的是条件式中的一次项系数
- c向量存储的是条件式中的常数项
接下来,只要将原始问题和u,Q,p,A,c一一对应上
接下来就是将相应的u,Q,p,A,c代入二次规划软件从而得到最优解
以上是比较普遍的QPsolver的做法,实际使用的QPsolver跟此方法可能会有微小的差别。比如我们接下来要讲的MATLAB软件中的quadprog函数。
4.1.1 使用MATLAB解决二次规划问题
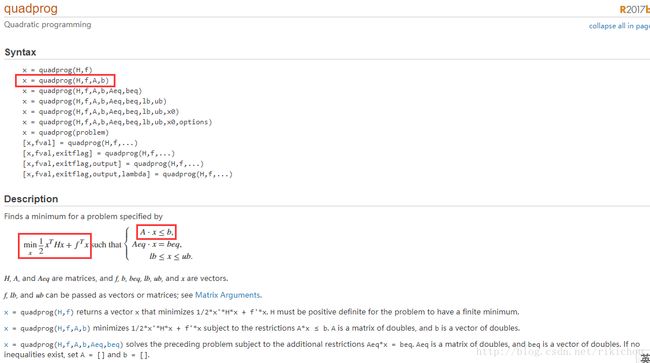
首先肯定是要看一下在MATLAB中这个函数quadprog是怎么用的咯。如下图:
在描述部分我们可以看出,该QPsolver和我们4.1节讲的大致一致,
- H就是我们的二次系数矩阵Q
- f对应于一次系数矩阵p
- A对应于条件式的一次系数矩阵A,只不过MATLAB中使用的使用A.x <= b,SVM中使用的是A.x >= b,所以只需要将SVM中的A矩阵中乘上一个-1即可
- b对应于条件式中的常数向量c。同理,也只需要将SVM中的c向量乘以-1即可。
- 返回值x表示我们的u向量,也就是[w, b]组成的最佳解。fval表示w,b取最佳解时的函数值。
由于我们的SVM中没有更多的条件,所以是需要调用x = quadprog(H,f,A,b)即可。下面通过一个例子来说明:
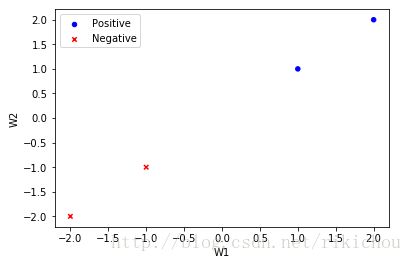
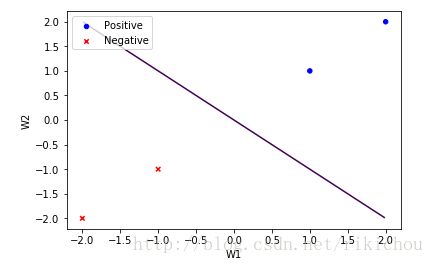
假如我们有4个线性可分的二维的data:
- x1=(1,1), y1 = 1
- x2=(2,2), y2 = 1
- x3=(-1,-1), y3 = -1
- x4=(-2,-2), y4 = -1
通过上述关系,我们很容易得出MATLAB中quadprog的H,f,A,b参数分别为
然后,直接运行quadprog()得出
我们可知b = 0, w0 = 0.5, w1 = 0.5,很明显这是我们想要的分割面,且x1和x3为支持向量。
5. 小结
我们把以上所描述的演算法称为linear hard-margin SVM
- linear – 仅仅是在X空间进行的线性分割。如果想要non-linear的分割线,进行特征转换就好了Zn = φ(Xn)。
- hard-margin – 坚持数据完全正确分开,不可以有任何违反边界的地方