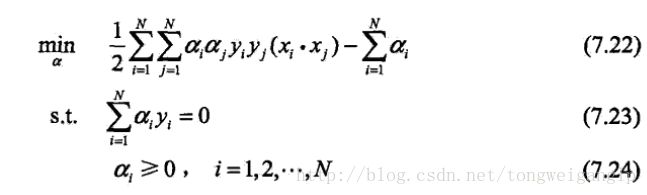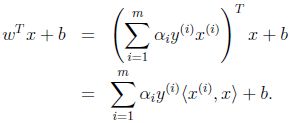第11章,从感知机到支持向量机
参考:
http://mp.weixin.qq.com/s?__biz=MzIxMjAzNDY5Mg==&mid=400067748&idx=1&sn=9c88eadfba5462281cd496e85ba3329c&scene=21#wechat_redirect
http://blog.csdn.net/v_july_v/article/details/7624837
https://www.zhihu.com/question/21094489
《统计学习方法》
https://www.zhihu.com/question/19967778/answer/184073198
1,感知机(perceptron)
感知机是最简单的神经元模型,由科学家Frank Rosenblatt发明于1950至1960年代,他受到了来自Warren McCulloch 和Walter Pitts的更早工作的启发。
感知机的工作原理如下:
![]()
输入量: x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3
权重: w 1 , w 2 , w 3 w_1,w_2,w_3 w1,w2,w3
阈值:threshold
输出量:0 or 1

变换,令b≡-threshold
所以,可以理解为感知机是一个线性分类器:f(x) = wx+b
该线性分类器由超平面 wx+b=0 进行划分。
2,线性硬间隔支持向量机
当我们的样本是完全的线形可分时,我们介绍最简单的一种支持向量机,
(1)改进
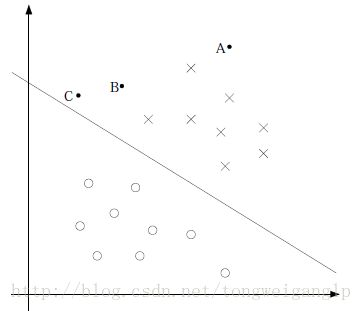
根据上图中感知机的超平面可以引出下面几个问题:
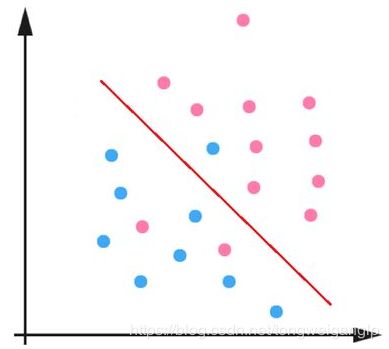
- 样本可以完全的被超平面划分,所以是线形可分的
- 更改w、b的取值,我们可以得到无数多个超平面f(x)。即只要保证X点都在超平面上方,O点都在下方即可;
- 那么如何挑选最优的那一个超平面呢?即超平面与最近的C点距离多远算事最优的呢?
- 最大化几何间隔找出最优超平面
(2) 函数间隔与几何间隔
.1) 几何间隔

假设图中超平面:f(x) = wx+b=0
则,w是其法向量:
因为假设在超平面上任意的两个点x1,x2,则
wx1=-b
wx2=-b
=> w(x1-x2)=0
又因(x1-x2) 是超平面上的任意向量,根据法向量定义,可知 w ⃗ \vec{w} w是超平面的法向量。
令 r ^ \hat{r} r^表示任意点x到超平面的距离,则,
x − x 0 = r ^ ∗ w ∣ ∣ w ∣ ∣ x-x_0=\hat{r}*\frac{w}{||w||} x−x0=r^∗∣∣w∣∣w …(1)
其中,
x − x 0 x-x_0 x−x0是向量的坐标表示法
r ^ ∗ w ∣ ∣ w ∣ ∣ \hat{r}*\frac{w}{||w||} r^∗∣∣w∣∣w是单位向量乘以长度的表示法
又因为 w x 0 + b = 0 wx_0+b=0 wx0+b=0,则对方程(1)两边均乘以w时,有
w x − w x 0 = w r ^ ∗ w ∣ ∣ w ∣ ∣ = r ^ ∗ ∣ ∣ w ∣ ∣ 2 ∣ ∣ w ∣ ∣ wx-wx_0=w\hat{r}*\frac{w}{||w||}=\hat{r}*\frac{||w||^2}{||w||} wx−wx0=wr^∗∣∣w∣∣w=r^∗∣∣w∣∣∣∣w∣∣2
w x + b = r ^ ∗ ∣ ∣ x ∣ ∣ wx+b=\hat{r}*||x|| wx+b=r^∗∣∣x∣∣,最终得到任意点到超平面距离(几何间隔)为,
r ^ = w x + b ∣ ∣ w ∣ ∣ \hat{r}=\frac{wx+b}{||w||} r^=∣∣w∣∣wx+b
.2) 函数间隔
我们是用超平面f(x) = wx+b来预测y值的。
感知机时,y值的标记是0或1,此处我们变换一下,当f(x)>=0时,y=1,f(x)<0时,y=-1。作为二分类的不同标记方式,并不影响结果。
我们定义一个函数间隔 r,
r = y ∗ f ( x ) = y ( w x + b ) = ∣ w x + b ∣ r=y*f(x) = y(wx+b)=|wx+b| r=y∗f(x)=y(wx+b)=∣wx+b∣
从定义上我们可知,几个间隔=函数间隔/||w||
则,函数间隔的几何意义表示任意一个点到超平面点距离的||w||倍
当我们限制法向量的长度为1,即 ∣ ∣ w ∣ ∣ = 1 ||w||=1 ∣∣w∣∣=1时,函数间隔=几何间隔
(3)最优目标
我们的最优目标是希望能够找到一个超平面,能够分割两类的点,并且这个超平面距离两类最近的点的间隔都是一样的远。
距离两类最近的点即为“支持向量”。
两类支持向量到超平面的几何间隔是一样的,我们的目标,就是想让支持向量到超平面的几何间隔( r ^ \hat{r} r^ )最大化,即
max r ^ \hat{r} r^
s.t. y i ( w x i + b ) ∣ ∣ w ∣ ∣ > = r ^ \frac{y_i(wx_i+b)}{||w||}>=\hat{r} ∣∣w∣∣yi(wxi+b)>=r^
上式中,最大化几何间隔,可以改写为最大化函数间隔
max r ∣ ∣ w ∣ ∣ \frac{r}{||w||} ∣∣w∣∣r
s.t. y i ( w x i + b ) > = r y_i(wx_i+b)>=r yi(wxi+b)>=r
我们再来考虑一个问题:
令函数间隔为一个常数,是否可行?
函数间隔实际上是等于|wx+b|的,那么不论|wx+b|等于什么,只要w和b同比例放大或缩小之后,都可以让|wx+b|=1成立。所以,当我们研究目标函数最大或最小值时,等比例的问题是不影响求解最优值的。C为常数时,max(Cx)=Cmax(x)
于是为了简化求解方程,我们令函数间隔为1,即,我们会得到两个关于f(x)=0对称的超平面,如下所示:

于是,我们的优化问题又变为
max 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1
s.t. y i ( w x i + b ) > = 1 y_i(wx_i+b)>=1 yi(wxi+b)>=1
其中, 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1 为超平面f(x)=1到f(x)=0的几何距离
即,我们研究点最优解点目标为,最大化|f(x)|=1的两个对称超平面之间的间隔,并且支持向量会落在这两个超平面上。
最后,又因为最大化 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1与最小化 1 2 ∣ ∣ w ∣ ∣ 2 \frac{1}{2}||w||^2 21∣∣w∣∣2是等价的,最终我们得到求解目标为:
min 1 2 ∣ ∣ w ∣ ∣ 2 \frac{1}{2}||w||^2 21∣∣w∣∣2
s.t. y i ( w x i + b ) > = 1 y_i(wx_i+b)>=1 yi(wxi+b)>=1
现在的目标函数是二次的,约束条件是线性的,所以目标问题是一个凸二次规划问题
引入拉格朗日算子 a i {a_i} ai ,我们有:
L ( w , b , a ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ a i y i ( w x i + b ) + ∑ a i L(w,b,a)=\frac{1}{2}||w||^2-\sum{a_iy_i(wx_i+b)}+\sum{a_i} L(w,b,a)=21∣∣w∣∣2−∑aiyi(wxi+b)+∑ai (7.18)
求解过程:
原始问题的对偶问题为, M a x ( a ) M i n ( w , b ) ( L ( w , b , a ) ) Max_{(a)}Min_{(w,b)}(L(w,b,a)) Max(a)Min(w,b)(L(w,b,a))
先求解 θ = M i n ( w , b ) ( L ( w , b , a ) ) θ=Min_{(w,b)}(L(w,b,a)) θ=Min(w,b)(L(w,b,a))
再求解 M a x ( a ) θ Max_{(a)}θ Max(a)θ
M a x ( a ) θ Max_{(a)}θ Max(a)θ= M i n ( a ) ( − θ ) Min_{(a)}(-θ) Min(a)(−θ),即我们求
我们可以得到a的解.
此处,我们把x表示成向量内积的形式,为核变换做准备。
3,线性软间隔支持向量机
(1)改进
“线性硬间隔支持向量机”的假设是数据线性可分,但是当数据是线性不可分的时候要如何处理呢?
- 硬间隔最大化 -> 变成软间隔最大化
线性不可分意味着,并不是所有的点都能够满足:大于等于支持向量的几何间隔(即1).因此我们对每个样本 ( x i , y i ) (x_i,y_i) (xi,yi)引入了松弛变量 ε i > = 0 ε_i>=0 εi>=0
y i ( w x i + b ) > = 1 − ε i y_i(wx_i+b)>=1-ε_i yi(wxi+b)>=1−εi
同时对每一个松弛变量都支付一个代价,目标函数变为:
1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ ε i \frac{1}{2}||w||^2+C\sum{ε_i} 21∣∣w∣∣2+C∑εi
此处,C称作惩罚参数,对代价有调节的作用。
min 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ ε i \frac{1}{2}||w||^2+C\sum{ε_i} 21∣∣w∣∣2+C∑εi
s.t. y i ( w x i + b ) > = 1 − ε i y_i(wx_i+b)>=1-ε_i yi(wxi+b)>=1−εi
ε i > = 0 ε_i>=0 εi>=0
可以证明w的解是存在的且唯一,但是b的值不是唯一的,存在一个区间。
根据硬间隔支持向量机的推到,可以得到:

4,Hilbert空间
- 1).线性空间
线性空间又称作向量空间,关注的是向量的位置,对于一个线性空间,知道基(相当于三维空间中的坐标系)便可确定空间中元素的坐标(即位置);线性空间只定义了加法和数乘运算。如果我们想知道向量的长度怎么办?—-定义范数,引入赋范线性空间 - 2).赋范线性空间定义了范数的线性空间
如果我们想知道向量的夹角怎么办?—-定义内积,引入内积空间 - 3).内积空间定义了内积的线性空间。
- 4).欧式空间定义了内积的有限维实线性空间。如果我们想研究收敛性(极限)怎么办?—-定义完备
- 5).Hilbert空间完备的内积空间
5,核函数定义
如果数据集线性不可分,那么把数据集映射到高维特征空间后,往往是线性可分的。比如说,m维的数据,在m-1维空间中,往往可以被超平面线性可分。
所以说,把数据映射到高维空间是有好处的。
假设我们定义了一个高维的映射,但是联想到我们“线性硬间隔svm算法中的内积形式”,可知,这种高维映射后的内积的计算量比较大的。
那么有没有一种高维的映射,使得映射后的向量内积直接等于一个固定形式呢?
如果有,那么这种隐式的映射会大大减少计算量。(所谓隐式,是因为我们只需要知道映射到高维的内积的具体形式及结果即可,不需要中间映射后的高维向量本身) 这就引出了我们要介绍的核函数。
核函数
假设X是输入空间(欧式空间),H是特征空间(Hilbert空间),如果存在一个X到H到映射:
θ ( x ) : X − > H θ(x):X->H θ(x):X−>H
对于所有x,z ∈ X,函数K(x,z) 满足条件
K(x,z)=θ(x)θ(z)
则称K(x,z)为核函数,θ(x)为映射函数,核函数等于映射的内积
备注:特征空间一般是高维的,甚至是无穷维的
所以,给定和函数,把线性svm求解中的向量内积全部替换成核函数,即可隐式的实现,用线性分类的方法求解非线性问题。学习是隐式的在特征空间内进行的,这样的技巧称为核技巧。
6,常用核函数
-
线性核函数
θ ( x ) = x , K ( X , X ′ ) = X T X ′ θ(x)=x,K(X,X')=X^TX' θ(x)=x,K(X,X′)=XTX′ -
多项式核函数
K ( x , x i ) = ( x x i + 1 ) q K(x,x_i)=(xx_i+1)^q K(x,xi)=(xxi+1)q -
高斯径向基核函数
K ( x , x i ) = e x p { − ∣ ∣ x − x i ∣ ∣ 2 σ 2 } K(x,x_i)=exp\{-\frac{||x-x_i||}{2σ^2}\} K(x,xi)=exp{−2σ2∣∣x−xi∣∣} -
Sigmoid核函数
K ( x , x i ) = t a n h ( v ( x x i ) + c ) K(x,x_i)=tanh(v(xx_i)+c) K(x,xi)=tanh(v(xxi)+c) -
字符串核