支持向量机 （SMO算法原理与简化版实现）

SMO算法原理及实现

支持向量机的学习问题本质上是求解凸二次规划问题
SMO算法 序列最小最优化算法就是求解该问题的代表性算法
SMO算法 解决的凸二次规划的对偶问题:
mina12∑i=1N∑j=1NαiαjyiyjK(xi,xj)−∑i=1Nαi min a 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( x i , x j ) − ∑ i = 1 N α i
s.t.∑i=1Nαiyi=00≤αi≤C,i=1,2,...,N s . t . ∑ i = 1 N α i y i = 0 0 ≤ α i ≤ C , i = 1 , 2 , . . . , N
问题思考:已知变量 x 输入空间 y 输入空间 – 即训练集中数据集
求解变量实质上为拉格朗日乘子 一个变量 αi α i 对应与一个样本点 (xi,yi) ( x i , y i ) ,变量的总数等于训练样本容量N

SMO算法 – 属于一种启发式算法

其基本思路为:
1.如果所有的变量的解都满足最优化问题的KKT条件 那么这个最优化问题的解就得到了
2.否则选择两个变量 固定其他变量(任意选择两个拉格朗日乘子) 针对这两个变量构建一个二次规划问题
这个二次规划问题关于这两个变量的解应该更加接近二次规划问题的解 使得二次规划问题的目标函数值变得更小
3.此时: 子问题有两个变量 一个是违反KKT条件最严重的一个 一个是由约束条件自动确定的

注意: 选择两个变量实质上只有一个自由变量
因为等式约束:
∑i=2Nαiyi=0 ∑ i = 2 N α i y i = 0

重点:SMO算法实质上包含两个部分
1. 求解两个变量二次规划的解析方法
2.选择变量的启发式方法

1.两个变量二次规划的求解方法

假设选择的两个变量是 α1,α2 α 1 , α 2 其他 αi α i 是固定的
带入到凸二次规划的对偶问题中, 可以推导为
minalpha1,α2=12K11α21+12K22α22+y1y2K12α1α2−(α1+alpha2)+y1alpha1∑i=3NyiαiKi1+y2α2∑i=3NyiαiK12s.t.a1y1+a2y2=−∑i=3Nyiαi=ξ0≤αi≤C,i=1,2 min a l p h a 1 , α 2 = 1 2 K 1 1 α 1 2 + 1 2 K 2 2 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + a l p h a 2 ) + y 1 a l p h a 1 ∑ i = 3 N y i α i K i 1 + y 2 α 2 ∑ i = 3 N y i α i K 12 s . t . a 1 y 1 + a 2 y 2 = − ∑ i = 3 N y i α i = ξ 0 ≤ α i ≤ C , i = 1 , 2
其中Kij=K(xi,xj),i,j=1,2,..,N,ξ为常数 其 中 K i j = K ( x i , x j ) , i , j = 1 , 2 , . . , N , ξ 为 常 数

为了求解两个变量的二次规划问题, 首先分析约束条件 然后再次约束条件中求极小值

如图：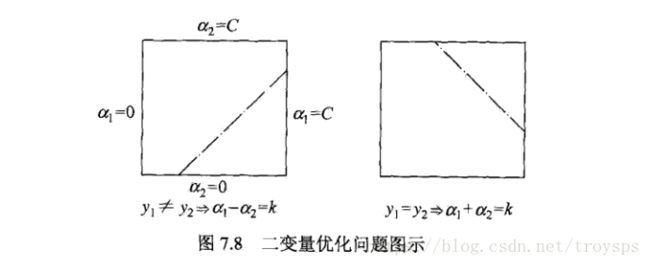
假设问题的初始解为 alphaold1,αold2 a l p h a 1 o l d , α 2 o l d , 最优解为 alphanew1,αnew2 a l p h a 1 n e w , α 2 n e w
该条件需要满足约束条件, 并假设沿着约束方向未经剪辑时 α2 α 2 的最优解为 αnew2 α 2 n e w $

即: L≤αnew2≤H L ≤ α 2 n e w ≤ H
当 y1!=y2 y 1 ! = y 2 时, 异侧相减
L=max(0,αold2−αold1),H=min(C,C+αold2−αold1 L = m a x ( 0 , α 2 o l d − α 1 o l d ) , H = m i n ( C , C + α 2 o l d − α 1 o l d
当 y1==y2时 y 1 == y 2 时 , 同侧相加
L=max(0,αold2+αold1−C),H=min(C,αold2+αold1) L = m a x ( 0 , α 2 o l d + α 1 o l d − C ) , H = m i n ( C , α 2 o l d + α 1 o l d )

满足约束条件之后, 沿着约束方向更新 α2 α 2
首先求 αold1,αold2 α 1 o l d , α 2 o l d 的预测值 与实际值之间的误差
Ei=g(xi)−yi=∑j=1NαjyjK(xj,xi)+b)−yi,i=1,2 E i = g ( x i ) − y i = ∑ j = 1 N α j y j K ( x j , x i ) + b ) − y i , i = 1 , 2

定理: 最优化问题沿约束方向未经剪辑时的解是:
αnew2=αold2+y2(E1−E2)η其中:η=K11+K22−2K12=||K(x1)−K(x2)||2 α 2 n e w = α 2 o l d + y 2 ( E 1 − E 2 ) η 其 中 : η = K 1 1 + K 2 2 − 2 K 1 2 = | | K ( x 1 ) − K ( x 2 ) | | 2

2.变量的选择方式

SMO算法在每个子问题中选择两个变量优化 其中至少一个变量是违反KKT条件的
1.第1个变量的选择
选择第1个变量的过程为外层循环 外层循环在训练样本中选取违反KKT条件最严重的样本点
并将其对应的变量作为第1个变量 –> 即:检验训练样本点 (xi,yi) ( x i , y i ) 是否满足KKT条件
KKT条件为:
αi=0==>yig(xi)≥10<αi<C===>yig(xi)=1αi=C==>yig(xi)≤1 α i = 0 ==> y i g ( x i ) ≥ 1 0 < α i < C ===> y i g ( x i ) = 1 α i = C ==> y i g ( x i ) ≤ 1
其中 g(xi)=∑j=1NαjyjK(xi,xj)+b g ( x i ) = ∑ j = 1 N α j y j K ( x i , x j ) + b
2.第2个变量的选择
选择第2个变量为内层循环 假设在外层循环中以及找到第一个变量 α1 α 1 ,现在要在内层循环中找到第2个变量，第二个变量的选择标准是
希望能使 α2 α 2 有足够的变化
使得 alpha2 a l p h a 2 的取值满足约束条件,由之前推导可得更新 alpha2 a l p h a 2 条件是:1.满足二次规划问题 2.根据 |E1−E2| | E 1 − E 2 | 更新 α2 α 2

伪代码基本逻辑为:
1.如果内层循环通过以上方法选择的 α2 α 2 不能使得目标函数有足够的下降 那么采用启发式规则继续选择 α2 α 2
2.遍历在间隔边界上的支持向量点 依次将其对应的变量作为 α2 α 2 试用 直到目标函数有足够的下降
3.若是仍然找不到合适的 α2 α 2 , 则放弃第一个 alpha1 a l p h a 1 ,再通过外层循环找另外的 alpha1 a l p h a 1

3.计算阈值b与差值 Ei E i
每次完成两个变量的优化后 都要重新计算阈值b, 由KKT条件可知
∑i=1NαiyiKi1+b=y1 ∑ i = 1 N α i y i K i 1 + b = y 1
于是:
bnew1=y1−∑i=3NαiyiKi1−αnew1y1K11−αnew2y2K21 b 1 n e w = y 1 − ∑ i = 3 N α i y i K i 1 − α 1 n e w y 1 K 11 − α 2 n e w y 2 K 21
由 E1 E 1 的定义式有:
E1=∑i=3NαiyiKi1+αold1y1K11+αold2y2K21+bold−y1 E 1 = ∑ i = 3 N α i y i K i 1 + α 1 o l d y 1 K 1 1 + α 2 o l d y 2 K 2 1 + b o l d − y 1
即可得:
bnew1=−E1−y1K11(αnew1−αold1−y2K21(αnew2−αold2)+bold b 1 n e w = − E 1 − y 1 K 11 ( α 1 n e w − α 1 o l d − y 2 K 21 ( α 2 n e w − α 2 o l d ) + b o l d

SMO算法伪代码实现

创建一个 alpha 向量并将其初始化为0向量
当迭代次数小于最大迭代次数时(外循环)
    对数据集中的每个数据向量(内循环)：
        如果该数据向量可以被优化
            随机选择另外一个数据向量
            同时优化这两个向量
            如果两个向量都不能被优化，退出内循环
    如果所有向量都没被优化，增加迭代数目，继续下一次循环

简化版SMO算法实现

import numpy as np
import matplotlib.pyplot as plt


def loadDataSet(fileName):
    """
    对文件进行逐行解析，从而得到第行的类标签和整个特征矩阵
    Args:
        fileName 文件名
    Returns:
        dataMat  特征矩阵
        labelMat 类标签
    """
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat

def selectJrand(i, m):
    """

    :param i:  alpha i index
    :param m:  dataMat m dimension
    :return: j

    """
    while True:
        j = int(np.random.uniform(m))
        if j != i:
            return j

def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if aj < L:
        aj = L
    return aj

def smoSimple(dataMat, labelMat, C, toler, maxCycle):
    """

    :param dataMat:    数据的输入空间
    :param labelMat:   数据的输出空间
    :param C:          常量值 松弛变量
    :param toler:      容错率
    :param maxCycle:   最大迭代次数
    :returns
        b        模型的常量值
        alphas   拉格朗日乘子法
    """

    # 输入空间 矩阵化
    dataMatrix = np.mat(dataMat)
    # 输出空间 矩阵化
    labelMat = np.mat(labelMat).transpose()

    # 获取样本数据集 样本数m 维度n
    m, n = np.shape(dataMatrix)

    # 初始化b 以及 拉格朗日参数alphas

    b = 0
    # 对每一输入数据 都有一个拉格朗日参数alpha 初始化alphas 为mx1维度的矩阵
    alphas = np.mat(np.zeros((m, 1)))
    print(np.shape(alphas))

    # 记录循环
    iter = 0
    while (iter < maxCycle):
        # 记录alpha参数是否优化
        alphaPairsChanged = 0
        for i in range(m):

            # 计算alpha[i] 的预测值 与 误差值
            # 将负责的问题转化为 二阶问题 抽取 alphas_i alphas_j 进行优化 将大问题转为小问题
            predXi = float(np.multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[i, :].T)) + b
            # print(predXi)
            Ei = predXi - float(labelMat[i])
            # print(Ei)

            """kkt 详解"""
            # 约束条件 (KKT条件是解决最优化问题的时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值)
            # 0<=alphas[i]<=C，但由于0和C是边界值，我们无法进行优化，因为需要增加一个alphas和降低一个alphas。
            # 表示发生错误的概率：labelMat[i]*Ei 如果超出了 toler， 才需要优化。至于正负号，我们考虑绝对值就对了。
            '''
            # 检验训练样本(xi, yi)是否满足KKT条件
            yi*f(i) >= 1 and alpha = 0 (outside the boundary)
            yi*f(i) == 1 and 0
            # 不满足kkt条件进行优化
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                # print('需要进行优化')

                # 随机抽取非i 的alphas j
                j = selectJrand(i, m)

                # print('i:{} j:{}'.format(i, j))

                # 计算alphas j 的预测值与误差值
                predXj = float(np.multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[j, :].T)) + b
                print('predXj', predXj)
                Ej = predXj - float(labelMat[j])
                # 记录未优化前的alphas[i] 与 alphas[j] 值
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()

                # 二变量优化问题
                if (labelMat[j] != labelMat[i]):
                    # \sum ai * yi = k
                    # 如果是异侧 相减 ai-aj=k   那么 定义域为 [k, C + k]
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    # 同侧 相加 ai + aj=k 那么定义域为 [k-c, k]
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])

                # 定义与确定就没有优化空间了 跳出循环
                if L == H:
                    print("没有优化空间 定义域确定")
                    continue

                # 对alphas[j] 进行优化

                # 首先计算其 eta值 eta=2*ab - a^2 - b^2  如果eta>=0那么跳出循环 是正确的
                eta = 2.0*dataMatrix[i, :]*dataMatrix[j, :].T - dataMatrix[i, :]*dataMatrix[i, :].T - dataMatrix[j, :]*dataMatrix[j,:].T
                if eta>=0:
                    print('eta>=0')
                    continue
                # 计算出一个新的alphas[j]值

                print('eta', eta)
                print('Ei', Ei)
                print('Ej', Ej)

                print(labelMat[j]*(Ei - Ej)/eta)
                print(alphas[j])
                # 优化新aj值 aj = yj * (ei-ej)/eta
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta

                # 使用辅助函数调整alphas[j] aj在定义域中
                alphas[j] = clipAlpha(alphas[j], H, L)

                # 检查alphaJ 调整幅度对比 比较小就退出
                if (abs(alphas[j] - alphaJold) < 0.00001):
                    print("j not moving enough")
                    continue

                # 同时优化alpha[i] 优化了aj 那么同样优化 ai += yj*yi(aJ_old - aj)
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                # 分别计算模型的常量值
                # bi = b - Ei - yi*(ai - ai_old)*xi*xi.T - yj(aj-aj_old)*xi*xj.T
                # bj = b - Ej - yi*(ai - ai_old)*xi*xj.T - yj(aj-aj_old)*xj*xj.T
                b1 = b - Ei - labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[i, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i, :]*dataMatrix[j, :].T
                b2 = b - Ej - labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[j, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j, :]*dataMatrix[j, :].T
                # 判断哪个模型常量值符合 定义域规则 不满足就 暂时赋予 b = (bi+bj)/2.0
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
        # 在for循环外，检查alpha值是否做了更新，如果在更新则将iter设为0后继续运行程序
        # 知道更新完毕后，iter次循环无变化，才推出循环。
        if (alphaPairsChanged == 0):
            iter += 1
        else:
            iter = 0
        print("iteration number: %d" % iter)
    return b, alphas


def calcWs(alphas, dataArr, classLabels):
    """
    基于alpha计算w值
    Args:
        alphas        拉格朗日乘子
        dataArr       feature数据集
        classLabels   目标变量数据集
    Returns:
        wc  回归系数
    """
    X = np.mat(dataArr)
    labelMat = np.mat(classLabels).transpose()
    m, n = np.shape(X)
    w = np.zeros((n, 1))
    for i in range(m):
        w += np.multiply(alphas[i] * labelMat[i], X[i, :].T)
    print('w', w)
    return w


def plotfig_SVM(xMat, yMat, ws, b, alphas):
    """
    参考地址：
       http://blog.csdn.net/maoersong/article/details/24315633
       http://www.cnblogs.com/JustForCS/p/5283489.html
       http://blog.csdn.net/kkxgx/article/details/6951959
    """

    xMat = np.mat(xMat)
    yMat = np.mat(yMat)

    # b原来是矩阵，先转为数组类型后其数组大小为（1,1），所以后面加[0]，变为(1,)
    b = np.array(b)[0]
    fig = plt.figure()
    ax = fig.add_subplot(111)

    # 注意flatten的用法
    ax.scatter(xMat[:, 0].flatten().A[0], xMat[:, 1].flatten().A[0])

    # x最大值，最小值根据原数据集dataArr[:, 0]的大小而定
    x = np.arange(-1.0, 10.0, 0.1)

    # 根据x.w + b = 0 得到，其式子展开为w0.x1 + w1.x2 + b = 0, x2就是y值
    y = (-b-ws[0, 0]*x)/ws[1, 0]
    ax.plot(x, y)

    for i in range(np.shape(yMat[0, :])[1]):
        if yMat[0, i] > 0:
            ax.plot(xMat[i, 0], xMat[i, 1], 'cx')
        else:
            ax.plot(xMat[i, 0], xMat[i, 1], 'kp')

    # 找到支持向量，并在图中标红
    for i in range(100):
        if alphas[i] > 0.0:
            ax.plot(xMat[i, 0], xMat[i, 1], 'ro')
    plt.show()

def main():
    filename = 'testSet.txt'
    dataMat, labelMat = loadDataSet(filename)


    b, alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)


    ws = calcWs(alphas, dataMat, labelMat)
    plotfig_SVM(dataMat, labelMat, ws, b, alphas)

if __name__ == '__main__':
    main()

参考文献
《李航统计学习方法》，李航
《机器学习实战》， Peter