2019独角兽企业重金招聘Python工程师标准>>> ![]()
一、逆波兰表达式
1.中缀表达式
中缀表达式表示操作符、运算符在需要计算的数值中间
比如:(1-2)*(4+5)
但是计算机不喜欢这样的,因为表达式中有小括号中括号大括号,还允许一个嵌套一个,这样子计算机就要进行很多次if判断才能决定先计算哪里,而且需要使用到递归,所以计算机计算这个效率就非常低。
2.逆波兰表达式
在20世纪30年代,波兰逻辑学家Jan.Lukasiewicz发明了一种不需要括号的后缀表达式,我们通常把它称为逆波兰表达式(RPN),逆波兰表达式也叫后缀表达式。
比如:(1-2)*(4+5),用逆波兰表达式表示法,则是 1 2 - 4 5 + *
- 虽然这种表示方法对于人类思维不太好接受,但是对于计算机可谓喜爱至极;
- 因为只需要利用栈的特点,就可以将这种后缀表达式的性能发挥到极致。
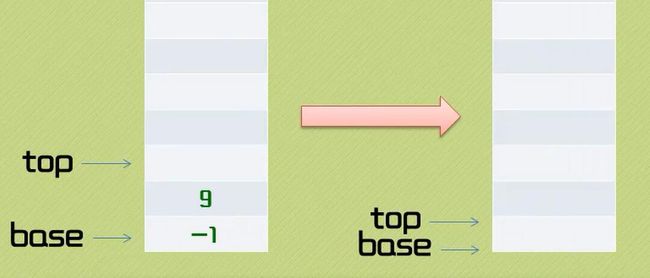
我们通过图片来看看通过栈是如何实现的:
(1)数字1和2进栈,遇到减号运算符则弹出两个元素进行运算并把结果-1入栈;
(2)4和5入栈,遇到加号运算符,4和5弹出栈,相加后将结果9入栈;
(3)将9和-1弹出栈进行乘法运算,此时栈空并无数据压栈,-9即为最终运算结果。
3.代码实现逆波兰计算器
#include
#include
#include
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
#define MAXBUFFER 10
typedef double ElemType;
typedef struct{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
// 创建一个栈
void InitStack(sqlStack *s){
s->base = (ElemType *)malloc(STACK_INIT_SIZE *sizeof(ElemType));
if(!s->base){
exit(0);
}
s->top = s->base;
s->stackSize = STACK_INIT_SIZE;
}
// 压栈
void Push(sqStack *s, ElemType e){
if(s->top - s->base >= s->stackSize){
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT)*sizeof(ElemType));
if(!s->base){
exit(0);
}
}
*(s->top) = e;
s->top++;
}
void Pop(sqStack *s, ElemType *e){
if(s->top == s->base){
return;
}
*e = *--(s->top);
}
// 计算栈的当前容量
int StackLen(sqStack s){
return (s.top - s.base);
}
double main(){
sqStack s;
char c;
double d, e;
char str[MAXBUFFER];
InitStacke(&s);
printf("请按逆波兰表达式输入待计算数据,数据与运算符之间用空格隔开,以#号作为结束标志:\n");
scanf("%c", &c);
while(C != '#'){
while(isdigit(c) || c=='.'){ // 用于过滤数字
str[i++] = c;
str[i] = '\0';
if(i>=10){
printf("出错:输入的单个数据过大!\n");
return -1;
}
scanf("%c", &c);
if(c == ' '){
d = atof(str);
Push(&s, d);
i = 0;
break;
}
}
switch(c){
case '+':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d+e);
break;
case '-':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d-e);
break;
case '*':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d*e);
break;
case '/':
Pop(&s, &e);
Pop(&s, &d);
if(e != 0){
Push(&s, d/e);
}else{
printf("\n出错:除数为零!\n");
return -1;
}
break;
}
scanf("%c", &c);
}
Pop(&s, &d);
printf("\n最终的计算结果为:%f\n", d);
return 0;
}
// 计算案例
// 1 2 - 4 5 + * 结果:9.000000
// 5 - (6 + 7) * 8 + 9 / 4 5 6 7 + 8 * - 9 4 / + 结果:-96.750000
本文为原创文章,如果对你有一点点的帮助,别忘了点赞哦!比心!如需转载,请注明出处,谢谢!