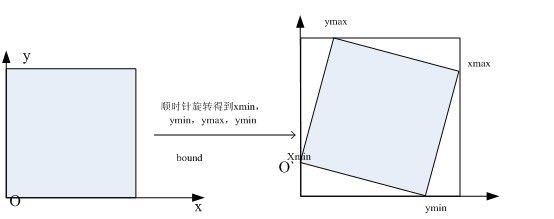
需求:对每个新图像中的像素进行遍历。计算像素点在原图像中对应的位置。
由于在求边界时,假定图像进行顺时针旋转,因此此处进行反推新像素位置在原图像中的对应位置时,需要用逆时针计算。
顺时针计算方法是:
X = xcos(theta) + y sin(theta)
Y = y cos(theta) – x sin(theta)
逆时针计算方法是:
X= x cos(theta) – ysin(theta)
Y = xsin(theta) + ycos(theta)。
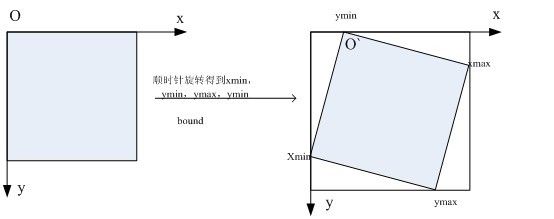
而图像的坐标轴与平常所用的坐标轴不同。
也就是说,图像的旋转顺时针和逆时针的坐标变换公式与常见坐标的变换公式相反:
逆时针计算方法是:
X = xcos(theta) + y sin(theta)
Y = y cos(theta) – x sin(theta)
顺时针计算方法是:
X= x cos(theta) – ysin(theta)
Y = xsin(theta) + ycos(theta)。
边界xmin,xmax,ymin,ymax的计算方法:
void bound(int x, int y, float ca, float sa, int *xmin, int *xmax, int *ymin, int *ymax)
/* int x,y;
float ca,sa;
int *xmin,*xmax,*ymin,*ymax;*/
{
int rx,ry;
// 以左上角为中心逆时针旋转
rx = (int)floor(ca*(float)x+sa*(float)y);
ry = (int)floor(-sa*(float)x+ca*(float)y);
if (rx<*xmin) *xmin=rx; if (rx>*xmax) *xmax=rx;
if (ry<*ymin) *ymin=ry; if (ry>*ymax) *ymax=ry;
}
计算出边界来之后,就可以用下式子计算出新图像的高度和宽度。
xmin = xmax = ymin = ymax = 0;
bound(nx-1,0,ca,sa,&xmin,&xmax,&ymin,&ymax);
bound(0,ny-1,ca,sa,&xmin,&xmax,&ymin,&ymax);
bound(nx-1,ny-1,ca,sa,&xmin,&xmax,&ymin,&ymax);
sx = xmax-xmin+1;
sy = ymax-ymin+1;
然后就可以利用cvWarpAffine( src, rotImage, &M,CV_INTER_LINEAR+CV_WARP_FILL_OUTLIERS,
cvScalarAll(0) )进行旋转。
其实,方法cvWarpAffine看起来的效果,貌似是按照图像左上角旋转,然后,平移矩阵a13,a23得到的。
即:
xp = ca * x + sa * y - xtrans;
yp = ca * y – sa * x - ytrans;
M矩阵为:
m[0] = ca;
m[1] = sa;
m[2] =-(float)xmin;
m[3] =-m[1];
m[4] = m[0];
m[5] =-(float)ymin;
绕了好几天,终于搞清楚了。
上文中提到的都是从原图计算旋转后新图的问题。
怎样进行复原。
首先,需要找出原图像的原点。此处就是原图像左上角的点,在新图像中的位置。旋转超过90°和不超过需要分开处理。
void compensate_affine_coor1(int *x0, int *y0, int w1, int h1, float t1, float t2, float Rtheta)
{
// 逆时针旋转时的复原
float x_ori, y_ori;
float x_tmp, y_tmp;
float x1 = *x0;
float y1 = *y0;
Rtheta = Rtheta*CV_PI/180;
if ( Rtheta <= CV_PI/2 )
{
x_ori = 0;
y_ori = w1 * sin(Rtheta) / t1;
}
else
{
x_ori = -w1 * cos(Rtheta) / t2;
y_ori = ( w1 * sin(Rtheta) + h1 * sin(Rtheta-CV_PI/2) ) / t1;
}
float sin_Rtheta = sin(Rtheta);
float cos_Rtheta = cos(Rtheta);
/* project the coordinates of im1 to original image before tilt-rotation transform */
/* Get the coordinates with respect to the 'origin' of the original image before transform */
x1 = x1 - x_ori;
y1 = y1 - y_ori;
/* Invert tilt */
x1 = x1 * t2;
y1 = y1 * t1;
/* Invert rotation (Note that the y direction (vertical) is inverse to the usual concention. Hence Rtheta instead of -Rtheta to inverse the rotation.) */
x_tmp = cos_Rtheta*x1 - sin_Rtheta*y1;
y_tmp = sin_Rtheta*x1 + cos_Rtheta*y1;
x1 = x_tmp+1;
y1 = y_tmp+1;
*x0 = x1;
*y0 = y1;
}
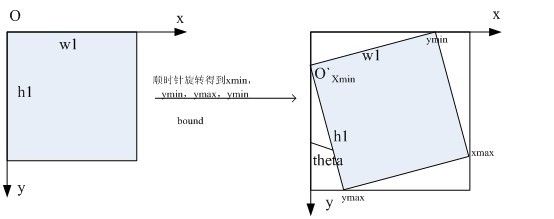
旋转不超过90度时,
因此,O`的x_ori = 0; y_ori = w1 * sin(Rtheta) / t1;
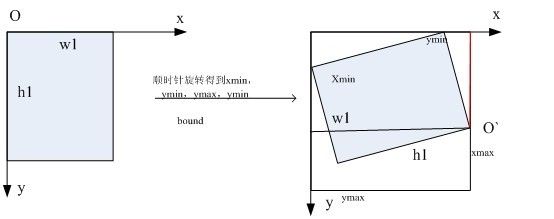
如果超过90度时,
x_ori = -w1 * cos(Rtheta) / t2;
y_ori = ( w1 * sin(Rtheta) + h1 * sin(Rtheta-CV_PI/2) ) / t1;
首先将所需要还原的坐标点平移,使之变为相对于O`点的坐标。然后,以O`点,即原来的O点按相反的方向旋转theta角度。注意,w1和h1是旋转前新图像的高宽,而不是旋转后新图像的高和宽。