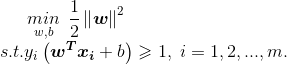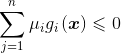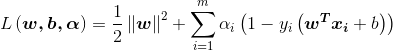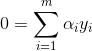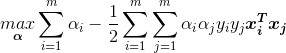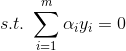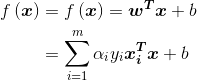二、SVM----理论推导&对偶问题、KKT条件

之所以在线性回归之后写SVM，是因为LogisticRegression可以认为是通过单调可微函数----Sigmod函数将回归问题引申为分类问题；而SVM则可以看做使用线性回归模型以及到所确定的超平面间的距离来进行分类任务。表达得不一定清晰，还是看下面的内容吧。

目录

理论推导：

对偶问题：

先写出原始问题

拉格朗日乘子法：

什么是对偶问题呢？

先定义原始问题的拉格朗日“对偶函数”

对偶函数为原始问题提供下界，引出优化问题

利用对偶函数解原始问题

KKT条件

对偶性：

为什么要用对偶问题呢？

SVM中的对偶问题

 

---

理论推导：

我们想寻找一个超平面能够将这些带有标记值的样本进行分类。而我们会得到如上图的多个划分超平面，而直观上应该去找两类样本“正中间”的划分超平面，就是红色的那个。因为在其他的超平面附近总有某一类样本离超平面距离很近，而取值与这些样本很相近的新样本就会很大概率上发生误分类。红色的超平面受影响最小，即最鲁棒性，泛化性能最好。

在样本空间中，划分超平面可通过如下线性方程描述：

                                                                                     

其中为法向量，决定了超平面的方向。为位移项，决定了超平面与原点之间的距离。超平面由和决定，记为。样本空间中任意点到超平面的距离可以写为：

                                                                                    

因为，假设超平面能够正确分类，则同一类的样本在超平面的一侧。通过放缩变化，也就是与同时乘一个系数，使得下面式子等式右边恒为1。

                                                                            

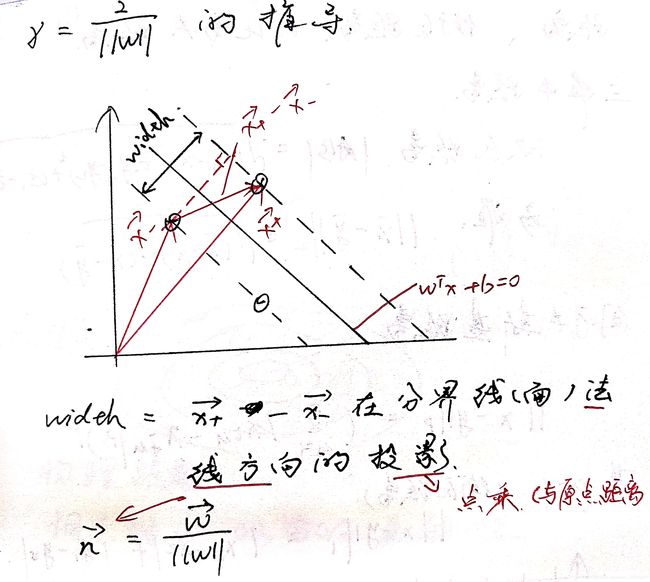
使得等号成立的样本称为“支持向量(support vector)”，简单的可以记为。两个异类支持向量到超平面的距离之和为：   。推导如下：

                                                                             

其中和都满足，解出结果并带入得

                                                                             

                                                                                 

被称为“间隔(margin)”。欲求得泛化能力最强的模型，也就是找到具有“最大间隔(maximum margin)”的划分超平面，也就是找到能够满足正确分类这一约束条件的参数和，使得最大，即：

                                                                    

也就等价于SVM基本型：

                                                                     

 

对偶问题：

先写出原始问题

                                                         

                                   等式约束：    

                                 不等式约束：  

其中定义域为、和定义域的交集，而可行域是其中满足等式与不等式约束的点。我们可以看出来原始问题约束条件   复杂，而可行域空间小。

 

拉格朗日乘子法：

拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子(只是给约束条件加了个参数而已)，可将有个变量与个约束条件的最优化问题转化为具有个变量的无约束优化问题求解。对于同时有等式和不等式约束的情况，只要再添加拉格朗日乘子即可。

引入拉格朗日乘子、，那么原始问题的拉格朗日函数为：

                                                        

现在我们得到了一个没有约束条件，但是式子变得更为复杂的一个函数，这个函数是以、和为变量。其中

                                                                    ，

现在让我们先停一下，看看我们的原始问题是什么。我们想在的定义域中找到使得最小的解。我们首先将固定住，使得是关于和的函数，求其最大值，即。

为什么要求这个最大值呢？个人的理解：若约束条件不成立，例如了，那么这样构建的拉格朗日函数的最大值将突破天际，没有上线；若全部约束条件都满足（，）,则很明显，拉格朗日函数此时的最大值就是的最大值加上后面求和的最大值。后面求和的最大值只能是0，所以的最大值就等于的最大值。

那么这个最大值也就是一个只与有关的函数。接着我们在的定义域中搜索解。也就是：

                                                                           

 

什么是对偶问题呢？

在刚在的求解思路中，我们先固定了，然后先求，再求。这是一个极小极大问题。而“对偶问题”可以简单理解为将这个顺序调换。变成极大极小问题。

                                                                           

• 先定义原始问题的拉格朗日“对偶函数”

                                      

                                                     

这里的表示寻找下确界，表示在定义域中求解。

• 对偶函数为原始问题提供下界，引出优化问题

记为可行域的点（就是满足约束条件的点），则

                          

                                         

                                         

记原始问题的解为。则对和，。

看到这里可能会有人想，不对啊，我们是搞出来一个“对偶函数”，但是给出的是原始问题的下界啊，也就是说原始问题的解我们还没找到呀。下面就来看看怎么利用对偶函数解原始问题。

• 利用对偶函数解原始问题

既然对偶函数给出了原始问题的下界，且这个下界取决于和的值。那么问题来了：基于对偶函数能得到的最好的下界是什么呢？从而引出优化问题：

                                                                             

                                                                             

这就是原始问题的对偶问题。和称为“对偶变量”。无论原始问题凸性如何，对偶问题始终是凸优化问题。

因为，所以，那么当所有，则“对偶问题”的解也就成了原始问题的解。这就引出了下面的KKT条件。

 

KKT条件

对偶性：

弱对偶性：        强对偶性：

想要成立，

                                                                    

                                                       

                                                        

                                                        

第一个不等号：为极小值，第二个不等号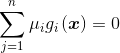：，再加上之前的一些条件，则构成了KKT条件：

                     

                      

                                           

                      

                      

具体的理解看最后的参考博客，讲的很详细。        

             

为什么要用对偶问题呢？

从上面的分析我们可能感觉，对偶问题只是从另一个角度或者是按另一种顺序解决了原始问题。而且强对偶性的成立建立在满足Slater条件。即原始问题为凸优化问题，和为凸函数，为仿射函数(即由一阶多项式构成的函数，f(x)=Ax + b, A是矩阵，x，b是向量)，且其可行域至少有一点使不等式约束严格成立，则此时强对偶性成立。

首先别忘记我们要解决的是SVM中划分超平面的问题。一方面，第一本分确定SVM基本型本身就是一个凸二次规划(convex quadratic programming)，满足Slater条件，即我们可以通过对偶问题求出原始问题的解。另一方面，可以引出核技巧(kernel trick)。

 

SVM中的对偶问题

SVM中的限制条件为：引入拉格朗日乘子，问题的拉格朗日函数写为：

                                            

 对和求偏导为零得：

                                                            

                                                         

带入拉格朗日函数，即可将中的和消去，再考虑约束（即极大极小问题），则得到SVM基本型的对偶问题：

                                                   

                                                   

                                                          

解出后，求出和即可得到模型。

                                                   

需要满足KKT条件：

                                               

从以上的推导我们可以看出：

1）时，对毫无贡献；时，样本必须满足，则该样本位于最大边界上，是一个支持向量。

2）由SVM的对偶问题我们可以看出目标函数只关心乘积的结果，并没有必要每个特征取值都需要知道，这就引出了核技巧(Kernel trick)。在后面的博客中会具体讨论。

 

参考博客：

拉格朗日乘子法与KKT条件：https://blog.csdn.net/weixin_41500849/article/details/80493712

对偶问题：https://blog.csdn.net/fkyyly/article/details/86488582