预测Titanic号上的乘客生存概率_04_分类模型评估和验证(ROC-AUC-KS)

运行环境 jupyter notebook

import numpy as np
import pandas as pd
from sklearn.model_selection import learning_curve   #学习曲线
from sklearn.model_selection import validation_curve #验证曲线
from sklearn.model_selection import train_test_split #拆分数据集
from sklearn.model_selection import cross_val_score  #K折交叉验证

from sklearn import metrics
from sklearn.metrics import confusion_matrix         #误分类矩阵
from sklearn.metrics import precision_score          #准确率
from sklearn.metrics import recall_score             #召回率
from sklearn.metrics import f1_score                 #F1分数
from sklearn.metrics import accuracy_score           #正确率 

test=%run "./预测Titanic号上的乘客生存概率_03_优化训练集.ipynb"

1.通过学习曲线—偏差和方差（样本数与准确率）

数据感知

train_X.head() 
train_y.head() 

svc=SVC()
lr=LogisticRegression()
train_sizes,train_scores,
test_scores=learning_curve(estimator=svc,  #分类模型
                           X=train_X,
                           y=train_y,
                           train_sizes=np.linspace(0.1,1.0,10),  #10%到100%的10个点
                           cv=5,           #K折交叉验证的K值
                           n_jobs=1)  
#查看训练结果                           
train_sizes            #样本数量
train_scores           #训练集准确度
test_scores            #验证集准确度 

绘制 学习曲线诊断偏差和方差图

#计算训练集和测试集准确率的均值和标准差
train_mean=np.mean(train_scores,axis=1)
train_std=np.std(train_scores,axis=1)
test_mean=np.mean(test_scores,axis=1)
test_std=np.std(test_scores,axis=1) 

#对训练集的准确率作图
plt.plot(train_sizes,train_mean,
        color='b',marker='o',
        markersize=5,label='training accuracy')

#对训练集的准确率的可信范围（上下限）作图：上限：train_mean+train_std，下限：train_mean-train_std
plt.fill_between(train_sizes,
                train_mean+train_std,
                train_mean-train_std,
                alpha=0.15,color='b')

#对测试集的准确率作图
plt.plot(train_sizes,test_mean,
        color='g',linestyle='-',
        marker='s',markersize=5,
        label='validation accuracy')

#对测试集的准确率的可信范围（上下限）作图：上限：test_mean+test_std，下限：test_mean-test_std
plt.fill_between(train_sizes,
                test_mean+test_std,
                test_mean-test_std,
                alpha=0.15,color='g')

plt.grid()
plt.xlabel('Number of training samples')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.ylim([0.6,1])
plt.tight_layout()
plt.show()      #图1

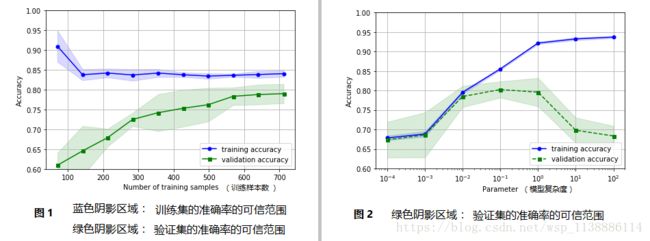
2.通过验证曲线—过拟合和欠拟合 （模型复杂度与准确率）

#模型复杂度的参数
param_range=[0.0001,0.001,0.01,0.1,1.0,10.0,100.0]
train_scores,test_scores=validation_curve(
                estimator=svc,  #lr
                X=train_X,
                y=train_y,
                param_name='gamma',  #C
                param_range=param_range,
                cv=10) 

#对训练集的准确率作图
plt.plot(param_range,train_mean,
        color='b',marker='o',
        markersize=5,label='training accuracy')

#对训练集的准确率的可信范围（上下限）作图：上限：train_mean+train_std，下限：train_mean-train_std
plt.fill_between(param_range,
                train_mean+train_std,
                train_mean-train_std,
                alpha=0.15,color='b')

#对测试集的准确率作图
plt.plot(param_range,test_mean,
        color='g',linestyle='--',
        marker='s',markersize=5,
        label='validation accuracy')

#对测试集的准确率的可信范围（上下限）作图：上限：test_mean+test_std，下限：test_mean-test_std
plt.fill_between(param_range,
                test_mean+test_std,
                test_mean-test_std,
                alpha=0.15,color='g')

plt.grid()
plt.xscale('log')
plt.xlabel('Parameter')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.ylim([0.6,1])
plt.tight_layout()
plt.show()            #结果如上图2

3.模型评估指标之准确率和召回率（混淆矩阵）

test=%run "./预测Titanic号上的乘客生存概率_03_优化训练集.ipynb"

#误分类矩阵
y_test_pred=lr.predict(X_test)
cnf_matrix=metrics.confusion_matrix(y_test,y_test_pred)
cnf_matrix 

#更直观一点的展现误分类矩阵
def show_confusion_matrix(cnf_matrix,class_labels):
    plt.matshow(cnf_matrix,cmap=plt.cm.YlGn,alpha=0.7)
    ax=plt.gca()
    ax.set_xlabel('Predicted Label',fontsize=16)
    ax.set_xticks(range(0,len(class_labels)))
    ax.set_xticklabels(class_labels,rotation=45)
    ax.set_ylabel('Actual Label',fontsize=16,rotation=90)
    ax.set_yticks(range(0,len(class_labels)))
    ax.set_yticklabels(class_labels)
    ax.xaxis.set_label_position('top')
    ax.xaxis.tick_top()
    
    for row in range(len(cnf_matrix)):
        for col in range(len(cnf_matrix[row])):
            ax.text(col,row,cnf_matrix[row][col],va='center',ha='center',fontsize=16)
class_labels=[0,1]
show_confusion_matrix(cnf_matrix,class_labels) 

metrics.precision_score(y_test,y_test_pred) 
metrics.recall_score(y_test,y_test_pred) 
metrics.f1_score(y_test,y_test_pred)
metrics.accuracy_score(y_test,y_test_pred)

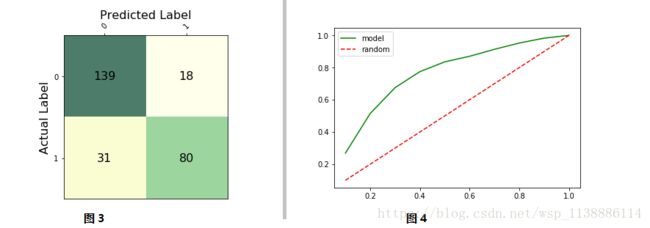
4.模型评估指标之收益曲线

def GainTable(y_true_int,y_pred_prob):                        #y_true_int真实值：正例为1，负例为0
    data=pd.DataFrame({'y_true':y_true_int,'prob':y_pred_prob})
    data['prob']=1-data['prob']
    #计算十分位数并分组
    data['percentile_gp']=pd.qcut(data['prob'],q=10,labels=range(10))
    deciles=data.groupby('percentile_gp',sort=True) 
    
    
    def total_count(x):return len(x)                          #定义函数计算实例总数

    def pos_count(x):return np.sum(x)                         #定义函数计算正例数

    def pos_rate(x):return np.sum(x)/float(len(x))            #定义函数计算正例率
    out=deciles['y_true'].agg([total_count,pos_count,pos_rate])
    out['neg_count']=out['total_count']-out['pos_count']      #计算负例数
    out['pos_cumsum']=out['pos_count'].cumsum()               #计算累计正例数
    total_sum=out['pos_cumsum'][-1]
    out['pos_cover_rate']=out['pos_cumsum']/float(total_sum)  #计算正例覆盖率
    out['percentile']=(out.index.astype(int)+1)/10.0
    return out[['percentile','total_count','pos_count','neg_count','pos_rate','pos_cover_rate']] 

y_train_prob=lr.predict_proba(X_train)
y_pred_prob=y_train_prob[:,1]           #正例率
y_train=list(y_train)
y_pred_prob[:10]                        #正例概率 
y_train[:10]                            #真实标签 

gaintable=GainTable(y_train,y_pred_prob)
gaintable 

def plotGainChart(GainTable):
    plt.plot(GainTable['percentile'],GainTable['pos_cover_rate'],'g-')
    plt.plot(GainTable['percentile'],GainTable['percentile'],'r--')
    plt.legend(['model','random'])
    plt.show()       #图 4
plotGainChart(gaintable)

5.模型评估指标之ROC与AUC

y_train_prob=lr.predict_proba(X_train)
y_pred_prob=y_train_prob[:,1]                             #正例率 
fpr,tpr,thresholds=metrics.roc_curve(y_train,y_pred_prob) #计算ROC曲线
auc=metrics.auc(fpr,tpr)                                  #计算AUC 

#绘制ROC曲线
plt.plot(fpr,tpr,lw=2,label='ROC curve (area={:.2f})'.format(auc))
plt.plot([0,1],[0,1],'r--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc='lower right')
plt.show()       #图 5

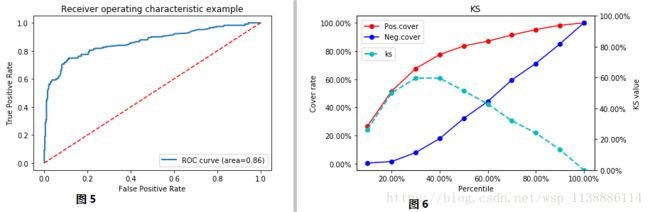
6.模型评估指标之KS值

fig,ax1=plt.subplots()
#主坐标轴上绘制覆盖率曲线
ax1.plot(gaintable['percentile']*100,gaintable['pos_cover_rate']*100,'ro-',label='Pos.cover')
ax1.plot(gaintable['percentile']*100,gaintable['neg_cover_rate']*100,'bo-',label='Neg.cover')

ax2=ax1.twinx()         #建立次坐标轴 

#次坐标轴上绘制KS曲线
ax2.plot(gaintable['percentile']*100,gaintable['ks']*100,'co--',lw=2,label='ks') 

#设置坐标轴格式
ticks=mtick.FormatStrFormatter('%.2f%%')
ax1.xaxis.set_major_formatter(ticks)
ax1.yaxis.set_major_formatter(ticks)
ax2.yaxis.set_major_formatter(ticks) 

#坐标轴标题
ax1.set_xlabel('Percentile')
ax1.set_ylabel('Cover rate')
ax2.set_ylabel('KS value') 

#图例
ax1.legend(loc=(0.02,0.82))
ax2.legend(loc=(0.02,0.71))
ax2.set_ylim(0,100)           #设置次坐标轴范围
plt.title('KS')               #图片标题
plt.show()                    #图 6