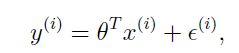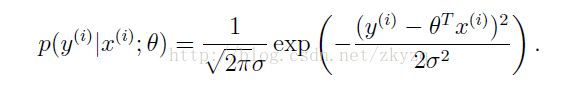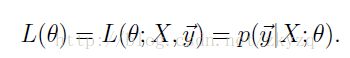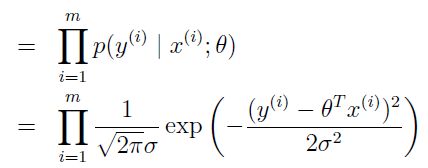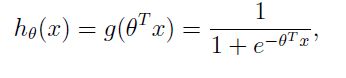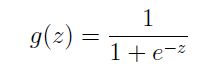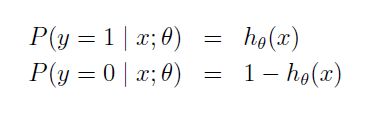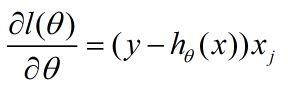机器学习--欠拟合与过拟合
这节课虽然公开课上的标题是欠拟合与过拟合,除了简单讲了一下这两者的概念,实际上Andrew Ng从最原始的线性回归模型展开了一系列拓展,内容包括最小二乘法的概率解释,局部加权线性回归,逻辑回归,另外还简单介绍了一下感知器学习算法。
一、欠拟合与过拟合
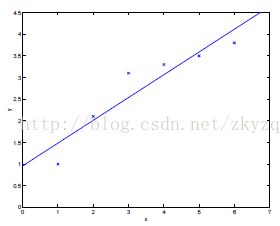
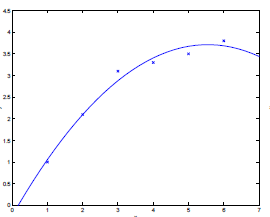
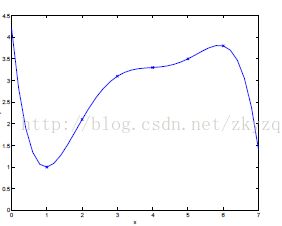
在机器学习中表现不佳的原因不是过拟合就是欠拟合,欠拟合会对训练数据和测试数据都表现不佳,而过拟合对训练数据表现很好,对于测试数据就不尽人意了。可以从下面三幅图理解一下,
(1)欠拟合 (2)中间情况 (3)过拟合
简单来说,欠拟合是因为模型拟合的够好,对于细节把握的还不够完善。而过拟合则太过于注重训练数据的细节,甚至将一些噪声错误的当成特征,可以说类似于训练数据的散点图(比如最右中的图像,六组训练数据我们用了一个五次模型去拟合)。
二、最小二乘法的概率解释
这里我们首先给出几个假设,在这些假设下最小二乘回归是一个非常自然的算法。
1.假设我们学习模型的输出与特征输入有一个这样的关系:
![]() 是这个模型的误差项,可能的来源有我们没有考虑进去的特征量,或者一些随机的,不可控的会影响房价的因素,且这些因素是分布是符合IDD(独立同分布)。概率中的中心极限定理表明这些随机因素的综合作用可以用高斯分布来表示(此处我的粗略理解是,所有的随机因素都起作用的点肯定很少,都不起作用的点也很少,这就类似与正太分布中间高,两头低的特点类似),即
是这个模型的误差项,可能的来源有我们没有考虑进去的特征量,或者一些随机的,不可控的会影响房价的因素,且这些因素是分布是符合IDD(独立同分布)。概率中的中心极限定理表明这些随机因素的综合作用可以用高斯分布来表示(此处我的粗略理解是,所有的随机因素都起作用的点肯定很少,都不起作用的点也很少,这就类似与正太分布中间高,两头低的特点类似),即
这就表明y的分布满足:
其中theta是最小二乘拟合的最佳参数,不是随机变量,而x(i)是则是正态分布的参数。
将上面的结果写成矩阵向量形式:
再根据极大似然定律,最好的参数theta使得![]() 最大,所以我们要极大化
最大,所以我们要极大化![]() 。
。
我们可以看到,如果要极大化上式,即要minimize ,这和我们前面线性回归中代价函数无缝对接,简直是完美。这就说明,在一系列合理的假设和概率条件下,最小二乘法(即残差二范数最小)是自然而然的选择。
,这和我们前面线性回归中代价函数无缝对接,简直是完美。这就说明,在一系列合理的假设和概率条件下,最小二乘法(即残差二范数最小)是自然而然的选择。
三、局部加权线性回归(Locally weighted linear regression)
LWR也被称为是第一个无参数的学习算法的例子,之所以说它无参数,意思是它的参数不固定,对于不同的特征点,它有不同的参数,在一定程度上弥补了线性回归可能造成的欠拟合。算法描述为:
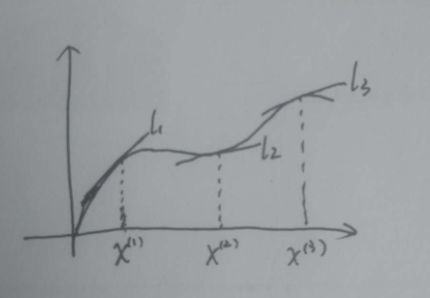
其中 表示的是权重,从这个表达式我们可以得出结论:对于某一个特定特征点x,只有和x距离近的样本点才会被利用,距离x较远的点,由于w(i)较小,我们可以不用考虑。我花了个简单的图试图说明的更清楚一点:
表示的是权重,从这个表达式我们可以得出结论:对于某一个特定特征点x,只有和x距离近的样本点才会被利用,距离x较远的点,由于w(i)较小,我们可以不用考虑。我花了个简单的图试图说明的更清楚一点:
本来应该用曲线才能更好拟合的数据点,现在我们用很多条直线来代替,对于每一个特征点(不管它在不在训练样本里面)我们用一条属于它的直线去代替整体的曲线,所以说这是一种无参数算法,因为其参数随着不同的特征点而变。
四、Logistic 回归
与单纯的线性回归不同,逻辑回归的输出值y只能取0或者1,即只有正样本或者负样本。比如通过病人的一系列特征来确定此病人是否患病,所以逻辑回归用于解决分类问题,且为二分类。
逻辑回归的假设模型选为:
可以看到,当z趋于正无穷时,该函数趋于1,当z趋于负无穷时,该函数趋于0,z取其余值,该函数取值在0和1之间。此处选择其他值在(0,1)之间的函数当然也可以,只是基于某些原因,选择这个函数是自然的(类似于前面最小二乘的概率解释)。下面我们就来看看,如何选取最合适的参数,使得这个模型最为准确。
我们假设:
合并为:
根据前面讲过的极大似然定律,要使得
取到最大的参数即为最合适的模型参数,即对上式求导等于0,Andrew Ng上课时让下课时自己求一下导数,下面是我求的结果:
看,这是不是和之前我们的线性回归模型得到的导数形式一模一样,我还没想清楚为什么会这样,但是Andrew Ng说以后还会讲到...
到了这里,就可以用上一节的梯度下降法来寻找最优参数啦,迭代过程的更新式子为:
下节课还会讲到另一个更好的迭代算法--牛顿法(虽然我已经看完但是还没时间写= =)
最后,Andrew Ng稍微提了一下感知器学习算法,其实它与逻辑回归的不同在于模型函数的选取不一样,它的模型选取的sigmoid函数为:
这一课的内容到这里就结束了,下节课有牛顿方法以及指数分布族和广义线性模型。感觉我要耍流氓了,并没有实现这些算法的代码= =不过这节课的几个模型都是在线性回归的基础上进行一定改变的,后面寻找最优参数的方法还是梯度下降法或者牛顿法。