《数学建模算法与应用》——学习笔记chapter1. 线性规划
1. 线性规划
1.1 定义与标准形
min x c T x \min\limits_x c^T x xmincTx
s . t . { A x ≤ b A e q ⋅ x = b e q l b ≤ x ≤ u b s.t.\begin{cases} Ax\le b\\ Aeq·x=beq\\ lb\le x\le ub \end{cases} s.t.⎩⎪⎨⎪⎧Ax≤bAeq⋅x=beqlb≤x≤ub
其中, min x c T x \min\limits_x c^T x xmincTx称之为目标函数, s . t . { A x ≤ b A e q ⋅ x = b e q l b ≤ x ≤ u b s.t.\begin{cases} Ax\le b\\ Aeq·x=beq\\ lb\le x\le ub \end{cases} s.t.⎩⎪⎨⎪⎧Ax≤bAeq⋅x=beqlb≤x≤ub为约束条件,s.t.即subject to的缩写。由于上面的目标函数及约束条件均为线性函数,故被称为线性规划问题。
线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是小于号也可以是大于号。为了避免这种形式多样性带来的不便,规定线性规划的标准形式如上。其中 c 和 x 为 n 维列向量, A 、Aeq 为适当维数的矩阵,b、beq 为适当维数的列向量。
可以采用加负号的形式使目标函数求最大问题变求最小问题,约束中的大于号变小于号。
1.2 解的概念与解法
满足约束条件的解,称为线性规划问题的可行解,而使目标函数达到最大或值的可行解叫最优解(可以有多个)。
所有可行解构成的集合称为问题的可行域,记为R。
图解法:就是中学那种给你几个函数画出来求最大值的问题,如下图所示
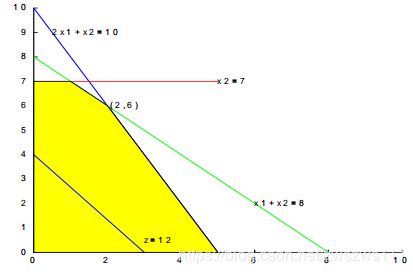
1.3 相关的定义与概念
在一般的n维空间中,满足一线性等式 ∑ i = 1 n a i x i \sum\limits_{i=1}^{n}a_ix_i i=1∑naixi的点集被称为一个超平面,而满足一线性不等式 ∑ i = 1 n a i x i ≤ b \sum\limits_{i=1}^{n}a_ix_i\leq b i=1∑naixi≤b(或 ∑ i = 1 n a i x i ≥ b \sum\limits_{i=1}^{n}a_ix_i\geq b i=1∑naixi≥b)的点集被称为一个半空间(其中 a i a_i ai为一 n n n维行向量, b b b为一实数)。若干个半空间的交集被称为多胞形,有界的多胞形又被称为多面体。易见,线性规划的可行域必为多胞形(为统一起见,空集 Φ \Phi Φ也被视为多胞形)
n n n维空间中的区域 R R R为一凸集,则 ∀ x 1 , x 2 ∈ R \forall x^1,x^2\in R ∀x1,x2∈R及 ∀ λ ∈ ( 0 , 1 ) \forall\lambda\in(0,1) ∀λ∈(0,1)有 λ x 1 + ( 1 − λ x 2 ) ∈ R \lambda x^1+(1-\lambda x^2)\in R λx1+(1−λx2)∈R。
1.4 matlab解法
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
这里 f v a l fval fval返回目标函数的值, L B LB LB和 U B UB UB分别是变量 x x x的下界和上界, x 0 x_0 x0 是 x x x的初始值, O P T I O N S OPTIONS OPTIONS 是控制参数
只要在matlab中输入对应的矩阵调用函数即可求解。
1.5 可转化为线性规划的问题
对于一些看上去不是线性规划的问题,可以通过一些数学变换将其转换为线性规划的标准形。
如对问题 min ∣ x 1 ∣ + ∣ x 2 ∣ + ⋅ ⋅ ⋅ + ∣ x n ∣ \min |x_1|+|x_2|+···+|x_n| min∣x1∣+∣x2∣+⋅⋅⋅+∣xn∣ , s . t . A x ≤ b s.t.Ax\leq b s.t.Ax≤b
只要令 x i = u i − v i . ∣ x i ∣ = ∣ u i ∣ + ∣ v i ∣ x_i=u_i-v_i.|x_i|=|u_i|+|v_i| xi=ui−vi.∣xi∣=∣ui∣+∣vi∣,即可将问题转化为
min ∑ i = 1 n ∣ u i ∣ + ∣ v i ∣ \min\sum\limits_{i=1}^{n}|u_i|+|v_i| mini=1∑n∣ui∣+∣vi∣
s . t . { A ( u − v ) ≤ b u , v ≥ 0 s.t.\begin{cases} A(u-v)\leq b\\ u,v\geq 0 \end{cases} s.t.{A(u−v)≤bu,v≥0
2. 产销平衡(运输问题)
例:某商品有 m m m个产地、 n n n个销地,各产地的产量分别为 a 1 . . . a m a_1...a_m a1...am,各销地的需求量分别为 b 1 . . . b n b_1...b_n b1...bn。若该商品由 i i i产地运到 j j j销地的单位运价为 c i j c_{ij} cij,问应该如何调运才能使总运费省?
解:引入变量 x i j x_{ij} xij ,其取值为由 i i i产地运往 j j j销地的该商品数量,数学模型为
min ∑ i = 1 m ∑ j = 1 n c i j x i j \min\sum\limits_{i=1}^{m}\sum\limits_{j=1}^nc_{ij}x_{ij} mini=1∑mj=1∑ncijxij
s . t . { ∑ j = 1 n x i j = a i , i = 1... m ∑ i = 1 m x i j = b j , b j = 1... n x i j ≥ 0 s.t. \begin{cases} \sum\limits_{j=1}^n x_{ij}=a_i, i=1...m\\ \sum\limits_{i=1}^m x_{ij}=b_j,b_j=1...n\\ x_{ij}\geq 0 \end{cases} s.t.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧j=1∑nxij=ai,i=1...mi=1∑mxij=bj,bj=1...nxij≥0
此类问题可用单纯形法求解
3. 指派问题
3.1 指派问题的是数学模型
例:拟分配 n n n人去干 n n n项工作,每人干且仅干一项工作,若分配第 i i i人去干第 j j j项工作,需花费 c i j c_{ij} cij单位时间,问应如何分配工作才能使工人花费的总时间最少?
解:引入变量 x i j x_{ij} xij,若分配 i i i干 j j j工作,则取 x i j = 1 x_{ij}= 1 xij=1,否则取0 。上述指派问题的数学模型为
min ∑ i = 1 n ∑ j = 1 n c i j x i j \min\sum\limits_{i=1}^{n}\sum\limits_{j=1}^nc_{ij}x_{ij} mini=1∑nj=1∑ncijxij
s . t . ∑ j = 1 n x i j = 1 s.t. \sum\limits_{j=1}^nx_{ij}=1 s.t.j=1∑nxij=1
∑ i = 1 n x i j = 1 \sum\limits_{i=1}^nx_{ij}=1 i=1∑nxij=1
x i j ∈ 0 , 1 x_{ij}\in{0,1} xij∈0,1
问题中的变量只能取0或1,是一个0-1规划问题。指派问题是一个特殊的运输问题,其中 m = n , a i = b j = 1 m=n ,a_i = b_j =1 m=n,ai=bj=1。
3.2 求解指派问题的匈牙利算法
如果系数矩阵 C = c i j C=c_{ij} C=cij一行(或一列)中每一元素都加上或减去同一个数,得到一个新矩阵 B = b i j B=b_{ij} B=bij,则以 C C C或 B B B为系数矩阵的指派问题具有相同的最优指派。
对于系数矩阵 C = [ 16 15 19 22 17 21 19 18 24 22 18 17 17 19 22 16 ] C=\begin{bmatrix} 16 & 15&19&22 \\ 17 & 21&19&18\\ 24&22&18&17\\ 17&19&22&16 \end{bmatrix} C=⎣⎢⎢⎡16172417152122191919182222181716⎦⎥⎥⎤,首先对于每行(每列)减去改行(列)的最小元素,得到新的矩阵 B = [ 1 0 3 7 0 4 1 1 7 5 0 0 1 3 5 0 ] B=\begin{bmatrix} 1 & 0&3&7 \\ 0 & 4&1&1\\ 7&5&0&0\\ 1&3&5&0 \end{bmatrix} B=⎣⎢⎢⎡1071045331057100⎦⎥⎥⎤,对该矩阵,从含0元素最少的行或列开始,圈出一个0元素,划去该行(列)的其它0元素,依此类推。若能圈出n个(矩阵维度),则得最优解 ( 1 2 3 4 2 1 3 4 ) \begin{pmatrix} 1 & 2&3&4 \\ 2 & 1&3&4 \end{pmatrix} (12213344),其每列组成一个索引对应B中的0
元素位置。
对于能够找出的0元素小于n(矩阵维度)的情况,依然能做等价变换:
(1) 对未选出 0 元素的行打∨ ;
(2) 对∨ 行中 0 元素所在列打∨ ;
(3) 对∨ 列中选中的 0 元素所在行打∨ ;
重复(2)、(3)直到无法再打∨ 为止。
可以证明,若用直线划没有打 ∨ 的行与打 ∨ 的列,就得到了能够覆盖住矩阵中所有零元素的最少条数的直线集合,找出未覆盖的元素中的最小者,令 ∨ 行元素减去此数,∨ 列元素加上此数,则原先选中的 0 元素不变,而未覆盖元素中至少有一个已转变为 0,且新矩阵的指派问题与原问题也等价。
4. 对偶问题与灵敏度分析
4.1 原问题与对偶问题
考虑一般的线性规划问题:
max c T x , s . t . A x ≤ b , x ≥ 0 \max c^Tx ,s.t.Ax\leq b,x\geq0 maxcTx,s.t.Ax≤b,x≥0称为原问题
min b T y , s . t . A T y ≥ c , y ≥ 0 \min b^Ty,s.t.A^Ty\geq c,y\geq0 minbTy,s.t.ATy≥c,y≥0称为原问题的对偶问题。
4.2 基本性质
- 对称性:对偶问题的对偶是原问题。
- 弱对偶性:若 x 是原问题的可行解, y 是对偶问题的可行解。则存在 c T x ˉ ≤ b T y ˉ c^T\bar x\leq b^T\bar y cTxˉ≤bTyˉ。
- 无界性:若原问题(对偶问题)为无界解,则其对偶问题(原问题)无可行解。
- 可行解是最优解时的性质:设 x ^ \hat x x^是原问题的可行解, y ^ \hat y y^是对偶问题的可行解,当 c T x ^ = b T y ^ c^T\hat x = b^T\hat y cTx^=bTy^时,是最优解。
- 对偶定理:若原问题有最优解,那么对偶问题也有最优解;且目标函数值相同。
- 互补松弛性:若 x ^ \hat x x^, y ^ \hat y y^分别是原问题和对偶问题的最优解,则 y ^ T ( A x ^ − b ) = 0 \hat y^T(A\hat x-b)=0 y^T(Ax^−b)=0, x ^ T ( A T y ^ − c ) = 0 \hat x^T(A^T\hat y-c)=0 x^T(ATy^−c)=0
4.3 灵敏度分析
线性规划中系数矩阵往往是预测值或估计值当这些系数有一个或几个发生变化时,已求得的线性规划问题的最优解会有什么变化;或者这些系数在什么范围内变化时,线性规划问题的最优解或最优基不变。这就是灵敏度分析的内容。
参考文献
convex optimization
匈牙利算法