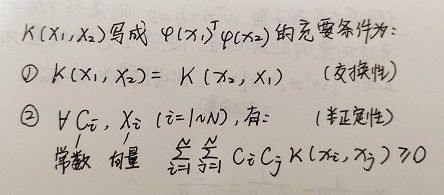机器学习SVM详细推导过程

手写的公式实在很难搬上来，就直接照片吧…

1.线性可分

首先先普及SVM的一些基本知识：
在这之前，假设读者们对线性分类模型和向量矩阵求导有大概的了解。

给定训练样本集D={($x_1,y_1$),($x_2,y_2$),…,($x_m,y_m$)}，$y_i\in (-1,+1)$ ，线性分类器基于训练样本D 在二维空间中找到一个超平面来分开二类样本。当然，这样的超平面有很多。

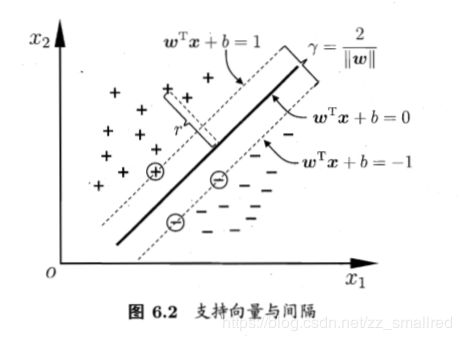
但我们可以直观的感觉到，中间这条颜色最深的线代表的超平面抗“扰动”性最好。这个超平面离直线两边的数据的间隔最大，对训练集的数据的局限性或噪声有最大的“容忍”能力。这个超平面的描述为：

其中，w=($w_1;w_2;...;w_d$)为法向量，决定了超平面的方向；b为位移项，决定了超平面与原点之间的距离。显然，划分超平面可被法向量w和位移b确定。
（法向量w和变量x均为n行1列矩阵，两个矩阵相乘需要进行转置操作，所以法向量w进行了转置。）

根据点到直线的距离公式，可以推导得出样本空间中任一点x到超平面（w,b）的距离公式：

每个训练样本都必须满足的条件：

支持向量：距离超平面最近的这几个训练样本点使上式的等号成立，则这些点被称为“支持向量”（support vector）。

为求得两个异类支持向量到超平面的距离之和，我们首先需要知道：

所以两个异类支持向量到超平面的距离之和（也称“最大间隔”）为：

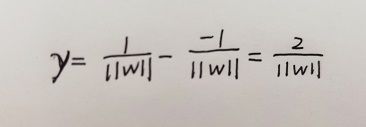
至此，我们可以根据现有条件，找到具有“最大间隔”的划分超平面：

为了最大化间隔，我们需要转化求最大值为求最小值。（$\frac{1}{2}$和平方为方便求导，不影响结果。）

转化后的问题是一个凸优化问题中的二次规划问题。

——————————————————————

2.线性不可分

2.1 松弛变量

线性不可分情况下，优化问题将写为：

这里我们引入了一个新的变量，松弛变量（slack variables），目的是允许某些样本点的函数间隔小于1，即在最大间隔区间里面，或者函数间隔是负数，即样本点在对方的区域中。为什么我们要这样做呢，因为在实际情况中，会存在一些离群点（有可能是噪声），这些离群点的出现造成最大间隔变小，并且需要对整个模型进行重新调整，可以说是“害群之马”。松弛变量的引入，正是为了解决这个问题。

注意：

• 目标函数后面加上的正则项越大就表示离群点越多，目标函数值越大，而我们要求的是尽可能小的目标函数值。
• 这里的C是离群点的权重，C越大表明离群点对目标函数影响越大，也就是越不希望看到离群点。我们看到，目标函数控制了离群点的数目和程度，使大部分样本点仍然遵守限制条件。
• C是常数，w，b，$\xi$（i=1,2,…,N）为待求变量
• $y_i[w^T{x}_i+b]=1⟺$ $x_i$为支持向量

2.2 核函数

在现实中，原始样本空间内也许并不存在一个能够正确划分两类样本的超平面，所以我们为了解决这类问题，我们可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

将上面这句话翻译过来，就是我们要对向量x进行升维处理，使得样本在更高维的特征空间内线性可分。

由于无法直观计算出进行升维处理后的值，因此使用核函数进行表述：

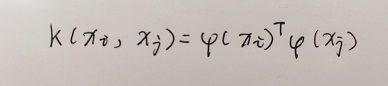
（核技巧：$x_i$与$x_j$在特征空间的内积等于它们在原始样本空间中通过核函数k(. , .)计算的结果。有了这样的函数，我们就不必直接去计算高维甚至无穷维特征空间中的内积。）

但要使用核函数进行计算，需要满足一定的条件：

2.3 对偶问题推导

2.3.1 定义

你看到这里可能都会一头雾水，我是谁，我在干什么，前面我看的东西到底有什么用？别着急，前面的内容都是为对偶问题求解服务的。没有前面的铺垫，对偶问题别想解决。

明确下目标，我们的目标是求取一定条件下的w和b。

首先我们先将原问题和对偶问题列出来。

对原问题使用拉格朗日乘子法可得到其“对偶问题”。具体来说，就是对原问题的每条约束添加拉格朗日乘子${\alpha }_i\ge$ 0。
（拉格朗日乘子法用于求函数f在g约束下的极值问题）

对偶问题列出来后，可以定义：

这里最大化的意思是，在限定了$\alpha$和$\beta$的情况下，遍历所有的w，求L的最小值。每确定一个$\alpha$和$\beta$，就会有一个最小值，在这些最小值中找出它们中的最大值。

注意，这里有两个定理。
定理1：

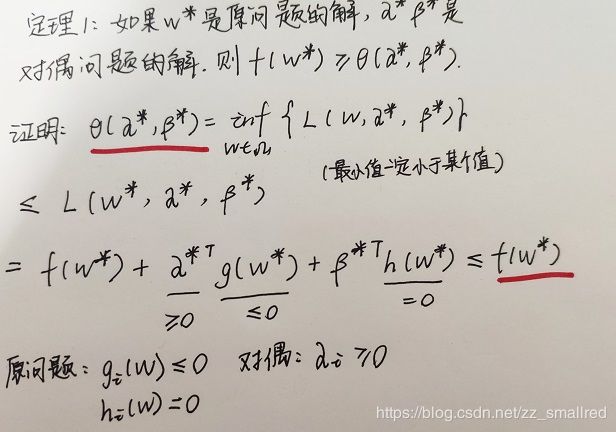
定理2：


到此为止，我们结束了对定理的推导。接下来开始进行对偶问题的推导

2.3.2 推导

首先我们要做的事情是对目标函数和限制条件进行修改。为什么要进行修改呢？因为对偶问题的限制条件与原问题的限制条件有所偏差，所以需要更改。

由于原问题的限制条件为

对偶问题的限制条件要与原问题保持一致，即要将条件②的≥改成≤，即修改成：

（符号变更是松弛变量$\xi$的取值范围改变导致的）

由于原问题的待求变量w对应过来对偶问题的待求变量分别为（w，${\xi }_i$，b），所以问题变为：

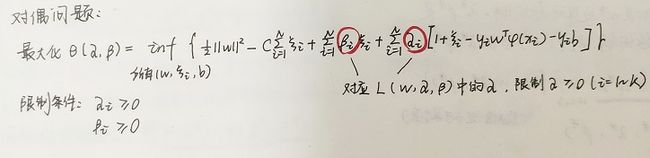
分别对三个变量求偏导，可得：

将所得结果代入公式中，可得：


到了这里，我们已经将问题转化为求极值的问题了。使用SMO算法继续进行计算，这里由于篇幅原因就不介绍了。

2.4 求得w和b

由上面的求导可知w：

使用kkt条件来求取b：


回到测试流程，我们得到：

根据上图所得和b的值相加，根据值和0的大小比较，可以对样本空间内的样本进行判断、分类。

3. 算法流程

——————
终于是整理出来SVM了。累。