强对偶性、弱对偶性以及KKT条件的证明(对偶问题的几何证明)
目录
- 1.原问题
- 2.对偶问题
- 2.1弱对偶性的一般证明
- 2.2弱对偶性的几何证明
- 2.3强对偶性的几何表示以及条件
- 2.4 slater condition
- 3.KKT条件的证明
- 3.1可行条件
- 3.2互补松弛条件
- 3.3偏导为0条件
1.原问题
首先给出问题的一般形式:
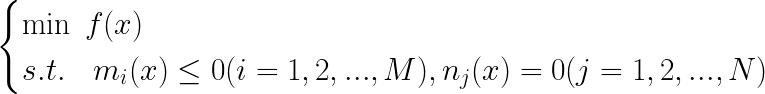
上式表明我们一共有M+N个约束条件,对于不是求最小值或者约束条件大于等于0的情况,我们添加一个负号就可以变成上面这种形式。
上述问题我们一般称之为带约束的原问题。
利用拉格朗日乘子法,我们构造一个新的函数以及约束条件如下:

其中: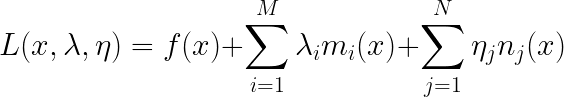
我们称上面的问题为无约束的原问题(对x不再有约束)。上述L是拉格朗日乘子法的基本形式,这个就不再证明。
2.对偶问题
对于无约束的原问题,我们先直接给出它的对偶问题形式(其实就是简单交换min和max):
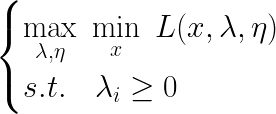
上述问题我们称之为原问题的对偶问题。
2.1弱对偶性的一般证明
所谓弱对偶性,指的是:
![]()
在再谈SVM(hard-margin和soft-margin详细推导、KKT条件、核技巧)中,我们大致口头证明了弱对偶性的成立,即“凤尾”>=“鸡头”。何谓“凤尾”?我先选出最强的一批人( max f \max f maxf),然后组成实验班,实验班倒数第一就是 min max f \min \ \max f min maxf;何谓“鸡头”?我先选出最弱的一批人( min f \min f minf),然后在这批比较弱的人当中选出最强的那个人,也即是 max min f \max \ \min f max minf,那么“鸡头”与“凤尾”孰强孰弱,是显而易见的。
现在我们利用数学推导来大致证明一下弱对偶性。
对于 L ( x , λ , η ) L(x,\lambda,\eta) L(x,λ,η)这个函数,我们知道下面这个不等式一定成立:
![]()
上面这个不等式很好理解,中间 L ( x , λ , η ) L(x,\lambda,\eta) L(x,λ,η)我们可以理解为L的值域,值域里面的任何一个数,必然是大于等于它的最小值,小于等于它的最大值。其实这一步已经证明出弱对偶性了,不过为了更容易理解,我们可以进一步说明。
上述不等式最左边的表达式最后是关于 λ , η \lambda,\eta λ,η的一个函数,而最右边是一个关于 x x x的函数,因此我们又令:
![]()
因此我们有:
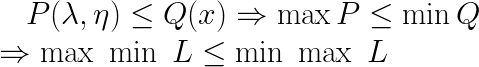
证毕。
2.2弱对偶性的几何证明
为了使问题简化,同时方便证明,我们去掉原问题中等式的约束条件,同时不等式约束条件只保留一个,即原问题变成:

那么拉格朗日函数就变成:
![]()
我们又令:
![]()
即 p ∗ p^* p∗是原问题的最优解, d ∗ d^* d∗是对偶问题的最优解。证明弱对偶性实际上就是证明 d ∗ ≤ p ∗ d^*\leq p^* d∗≤p∗。
我们令区域G的表达形式为:
![]()
D是原问题的定义域,G表示一个个点的集合,点的横坐标是约束条件 u = m 1 ( x ) u=m_{1}(x) u=m1(x),纵坐标是原函数 t = f ( x ) t=f(x) t=f(x)。
有了上述集合G的定义之后,我们就可以对 p ∗ , d ∗ p^*,d^* p∗,d∗进行变式。
首先对 p ∗ p^* p∗进行变式:
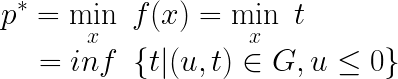
因为 t = f ( x ) t=f(x) t=f(x),所以 p ∗ p^* p∗实际上就是t的最小值,反映到集合G中去就是指一个点的纵坐标,这个点要满足两个条件:一是肯定要在G中,二是 m 1 ( x ) ≤ 0 m_{1}(x)\leq0 m1(x)≤0也就是该点的横坐标小于等于0。
如下图所示:
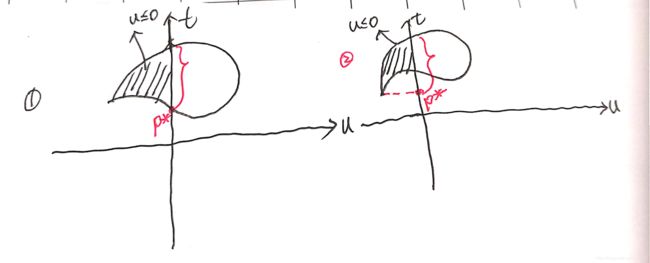
我们对 u ≤ 0 u\leq0 u≤0那部分,也就是图中阴影部分上的每个点,找到一个最低的点,它的纵坐标就是 p ∗ p^* p∗。
接着对 d ∗ d^* d∗进行变形:
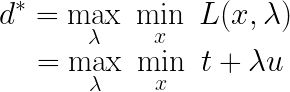
上述 t + λ u t+\lambda u t+λu的来源为:
![]()
对变形后 d ∗ d^* d∗我们令:

我们先找到 g ( λ ) g(\lambda) g(λ)在图中的位置:我们知道 t + λ u t+\lambda u t+λu实际上也是一个值,我们不妨令 t + λ u = k t+\lambda u=k t+λu=k,该式表示一条斜率为 − λ -\lambda −λ并过(0,k)的直线,我们要找的是 t + λ u t+\lambda u t+λu的最小值,实际上就是k的最小值,实际上就是该直线与纵轴交点的最小值。而在求 min x t + λ u \min \limits_{x}\ t+\lambda u xmin t+λu的最小值时, λ \lambda λ是固定的,因此斜率 − λ -\lambda −λ也是固定的:
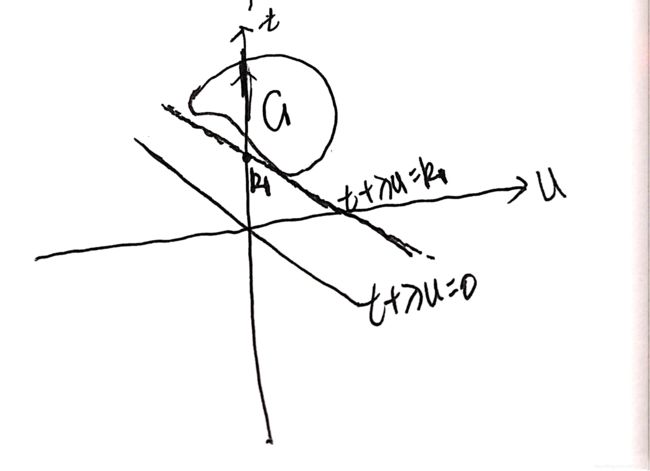
我们保持斜率不变移动直线,不断往上移动,则该直线与纵轴交点的纵坐标k也不断增大,因为限制条件还有一个就是 ( u , t ) ∈ G (u,t)\in G (u,t)∈G,因此该直线必须经过区域G,我们一直往上移动,直到直线第一次与G相交,记下相应的k值为 k 1 k_{1} k1,再继续往上也都满足条件,知道该直线与G不再相交,但是现在我们求得是最小值,那么最小值其实就是 k 1 k_{1} k1,即 g ( λ ) g(\lambda) g(λ)就等于 k 1 k_{1} k1。
进一步,我们要求:
![]()
这里要重点注意:上一步我们求得了 g ( λ ) g(\lambda) g(λ)就等于 k 1 k_{1} k1,但是这种情况只是一种情况,在上一步求 g ( λ ) g(\lambda) g(λ)时,我们假若改变斜率 − λ -\lambda −λ,那么 k 1 k_{1} k1的值是会变的,如下所示:
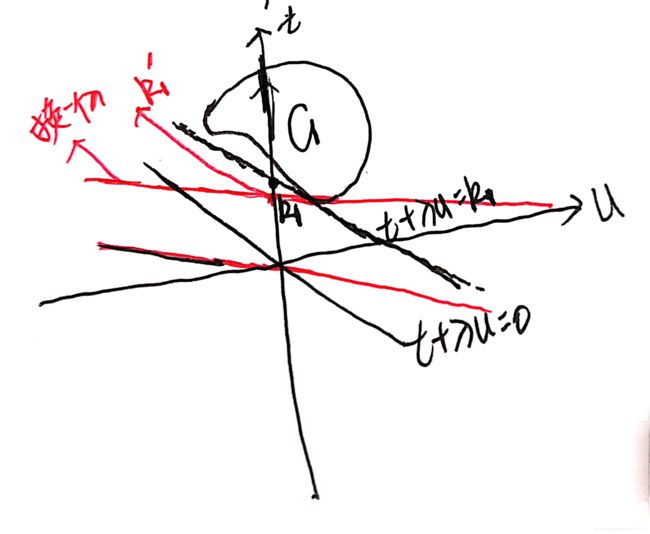
我们换一个 λ \lambda λ固定时, g ( λ ) g(\lambda) g(λ)也就是 k 1 k_{1} k1自然也就在变。
第二步要干的其实就是让我们求这个 g ( λ ) g(\lambda) g(λ)的最大值。那什么时候是最大的?实际上就是以G的最低点为轴,我们旋转直线,直到与左上方最低点相交时, g ( λ ) g(\lambda) g(λ)是最大的。如下所示:
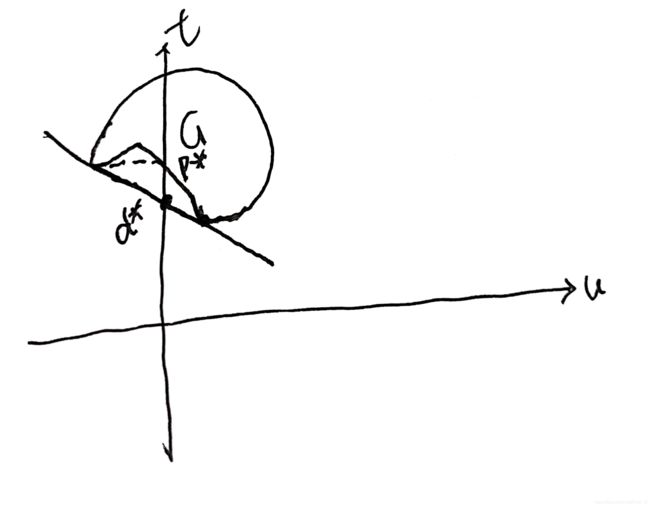
可能很多人就有疑问了:我为什么不可以让斜率继续增大?让直线穿过G?这里有疑问的同学不妨回忆一下第一个步骤:

我们在确定 g ( λ ) g(\lambda) g(λ)的时候,第一次相切我们就停止了,而后改变斜率继续相切:如上图所示,假如你继续增大斜率,那么该直线就不跟G的最低点相切了。我们是先推第一步再推第二步,而推第二步的时候肯定必须满足第一步的条件,所以 d ∗ d^* d∗只能是在那个位置。
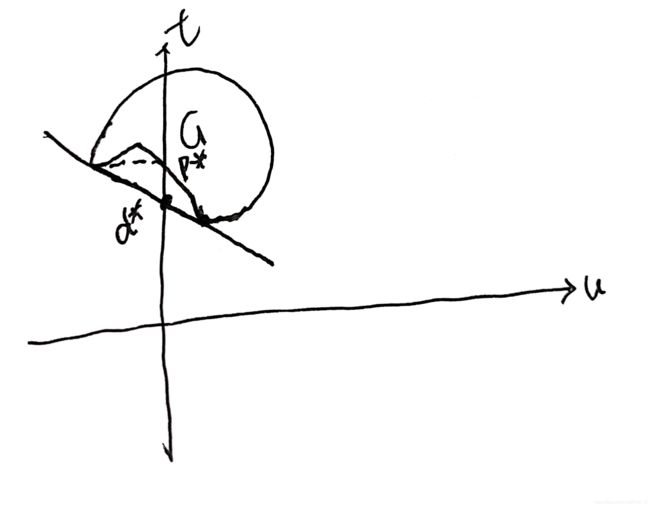
从上图也可以看出来: d ∗ ≤ p ∗ d^*\leq p^* d∗≤p∗,也就是对偶问题的解是小于等于原问题的解的,也即是说满足弱对偶性。因此这里我们进一步证明了弱对偶性。
2.3强对偶性的几何表示以及条件
什么是强对偶性?就是指原问题的解与对偶问题的解是相同的,也即是: d ∗ = p ∗ d^*=p^* d∗=p∗。
画个图:

假设G是一个凸集,那么根据上面找 d ∗ d^* d∗和 p ∗ p^* p∗的思路,我们很容易知道这个时候二者是相等的,也就是满足强对偶关系。
那上面这句话的意思就是说:只要是凸集就一定满足强对偶关系。这句话不是正确的,不是所有的凸集都满足强对偶关系,但是加上slater条件就一定满足。
2.4 slater condition
先直接给出slater条件的定义:对于x的定义域D,如果它存在一个内点(不是边界上的点) x ∗ x^* x∗满足对任意的 m i ( x ) < 0 , i = 1 , 2 , . . . , M m_{i}(x)\lt0,i=1,2,...,M mi(x)<0,i=1,2,...,M,则说明该问题满足slater条件。
对slater条件做两点说明:
- 对于大多数的凸优化问题来说,slater condition都是成立的
- 放松的slater条件:如果约束函数 m i ( x ) , i = 1 , 2 , . . . , M m_{i}(x),i=1,2,...,M mi(x),i=1,2,...,M中有K个是仿射函数,则我们只需要那M-K个约束函数满足第一个条件,我们也说该问题满足slater条件。
- 什么是仿射函数?仿射函数,即最高次数为1的多项式函数。常数项为零的仿射函数称为线性函数。简单来说,就是比较简单的函数。
对第一个条件进一步说明:为什么我们要满足这个条件?第一个条件放在G中的意思就是:G在u<0部分必须有点存在:

假设纵坐标左边没有点,那么在我们寻找 g ( λ ) g(\lambda) g(λ)时,那条直线实际上就会是纵坐标轴。
3.KKT条件的证明
通过上面的推导我们知道了:
![]()
满足强对偶关系之后我们就得到一个结论: d ∗ = p ∗ d^*=p^* d∗=p∗,但是也到此为止了,我们肯定得解出那些未知最优参数(带 * 的变量),KKT条件就是干这件事。
KKT条件有三部分:可行条件、互补松弛条件以及偏导为0条件,我们一个一个推导。
3.1可行条件
所谓可行条件,指的是一开始就满足的一些条件:
![]()
这三个条件肯定得满足,这个没啥可说的,天然满足。
3.2互补松弛条件
我们知道:
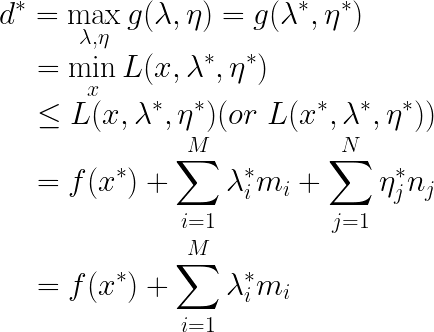
带星号的都是最优解的意思。根据可行条件我们知道: λ i ≥ 0 , m i ≤ 0 \lambda_{i}\geq0,m_{i}\leq0 λi≥0,mi≤0,所以 λ i m i ≤ 0 \lambda_{i}m_{i}\leq0 λimi≤0,所以上面继续变换:
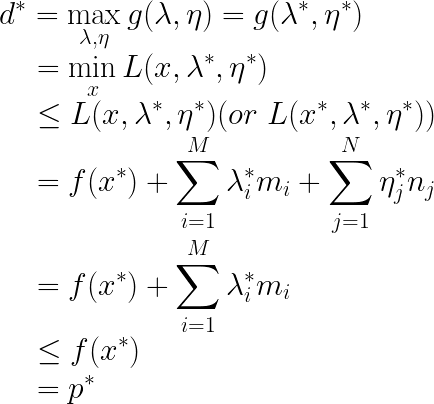
因为最后一步等于第一步,所以中间推导步骤中的 ≤ \leq ≤都应该变成=,倒数第三步等于倒数第二步,所以我们有:

而前面我们又知道 λ i m i ≤ 0 \lambda_{i}m_{i}\leq0 λimi≤0,所以互补松弛条件如下:
![]()
3.3偏导为0条件
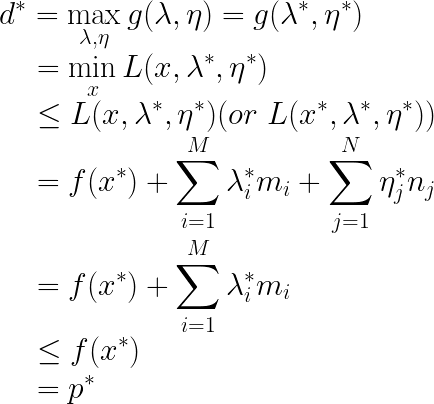
继续看这个推导,第二、三步之间应该用等号连接,即:
![]()
意思就是说L在 x = x ∗ x=x^* x=x∗处有最小值,于是偏导为0条件就出来了:
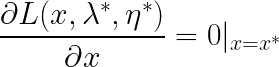
于是KKT条件为:
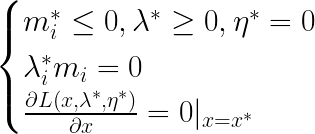
证毕。