关于Karush-Kuhn-Tucker（KKT）条件的几何分析

写在前面的话

Karush-Kuhn-Tucker（简称“KKT”）条件是优化学里解决拉格朗日对偶问题的一种重要思想，被广泛应用在运筹学，凸与非凸优化，机器学习等领域。在这篇博客中我尝试用几何的角度解释拉格朗日对偶问题与对KKT条件的理解。如果想进一步学习凸优化内容，推荐Stanford CS229课程与Stephen Boyd教授的经典教材《Convex Optimization》，都对凸优化的内容进行了非常清晰的讲解。在这篇博客中我会尽量假设读者对凸优化相关内容比较陌生，所以用比较通俗易懂的语言进行描述，在一些有延伸的地方用注解的方式加以说明。如果有理解上有问题或言之不确之处，可以在留言中指正，欢迎一起探讨。

---

凸优化问题

凸优化问题是一类比较特殊的优化问题，在世界上其实只有比较少数的问题可以适用于凸优化来解决，但因为凸优化理论被研究得比较彻底，也被广泛应用在精确方法问题[^footnote]的解决上，所以研究凸问题仍然是非常重要的。关于凸函数的定义与基本性质，本文就不赘述了。

凸优化的定义是求取最小值的目标函数为凸函数的一类优化问题。其中，目标函数为凸函数且定义域为凸集的优化问题称为无约束凸优化问题。目标函数和不等式约束函数均为凸函数，等式约束函数为仿射函数，并且定义域为凸集的优化问题为带约束凸优化问题。我们在这里探讨带约束凸优化问题，具有如下的形式：

minf0(x)s.t.fi(x)≤0,i=1,...,m hi(x)=0,i=1,...,pminf0(x)s.t.fi(x)≤0,i=1,...,m hi(x)=0,i=1,...,p

这里我们定义函数集fi(x)fi(x)是凸函数集，hi(x)hi(x)是仿射函数集。小标s.t.所列举的代表强约束，通常这些约束关系不会出现在传统的机器学习的损失函数中，在机器学习中的目标函数通常不需要具有特定的真实含义，比如目标函数只代表在优化过程中的优化进程的一种抽象的度量方法。但是在凸优化与运筹学中，目标函数往往代表一些实际的意义。我们要寻找的解是最小化fi(x)fi(x)的同时还要满足所有等式约束hi(x)hi(x)与不等式约束fi(x)fi(x)。

一边优化一边带着约束是很困难的。对于等式约束，典型的解决办法有牛顿迭代法： 

[∇2f(x)AA0][Δxnewtonw]=[−∇f(x)0][∇2f(x)AA0][Δxnewtonw]=[−∇f(x)0]
求解迭代 ΔxnewtonΔxnewton 的过程中可行解在同时满足等式约束时逐渐优化了目标函数。对于不等式约束问题可以使用对数障碍法求解，将不等式约束变成对数形式的障碍，将解原问题转变为解如下的问题：

   minf0(x)−(1/t)∑i=1mlog(−fi)s.t.   hi(x)=0,i=1,...,p   minf0(x)−(1/t)∑i=1mlog(−fi)s.t.   hi(x)=0,i=1,...,p

如公式中所揭露的，当解从负方向靠近0时会承受对数障碍带来的惩罚效果。关于牛顿迭代法与对数障碍法有兴趣的同学可以搜索相关教程，在此不再赘述。下面从对偶问题和原始问题两方面分析拉格朗日函数。

---

拉格朗日函数

拉格朗日乘子法，（或称广义拉格朗日函数）与前两种方法的区别在于，前两种优化方法直接将约束条件融合进了目标函数，令约束依然维持强约束的效果。但拉格朗日试图构造一个原问题的对偶问题，将约束从强约束转化为弱约束，使约束关系可以在某些情况下被违反。拉格朗日对偶问题表述为： 

L(x,λ,ν)=f0(x)+∑i=1mλifi(x)+∑i=1pνihi(x)L(x,λ,ν)=f0(x)+∑i=1mλifi(x)+∑i=1pνihi(x)

这种构造看起来确实很奇怪，既然约束都变成可以违反的了，还怎么保证能找到原问题的最优解呢？这就是拉格朗日对偶问题有趣的地方了。在这个对偶问题中，引入了两个标量矢量 λλ 与 νν 用来表示非等式与等式约束在对偶问题中所起的作用大小，他们被称作“对偶变量”。解决拉格朗日问题可以从对偶问题与原始问题两个方面入手，下面将分开介绍。

---

对偶问题

什么是对偶问题？这可以牵扯到认知世界的方法论。比如我们永远无法知道别人眼中的自己是什么样的，有趣的是我们往往不关心自己是否真的好看，而更希望别人认为我们好看，这其实是两个问题（所以美颜相机会如此风靡全球）。如果后者是优化的原问题，那前者就是这个问题的对偶问题。因为我们没办法知道别人眼中的自己是什么样子，所以我们只能通过优化对偶问题（对着镜子打扮）来间接地优化原问题。

回到拉格朗日问题上来，我们假设这些约束可以添加一些任意程度的影响（或“惩罚”）到原问题上，但这些约束到底是怎么影响原问题的呢？因为我们最终的目的是最小化拉格朗日函数，我们需要首先选择一个变量，这里我们选原变量xx，有：

g(λ,ν)=infx∈DL(x,λ,ν)=infx∈D⟮f0(x)+∑i=1mλifi(x)+∑i=1pνihi(x)⟯g(λ,ν)=infx∈DL(x,λ,ν)=infx∈D⟮f0(x)+∑i=1mλifi(x)+∑i=1pνihi(x)⟯

找到了这个最优值之后，对偶问题就变为关于 λλ 和 νν 的函数，所以包含 xx 的函数 f0(x)f0(x) ， fi(x)fi(x) 与 hi(x)hi(x) 则变成了常量。注意定义在仿射函数簇上的下确界(infimum)是凹的[^footnote]，所以我们可以将这个问题转变为求对偶乘子的最大化问题，有： 

 maxg(λ,ν)s.t. λ⪰0 maxg(λ,ν)s.t. λ⪰0

我们可以这样理解，固定了最优解 xx 之后，在优化 λλ 与 νν 的过程中会带来一些违反约束的情况。于是我们可以引入“惩罚”的的概念，让这些约束对违反约束的解进行惩罚。我们在最大化 g(λ,ν)g(λ,ν) 的过程中总可以找到这样的一组合适的 λλ 与 νν ，使这个解对 L(x,λ,ν)L(x,λ,ν) 的惩罚尽可能地大。这一惩罚过程是很有趣的，将在原始问题的部分做进一步阐述。

现在将拉格朗日对偶函数的极大极小问题表示为约束最优问题，即： 

  maxλ,ν g(λ,ν)=maxλ,νminx L(x,λ,ν)s.t.   λi⪰0  maxλ,ν g(λ,ν)=maxλ,νminx L(x,λ,ν)s.t.   λi⪰0

注意此处有约束λi⪰0λi⪰0，这是KKT的一个重要条件稍后会具体谈，假设这个优化问题得到的最优值为对偶最优解，记作d∗d∗.

---

原始问题

这里对拉格朗日问题的原始问题稍作探讨。由上得知拉格朗日函数是三个变量xx, λλ和νν的函数，而原始问题只是关于xx的函数，因此若要寻找拉格朗日函数与原始函数的关系，需要先找到一个中间函数来消除λλ和νν的不确定性。我们假设有关于xx函数： 

j(x)=supλ⪰0,νL(x,λ,ν)=supλ⪰0,ν⟮f0(x)+∑i=1mλifi(x)+∑i=1pνihi(x)⟯j(x)=supλ⪰0,νL(x,λ,ν)=supλ⪰0,ν⟮f0(x)+∑i=1mλifi(x)+∑i=1pνihi(x)⟯

关于惩罚的思维在原始问题中同样适用，例如如果有某个xx违反了原始问题的约束条件，假设存在某个ii使得约束fi(x)>0fi(x)>0时，可以让λi→+∞λi→+∞，同理若存在某个ii使得约束hi(x)≠0hi(x)≠0时，可以让νihi(x)→+∞νihi(x)→+∞，而将其余的λλ与νν均变成0，造成g(λ,ν)→+∞g(λ,ν)→+∞不收敛。如果xx能同时满足等式与不等式约束，根据对偶性质可知j(λ,ν)=f0(x)j(λ,ν)=f0(x)，即有： 

j(x)={f(x),+∞,    x满足原始问题的约束    其他j(x)={f(x),    x满足原始问题的约束+∞,    其他

下面考虑极小化问题，类似的得知 j(x)j(x) 是凸的，因此有： 

  minx j(x)=minxmaxλ⪰0,ν L(x,λ,ν)s.t.   λi⪰0  minx j(x)=minxmaxλ⪰0,ν L(x,λ,ν)s.t.   λi⪰0

这被称为拉格朗日的极小极大问题，经过观察可以发现这个问题与原问题是等价的，他们有相同的解，假设其为p∗p∗.

---

对偶性关系

若原始问题与对偶问题都有最优值，则存在d∗≤p∗d∗≤p∗。证明： 

g(λ,ν)=minxL(x,λ,ν)≤L(x,λ,ν)≤maxλ⪰0,νL(x,λ,ν)=j(x)g(λ,ν)=minxL(x,λ,ν)≤L(x,λ,ν)≤maxλ⪰0,νL(x,λ,ν)=j(x)

即 

g(λ,ν)≤j(x)g(λ,ν)≤j(x)

又因 g(λ,ν)g(λ,ν) 有最优极大值，而 j(x)j(x) 有最优极小值，故有： 

maxλ⪰0,νg(λ,ν)≤minxj(x)maxλ⪰0,νg(λ,ν)≤minxj(x)

所以 

d∗=maxλ⪰0,νg(λ,ν)≤minxj(x)=p∗d∗=maxλ⪰0,νg(λ,ν)≤minxj(x)=p∗

在这里我们要提到两个优化学概念，即 强对偶性 与 弱对偶性 。强对偶性指如果原始问题与对偶问题是等价的，相对地弱对偶性指二者并不等价且原始问题的最优解 大于或等于 对偶问题的最优解（这个差被称为“ 对偶间隙 ” p∗−d∗p∗−d∗ ）。

---

KKT条件的几何解释

上面我们谈了很多繁琐复杂的定义与数学关系。在这部分我尝试用简洁的语言探讨拉格朗日问题的几何意义。

首先考虑等式约束。让我们从不失一般性的最简单模型开始，可以很轻松的推广到更复杂的模型。我们首先假设一个最简单的凸优化问题，带有一个等式约束： 

 minf(x)s.t. h(x)=0 minf(x)s.t. h(x)=0

由此构造拉格朗日函数 L(x,ν)=f(x)+νh(x)L(x,ν)=f(x)+νh(x) . 对于目标函数，由凸性可知其最优解发生在 ∇f(x)=0∇f(x)=0 处，并且拉格朗日函数的最优解发生在 ∇f(x)+ν∇h(x)=0∇f(x)+ν∇h(x)=0 处。显然，因为拉格朗日函数的引入，最优解的位置发生了一些偏移，即 ∇f(x)=−ν∇h(x)∇f(x)=−ν∇h(x) 。 假设我们的解 xx 在优化的过程中，改变量为 ΔxΔx ，即每次迭代更新时解会从 xx 更新到 x+Δxx+Δx 。原问题中的等式约束在 DD 维空间内是一个光滑的超平面（ h(x)=0h(x)=0 流形）。而 xx 的每次更新为了保证满足等式约束，所以要发生在这个光滑的超平面上，即方向 ΔxΔx 必须与这个超平面的梯度方向保持正交，因此有 ΔxT∇h(x)=0ΔxT∇h(x)=0 并且 ΔxT∇f(x)ΔxT∇f(x) 不等于0。保持移动 xx ，最终可以到达一个最优点使 ∇f(x)=−ν∇h(x)∇f(x)=−ν∇h(x) ，即在这个最优点上 f(x)f(x) 的梯度与 h(x)h(x) 的梯度保持平行，由于对 νν 值没有特别的约束，故可以朝向相反方向，也可以相同方向。

情况对于不等式约束会复杂一点。这里涉及到一个优化学概念叫互补松弛[^footnote]。我们可以同样写出带有一个不等式约束的凸优化问题： 

 minf(x)s.t. g(x)≤0 minf(x)s.t. g(x)≤0

构造拉格朗日函数有 L(x,λ)=f(x)+λg(x)L(x,λ)=f(x)+λg(x) 。类似的拉格朗日函数最优点发生在 ∇f(x)+λ∇g(x)=0∇f(x)+λ∇g(x)=0 处。 

 
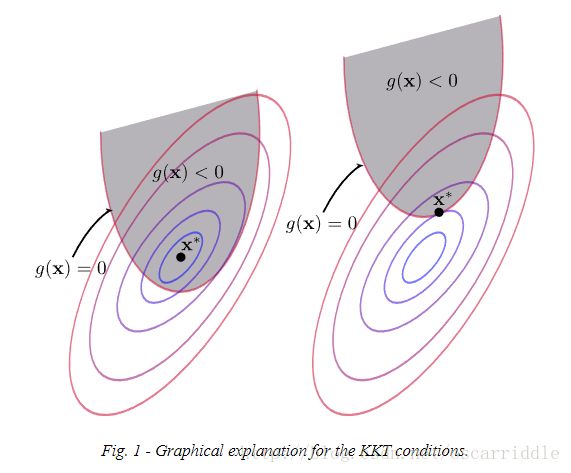
如图1，此时我们要分两种情况讨论。第一种情况是当最优解发生在 g(x)g(x)的表面上时（ g(x)=0g(x)=0）。这意味着此时只可能 ∇f(x)∇f(x)与 ∇g(x)∇g(x)平行且指向相反的方向，因为梯度方向是函数增长的最快的方向所以我们优化的方向只能是 −∇f(x)−∇f(x)。如果二者平行且指向同一方向，我们的x沿着 −∇f(x)−∇f(x)方向前进时，会减小 f(x)f(x)值的同事，也减少 g(x)g(x)的值，造成 xx移动到 g(x)<0g(x)<0的内部区域内，就不在表面上了。总结一下，在不等式约束条件中，若最优点发生在不等式超体表面，则需要有 λ>0λ>0。 
 
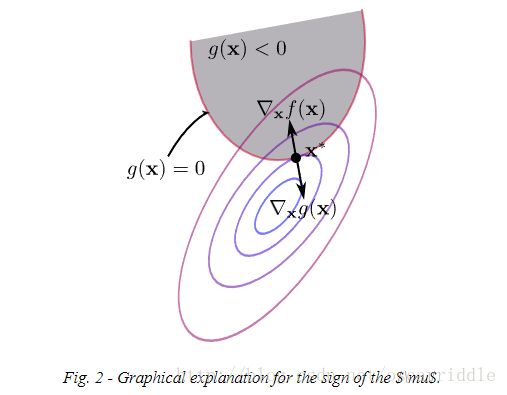
第二种情况是当最优解 x∗x∗发生在 g(x∗)<0g(x∗)<0时。即不等式严格成立时，我们可以将这一项从拉格朗日函数中去掉，因为此时最优解已经可以通过 ∇f(x)=0∇f(x)=0得到，不需要额外引入约束条件，所以此时 λ=0λ=0。这通常被称为“互补松弛”。

以上的分析构成了KKT条件的几何描述，KKT条件保证了拉格朗日问题与原始问题的解是等价的。

原始问题约束： fi(x)≤0,i=1,...,m,hi(x)=0,i=1,...,pfi(x)≤0,i=1,...,m,hi(x)=0,i=1,...,p 
对偶问题约束： λ⪰0λ⪰0 
互补松弛： λifi(x)=0,i=1,...,mλifi(x)=0,i=1,...,m 
拉格朗日极值点：∇L(x,λ,ν)=∇f0(x)+∑mi=1λi∇fi(x)+∑pi=1νi∇hi(x)=0∇L(x,λ,ν)=∇f0(x)+∑i=1mλi∇fi(x)+∑i=1pνi∇hi(x)=0

以上就构成了KKT条件的定义，当KKT条件满足时，拉格朗日问题与原问题是等价的，也就构成了我们之前所提到的强对偶。另一个有趣的是，当KKT条件满足时（或原问题与对偶问题是强对偶时），参数λλ与νν被称为拉格朗日乘子。

---

敏感度问题

KKT问题有非常多可以分析的话题，这里简单介绍一个敏感度问题，有兴趣的朋友可以继续延伸。如果我们尝试对对偶函数求关于约束的偏微分，可以看到结果是拉格朗日乘子： 

λi=−∂g(λ∗,ν∗)∂fi,  νi=−∂g(λ∗,ν∗)∂hiλi=−∂g(λ∗,ν∗)∂fi,  νi=−∂g(λ∗,ν∗)∂hi

根据我们之前所叙述的，如果 λi=0λi=0 则代表对应的第 ii 个不等式约束被消除掉不再起约束作用。并且乘子 λλ 与 νν 越大代表对应的约束越强，呈正相关，此时对约束的一点点小小的改变都对整个目标函数产生巨大的影响。在经济学原理中，对偶乘子 λλ 与 ν

ν也被称为“影子价格”。

参考

https://blog.csdn.net/oscarriddle/article/details/78790135