数据结构（廿一） -- C语言版 -- 图 - 图的基本概念

零、读前说明

• 本文中没有涉及到很多的相关理论知识，也没有做深入的了解，所以，您如果是想要系统的学习、想要多学习关于理论的知识等，那么本文可能并不合适您。
• 本文中所有设计的代码均通过测试，并且在功能性方面均实现应有的功能。
• 设计的代码并非全部公开，部分无关紧要代码并没有贴出来。
• 如果你也对此感兴趣、也想测试源码的话，可以私聊我，非常欢迎一起探讨学习。
• 由于时间、水平、精力有限，文中难免会出现不准确、甚至错误的地方，也很欢迎大佬看见的话批评指正。
• 嘻嘻。。。。 。。。。。。。。收！

一、概述

  日常生活中，出门在外，少不了怎么走，去哪儿的问题，在现在条条大路通罗马的情况下，更少不了好好规划选择合适的方式。而在不熟悉路况的情况下，某某导航简直就是神仙，那在这些中，“图” 或多或少的扮演者重要的角色。

  关于图的内容与知识过于庞大和复杂，我们浅尝辄止，切勿过分沉迷！！！

  图（ Graph）是一种较线性表和树更为复杂的数据结构，在线性表中，数据元素之间仅有线性关系，每个数据元素只有一个直接前驱和一个直接后继；在树形结构中 ，数据元素之间有着明显的层次关系，并且每一层上的数据元素可能和下一层中多个元素（即其孩子节点）相关 但只能和上一层中一个元素（即其双亲节点） 相关，而在图形结构中，结点之间的关系可以是任意的 ，图中任意两个数据元素之间都可能相关。

  下面首先来看看几个示意图，如下图所示。
  

图 1.1 示意图

  
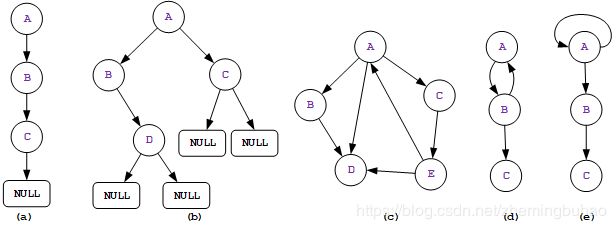
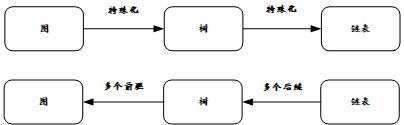
  右上图中可以看出来，(a)为线性表（链表），(b)为树，(c)、(d)、(e)分别为图，同样地，线性表和树也可以看做是一种特殊的树。其中关系可以表示为下图这样。

图 1.2 线性表、树、图的关系示意图

  
  相对于线性结构和树结构，图对元素的限定少，所以图用来描述应用问题的能力也就相对强。

二、图的定义以及相关概念

2.1、图的定义

  图 （ Graph）是由顶点的有穷非空集合和顶点之间边的有穷集合组成。通常可以表示为 $$Graph=(V,E)$$  其中：
    $V：V=\{x|x\in 数据对象\}$, 图的顶点的有穷（有限个）非空（至少有一个）集合
    $E：E=\{(x,y)|x,y\in V\}$，顶点与顶点之间的关系的有穷集合，也叫作边（ Edge）集合

  将 顶点的集合的数量 记做 $n$，那么 $n=|V|$
  将 边集合的数量 用 $e$ 来表示，那么 $e=|E|$

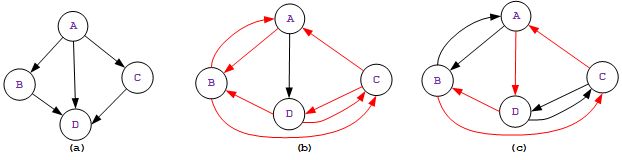
  所以，上图1.1中所有图例均为“ 图 ”（点我查看图1.1详情）。

  需要数以的几个地方：

  1、线性表中我们把数据元素叫元素，树中将数据元素叫节点 ，在图中数据元素就们则称之为顶点（Vertex)

  2、线性表中可以没有数据元素，没有元素的称为空表，在树中也可以没有节点称为空树，但是在图中，非常强调是非空，也就是没有空图

  3、线性在中相邻的数据元置之间具有钱性关系，树结构中相邻两层的节点具有层次关系 ，而在图中任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的

2.2、有向和无向

  首先，如下图所示，分别来表示无向边（图）、有向边（图），混合图。

图 2.1 无向、有向，混合示意图

  
  无向：两个顶点 $V_i$ 和 $V_j$ 构成 边的没有方向，顶点 $V_i$ 和 $V_j$ 没有具体的先后问题，只用来表示 $V_i$ 和 $V_j$ 的链接关系，则称呼 $V_i$ 和 $V_j$ 形成的边 ( $V_i$ , $V_j$ ) 或者 ( $V_j$ , $V_i$ ) 为无向边( Undirected edge，用圆括弧来表示)。 如果所有边均为无向边所构成的图，称为无向图。
  比如：A 是 C 是好朋友，同样 C 也是 A 的好朋友

  有向：构成边的两个顶点 $V_i$ 和 $V_j$ 有具体的先后问题 ，并且< $V_i$ , $V_j$ >和< $V_j$ , $V_i$ >表示不同的含义 则称呼 $V_i$ 和 $V_j$ 形成的边为有向边(用尖括弧来表示，也称为 弧 )。如果所有边均为有向边所构成的图，称为有向图 。那对于边< $V_i$ , $V_j$ >, 称 $V_i$ 为尾， $V_j$ 为头
  比如： A 欠 D 的金钱

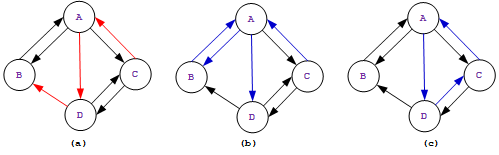
  混合：如果一个图中，有一些边是有向的，有一些边是无向的，称之为混合图（mixed graph ），在实际表示中，可以用有向图来表示无向图以及混合图，只需要：将任何一条无向边转换为彼此对称的一对有向边，如下图所示。
  

图 2.2 无向转有向示意图

  
  简单图：在图中不存在顶点到自身的边，且同一条边只出现一次。

图 2.3 无向完全图、有向完全图示意图

  
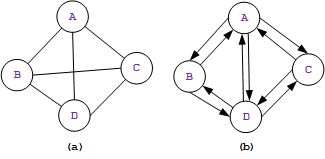
  无向完全图：指的是在无向图中，如果任意两个顶点之间都存在边的图（上图1.5中(a)）。

    无向完全图含有 $n$ 个顶点的无向完全图有 $\frac{n\times (n-1)}{2}$ 条边。

  有向完全图：指的是在有向图中，如果任意两个顶点之间都存在方向互为反向的两条边的图（上图1.5中(b)）。

    有向完全图含有 $n$ 个顶点的有向完全图有$n\times (n-1)$条边。

2.3、邻接关系和关联关系

  邻接关系：顶点与顶点之间的关系，对应于顶点与顶点的关系。

    对于线性的结构，只有 互为前驱和后继 的元素节点才能定义这种邻接关系
    对于树结构，也只有 父节点与子节点 之间可以定义邻接关系
    图中允许 任意两个节点 之间存在邻接关系，但是也有一种特殊情况，一个元素与自身形成邻接关系（上图1.1中(e)所示）（点我查看图1.1详情）。

  关联关系：参与定义这种邻接关系的每一个顶点与这个邻接关系之间的关系，对应于顶点与边的关系。

  对于 无向图 $G=(V,E)$，如果边 $(V1,V2)\in E$，则成顶点 $V1$ 和 $V2$ 互为 邻接点，即 $V1$ 和 $V2$ 邻接。边 $(V_1,V_2)$ 依附于顶点 $V1$、$V2$ ，也就是说边 $(V_1,V_2)$ 与顶点 $V_1$、$V_2$ 相关联。

2.4、度

  顶点 $V$ 的度是和 $V$ 相关联的边的数目，记为 $TD(v)$，比如上图1.1中图(a)中，和顶点 A 相关的边有 3 条，所以顶点 A 的度为 3。

  对于有向图，还有入度和出度的区别。

    入度：以 $V$ 为 头 的边的数目，记为 $ID(v)$，比如上图1.1中(b)所示， A 的入度为 1。
    出度：以 $V$ 为 尾 的边的数目，记为 $OD(v)$，比如上图1.1中(b)所示， A 的出度为3。

  根据上面的说明，在一个有向图中，我们可以得出下列的简单总结：

  1、顶点度等于出度和入度之和，即 $TD(v)=ID(v)+OD(v)$

  2、图中边的数目等于顶点的度的和的一半，即 $E=$ $\frac{(TD(v_1)+TD(v_2)+\dots +TD(v_n))}{2}$

  3、边的数目等于所有顶点的入度的和，即 $E=ID(v_1)+ID(v_2)+\dots +ID(v_n)$

  4、边的数目等于所有顶点的出度的和，即 $E=OD(v_1)+OD(v_2)+\dots +OD(v_n)$

2.5、路径和环路

  首先，来一张图来表示，然后再开始说。

图 2.4 简单路径、环的示意图

  
  路径：由一系列的顶点按照依次邻接的关系组成的序列，表示为 $\pi =<v_0,v_1,\dots v_m>$ ，路径的长度 $|\pi |=m$

  比如：从顶点 “C -> A -> D -> B” 的过程，构成了一个长度为 3 的路径。像这样不含重复节点的路径，称为简单路径（ simple path ）。再比如：从顶点 "C -> A -> B -> A -> D"的过程，构成了一个长度为 4 的路径，但是路径中同一个顶点出现了 2 次，称之为 不简单路径 或者 路径。

  如果出现 $v_0=v_m$，则形成 环/环路。

  比如图中路径 “C -> A -> D -> C” 形成 环路
  再比如图中路径 “C -> A -> B -> A -> C” 同样形成 环路

  同样的，不包含重复的顶点则称为简单环路，否则为不简单环路或者环路。

  再来一张图片，如下图所示。

图 2.5 有向无环图、欧拉环、哈密尔顿环示意图

  
  如果在一个有向图中不包含任何环路，则称之为 有向无环图（上图2.5中(a)所示）。

  从任何一个顶点出发，将所有的边组成一个环路，这样经过所有的边 一次而且恰好一次 的环路称为 欧拉环路（ Eulerian tour，上图2.5中(b)所示）。

  经过每一个顶点一次，而且 恰好一次（ “C -> A -> D -> B -> C” ），则称之为 哈密尔顿环路（ Hamiltonian tour，上图2.5中(c)所示 ）。

  权 (weight)：和边相关的数字，通常用来表示顶点之间的距离或者耗费。这种带权的图通常称为网（ Network）。

2.6、子图

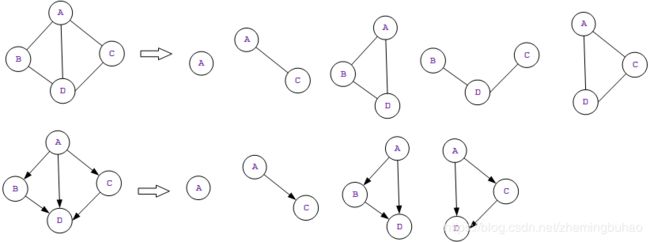
  假设有两个图分别为 $Grap{h}_1=(V_1,E_2)$ 和 $Grap{h}_2=(V_2,E_2)$ ，如果顶点 $V_2\subseteq V_1$ 并且 $E_2\subseteq E_1$, 那么称 $Grap{h}_1$ 为 $Grap{h}_2$ 的 子图（subGraph）。

  比如下图所示，箭头右边的均为左边的子图。

图 2.6 子图示意图

  

2.7、连通图

  在 无向图 $Graph$ 中，如果从顶点 $V_1$ 到顶点 $V_2$ 有路径，则称为 $V_1$ 和 $V_2$ 是 连通 的。

  如果对于图中 任意两个顶点 $V_i$ 和 $V_j$ 都是连通的，则称 $Graph$ 是 连通图（connectedGraph），如上图 2.3 中 （a） 所示（点我查看图2.3详情）。

  连通分量：无向图中的极大连通子图

  在 有向图 $Graph$ 中，如果对于 每一对 $V_i$ 和 $V_j$ 都存在路径，则称 $Graph$ 为 强连通图。

  有向图 中极大强连通子图称为有向图的强连通分量。

  比如下图中 (a) 为 强连通图，并且 (a) 为 (b) 的极大强连通图，也是其强连通分量。

图 2.7 极大强连通图示意图

  
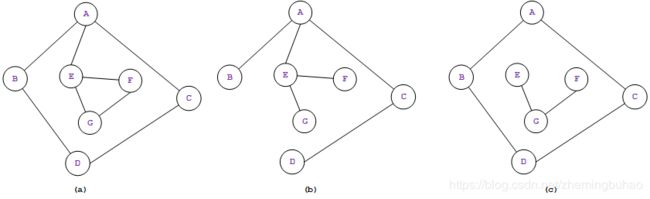
  连通图的生成树：指的是一个 极小的联通子图，含有图中 全部的顶点 (比如有 $n$ 个顶点 )，但是只有足以构成一棵树的 $n-1$ 条边。

  如下图所示，图 (a) 中的图有 7 个顶点，但是 8 条边，如果想要成为生成树的话，需要删除两条边，如图 (b) 所示即为生成树，但是同样的去掉原本图中的两条边，如图 (c) 所示，就不是生成树。

图 2.8 生成树示意图

  
  所以， 满足 $n$ 个顶点 $n-1$ 条边的图，不一定就是 生成树，但是生成树一定满足 $n$ 个顶点 $n-1$ 条边。

  如果有一个 有向图恰有一个顶点入度为0，其余顶点的入度均为1，则是一个有向树。

  如下图所示中 (a) 为一个普通的有向图，其中还有 7 个顶点， 10 条边，那么删除 (a) 中的部分边，让其满足n-1的条件（需要删除 4 条边），删除后如 (b) 所示。那么在 (b) 中，就是一个生成的 有向树。

图 2.9 生成有向树示意图

三、简单的总结

  从上一篇 霍夫曼树 到现在，经历了很长的时间，一者项目处于紧要时期比较忙，业余时间少；二者图部分的内容用的比较少，虽然在以前图相关的内容曾经学过，虽也学的一知半解，所以基本上属于大白的状态。所以迟迟没有开始。

  细回想当初开始编写数据结构相关博客的时候，由于在二月份开始居家办公时间，业余时间比较宽裕，但是从三月份开始办公室办公，工作内容繁杂基本没有什么空闲时间，但是一直坚持每天一个字一个字的更新博客，也基本上保证每周更新一篇博客，一直到现在才将顺序表链表栈队列树的内容完成，虽然数量有限但是保证写的详细、力争无错误。虽然源码没有全部贴出来，但是各种测试案例测试效果保质保量。

  总结各种知识点，不光要参考各种书本，还要自己理解并加以描述，其实是很枯燥的，而且本来图这部分内容相当于重新学习一遍，所以进度很缓慢。虽然阅读量不曾增加也貌似没什么评论或者鼓励的，但是于己于人，我想我都会坚持下去，坚持将基本的数据结构、基本的排序等用自己的方式总结出来。加油吧！！！

  好啦，废话不多说，总结写作不易，如果你喜欢这篇文章或者对你有用，请动动你发财的小手手帮忙点个赞，当然 关注一波 那就更好了，好啦，就到这儿了，么么哒(* ￣3)(ε￣ *)。

上一篇：数据结构（二十） – C语言版 – 树 - 霍夫曼树（哈夫曼树、赫夫曼树、最优二叉树）、霍夫曼编码
下一篇：数据结构（廿二） – C语言版 – 图 - 图的存储结构 – 邻接矩阵