姿态解算(用于飞行器或ROV等)的基本思路和数学原理

（一）前言

  数学是算法的门槛
  我们就用数学的角度去探寻姿态解算，不谈代码
  主要是了解这其中用到的数学思想
  学完这个你就会感叹，MPU的DMP真香…

  本文我们只能非常简单基础的谈谈这其中的数学原理
  在学习之前，你需要记住个这图——记住这三个角度。这三个角度就是我们苦苦追寻。

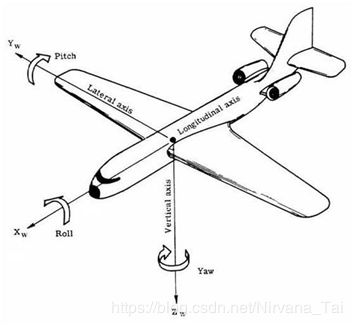
  一个小法术：你会回来的。
  那么正片开始。

（二）方向余弦矩阵DCM

  这里我们引入一个概念——DCM

  将原坐标系定义为Oxyz，旋转而成另外一个坐标系定义为OXYZ，两坐标系的具有相同的原点O，如下图。
  本体坐标系的x、y、z轴对应的单位向量分别为i，j，k；全局坐标系X、Y、Z轴对应的单位向量分别为I，J，K

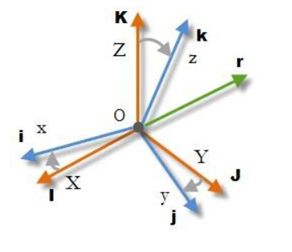
  方向余弦矩阵即表示两个坐标轴之间的转换系数
  方向余弦矩阵是由本体坐标系和全局坐标系单位向量所有可能组合的角度的余弦组成
  直接给出方向余弦矩阵的方程可能不好理解，所以将旋转分为三个自由度上的各自旋转再叠加

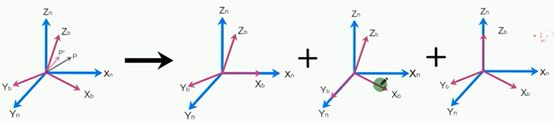
（我是用的别人的图啊，画太麻烦了，说明清楚就行了，不要在意坐标系定义符号的变换）
  这张图展示的过程就是原坐标系绕原点旋转到另一坐标系的分解过程。
①绕X旋转：旋转系数矩阵为

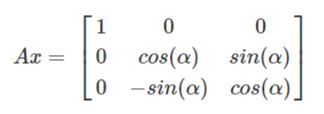
②绕Y旋转：旋转系数矩阵为

③绕Z旋转：旋转系数矩阵为

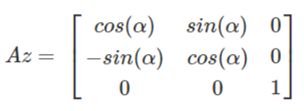
  最终，整个的变化的系数矩阵为A=Ax∗Ay∗Az，即为方向余弦矩阵
A=

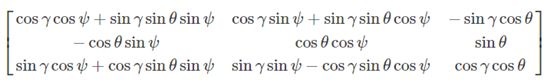
  当然，根据转换角度选择的不同，可能有不同形式的方向余弦矩阵，但原理相同。
  注意，这个方向余弦矩阵是正交的。
记

  那么，它的转置矩阵

  此时，我们有一种方式去求三个欧拉角。即为

参考蔡永元老师的《惯性导航》

  但这种求法会有两个巨大的缺陷：
①方程自变量与因变量同纲，方程无法求解。当俯仰角为90度时方程式会出现神奇的“GimbalLock”（万向锁）
②过多三角函数的参与运算是运算求解过于复杂，十分影响运算速度。
  所以，我们直接摒弃这种求法。

看到这里，你只需要知道DCM是如何定义得到的和表达形式就可以了。

（三）四元数

  这里，我们在引入一个概念——四元数
  四元数是哈密顿为了描述三维空间旋转而引入的，可以去百度一下它的来源和具体推导，这里只是很肤浅地应用一下
  因为四元数是超球面，是个四维概念。我们可能难以理解，这里贴一篇文章，能够清晰地讲述四元数的可视化。【很好的演示】https://eater.net/quaternions/
  四元数有很多表达形式，比如
  一般形式Q= q0+q1i+q2j+q3k
  矩阵形式
  三角函数形式：Q=cosθ/2+λsinθ/2 ——注意这个三角函数的形式
  那么如何将四元数与DCM相联系呢，我们引入罗德里格旋转的概念
  罗德里格旋转的坐标系建立比较特殊，它是以原向量，旋转轴及它们叉积作为坐标轴建立的

  通过很多推导，我们可以把利用四元数的三角函数形式

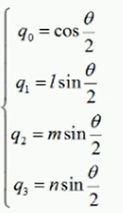
  就可以用四元数去替换DCM中的三角函数

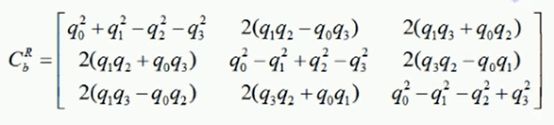
  这时，对于三个欧拉角的求解可简化为

  那现在，要求出三个欧拉角只需要知道四元数得值。

（四）求四元数

更新四元数

  这里需要先说明一个概念，四元数是时间相关的函数
  那么，我们对四元数对时间求微分，可以得到这么一个微分方程：

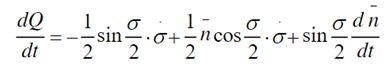
  对微分方程求解，可以得到：

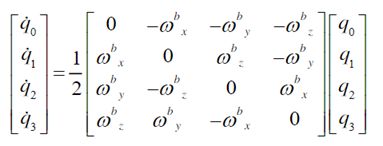
  由于四元数是时变的，为我们需要用计算机对其运算求解，则必须转换为离散模型去进行对四元数的更新
  这里使用一阶龙格库塔法模型去求解，这是一种工程中常用的求解微分方程的算法

  便得到：

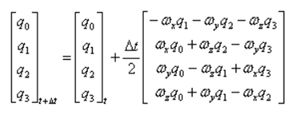
  其中，wx,wy,wz分别表示载体坐标系相对于大地坐标系沿各个轴向的角速度分量

  现在，问题转换到角度的求解

  有两种常用的角度求解方式。
①利用角速度的积分，可以得到角度。但会因为积分漂移产生低频误差。
②利用加速度正交求解，可以得到角度，但会因为振动误差而产生高频误差。

而这些计算不可避免地会出现一些误差。对于陀螺仪获取角速度取积分得到角度，在长时间下积分偏离会造成较大误差。

误差消除

  现在有常用的三种误差消除的方式。
  其实，你只需要知道这么多消去误差的方法，核心就是预测+测量反馈

①互补滤波法（PI算法）：
  简洁地介绍一下：所谓互补，就是用加速度计的数据去矫正陀螺仪的积分出来角度。我们可以暂时相信加速度计，但他的动态响应不太理想。所谓滤波，就是滤去陀螺仪的低频信号，滤去加速度计的高频信号。
  而去补偿的思想采用了PI算法。PI算法大家可以看我的其他博文，这个基础的很简单，不会的私我，我给你看看代码。

  这里提一下向量外积的概念。

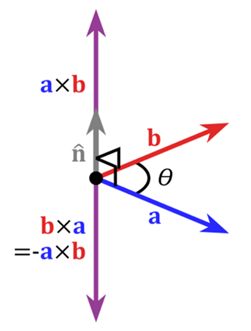
  这里a是陀螺仪计算值，b是加速度计算值。从而角度θ便是偏差。我们用向量外积去求出这个角度。而用PI算法去补偿误差。
  简单贴一下工程中的互补滤波算法代码，可以理解一下。

float ComplementaryFilter(float angle_m, float gyro_m)
{
    gyro_m -= 0.35;
    angleyy = K1 * angle_m + (1-K1) * (angleylast + gyro_m * dtt);
    angleylast = angleyy;
    return angleyy;
}

互补滤波请参考https://blog.csdn.net/seek97/article/details/81294097

②mahony算法（地磁计融合补偿）：
具体参考请https://blog.csdn.net/yzhajlydy/article/details/21870197

③卡尔曼滤波法（最小均方误差）：
  这是现在最常用的一种滤波法，它的效果也是最好的。
  它的核心就是力求均方误差最小
  具体的推导原理请看https://blog.csdn.net/heyijia0327/article/details/17487467
  这里给出一下思路，方便代码理解：
  首先要计算预测值、预测值和真实值之间误差协方差矩阵。

  有了这两个就能计算卡尔曼增益K，再然后得到估计值，

  最后还要计算估计值和真实值之间的误差协方差矩阵，为下次递推做准备。

  贴一下工程中的代码，一个角度上的卡尔曼滤波算法，仅供理解：

float AccX_KalmanFilter(const float ResrcData,float ProcessNiose_Q,float MeasureNoise_R,float InitialPrediction)
{
	float R = MeasureNoise_R;
	float Q = ProcessNiose_Q;
	static	float x_last;
	float x_mid = x_last;
	float x_now;
	static	float p_last;

	float p_mid ;
	float p_now;
	float kg;	

	x_mid=x_last;
	p_mid=p_last+Q; 
	kg=p_mid/(p_mid+R);	x_now=x_mid+kg*(ResrcData-x_mid);
		
	p_now=(1-kg)*p_mid;

	p_last = p_now; 
	x_last = x_now; 

	return x_now;		
}

（五）总结

  好了。本文就介绍这么多。

  我总结一下姿态解算的步骤：
  先说一下已知量：陀螺仪可以得到三个轴的角速度，加速度计可以获取三个轴的加速度原始数据。

①初始四元数。
①更新四元数。补偿更新四元数
②用四元数算出欧拉角。

  最后推荐一篇文章，如果你想更加细节的学习，这篇文章会更好的帮助你
https://wenku.baidu.com/view/218c876d856a561253d36f2a.html
  秦永元老师的《惯性导航》也是非常细致的解释了四元数和其推导和计算。
  如果你想在在工程中运用，建议看IMU中的源码。和匿名科技对于飞控姿态解算的开源代码。
  谢谢，整理编写不易，请留个赞！