各种加密算法内部原理实现
众所周知数据对于一个公司来说,非常重要,一旦数据泄露,公司将面临非常大的威胁,因此对数据加密非常有必要,保证数据的安全性。
1 加密算法的基本原理
加密算法目前主流分为对称加密,不对称加密,散列加密。
1.1 对称加密
对称加密是指加密和解密使用相同密钥的加密算法,常见的对称加密算法有DES,DES3,AES加密算法。对称加密由于其加解密速度快,常被用于大量的数据加密场景,还有对传输效率要求高的场景如VPN之间的传输,但是由于其密匙不方便保存,所以适合于内部系统。
1.1.1 DES加密算法
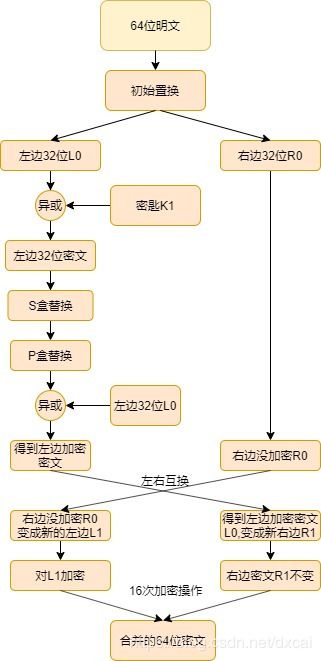
DES加密算法是一种分组加密算法,通过将输入的明文按64位一组,进行分组加,加密过程分为初始置换明文,分组明文,生成子密匙,密匙与明文加密,经过S盒替换,P盒替换,置换后的密文与原32位明文加密。
初始置换:初始置换是只将输入的64位明文,按照一个置换表进行置换位置,具体置换规则:初始数据里面的64是1号位,置换表的1则到了第40这个位置,那么64置换之后就到了第40这个位置、63是原来的2号位,在置换表里面是第8号位,所以63经过置换表则到了第8位,其他的位置执行同样的操作,具体操作如表1.1,表1.2,表1.3:
表1.1 初始数据表
| 64 |
63 |
62 |
61 |
60 |
59 |
58 |
57 |
| 26 |
55 |
54 |
53 |
52 |
51 |
50 |
49 |
| 48 |
47 |
46 |
45 |
44 |
43 |
42 |
41 |
| 40 |
39 |
38 |
37 |
36 |
35 |
34 |
34 |
| 32 |
31 |
30 |
29 |
28 |
27 |
26 |
25 |
| 24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
| 16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
表1.2 置换表
| 58 |
50 |
42 |
34 |
26 |
18 |
10 |
2 |
| 60 |
52 |
44 |
36 |
28 |
20 |
12 |
4 |
| 62 |
54 |
46 |
38 |
30 |
22 |
14 |
6 |
| 64 |
56 |
48 |
40 |
32 |
24 |
16 |
8 |
| 57 |
49 |
41 |
33 |
25 |
17 |
9 |
1 |
| 59 |
51 |
43 |
35 |
27 |
19 |
11 |
3 |
| 61 |
53 |
45 |
37 |
29 |
21 |
13 |
5 |
| 63 |
55 |
47 |
39 |
31 |
23 |
15 |
7 |
表1.3 置换后数据
| 7 |
15 |
23 |
31 |
39 |
47 |
55 |
63 |
| 62 |
54 |
46 |
38 |
30 |
22 |
14 |
6 |
| 3 |
11 |
18 |
27 |
35 |
43 |
51 |
59 |
| 1 |
9 |
17 |
25 |
33 |
41 |
49 |
57 |
| 8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
| 6 |
14 |
22 |
30 |
38 |
46 |
54 |
62 |
| 4 |
12 |
20 |
28 |
36 |
44 |
52 |
60 |
| 2 |
10 |
18 |
26 |
34 |
42 |
50 |
58 |
拿到置换后的数据后,将明文分组左右两组。将初始置换之后的数据按前32位为左边L0,后32位为右边R0。具体分组如表1.4,1.5.
表1.4 左边L0
| 7 |
15 |
23 |
31 |
39 |
47 |
55 |
63 |
| 62 |
54 |
46 |
38 |
30 |
22 |
14 |
6 |
| 3 |
11 |
18 |
27 |
35 |
43 |
51 |
59 |
| 1 |
9 |
17 |
25 |
33 |
41 |
49 |
57 |
表1.5 右边R0
| 8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
| 6 |
14 |
22 |
30 |
38 |
46 |
54 |
62 |
| 4 |
12 |
20 |
28 |
36 |
44 |
52 |
60 |
| 2 |
10 |
18 |
26 |
34 |
42 |
50 |
58 |
将一个主密匙生成16个子密匙,每一次操作用一个密匙。用户设置的一个64位key,我们将其忽略第8,16,24,32,40,48,56,64奇偶检验位。得到一个56位key,将其进行移位操作,再进行压缩置换就得到具体加密的KEY。具体操作如表1.6 所示
表1.6 移位操作是移位表
| 移位表 |
||||||||||||||||
| 轮询次数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 移动位数 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
从表中我们可以知道,第一轮是左移一位,第三轮是左移两位,后面一堆位数安装表1.6所示即可。具体移位如表1.7,表1.8
表1.7 主密匙表
| 57 |
49 |
41 |
33 |
25 |
17 |
9 |
1 |
| 58 |
50 |
42 |
34 |
26 |
18 |
10 |
2 |
| 59 |
51 |
43 |
35 |
27 |
19 |
11 |
3 |
| 60 |
52 |
44 |
36 |
63 |
55 |
47 |
39 |
| 31 |
23 |
15 |
7 |
62 |
54 |
46 |
38 |
| 30 |
22 |
14 |
6 |
61 |
53 |
45 |
37 |
| 29 |
21 |
13 |
5 |
28 |
20 |
12 |
4 |
表1.8 左移一位后的密匙
| 49 |
41 |
33 |
25 |
17 |
9 |
1 |
57 |
| 50 |
42 |
34 |
26 |
18 |
10 |
2 |
58 |
| 51 |
43 |
35 |
27 |
19 |
11 |
3 |
59 |
| 52 |
44 |
36 |
63 |
55 |
47 |
39 |
60 |
| 23 |
15 |
7 |
62 |
54 |
46 |
38 |
31 |
| 22 |
14 |
6 |
61 |
53 |
45 |
37 |
30 |
| 21 |
13 |
5 |
28 |
20 |
12 |
4 |
29 |
移位之后进行压缩置换,将56位的密匙进行48位的置换表置换,得到48位密匙舍去8位,如表1.9,1.10,表1.11所示
表1.9 密匙
| 49 |
41 |
33 |
25 |
17 |
9 |
1 |
| 57 |
50 |
42 |
34 |
26 |
18 |
10 |
| 2 |
58 |
51 |
43 |
35 |
27 |
19 |
| 11 |
3 |
59 |
52 |
44 |
36 |
63 |
| 55 |
47 |
39 |
60 |
23 |
15 |
7 |
| 62 |
54 |
46 |
38 |
31 |
22 |
14 |
| 6 |
61 |
53 |
45 |
37 |
30 |
21 |
| 13 |
5 |
28 |
20 |
12 |
4 |
29 |
表1.10 48位置换表
| 14 |
17 |
11 |
24 |
1 |
5 |
| 3 |
28 |
15 |
6 |
21 |
10 |
| 23 |
19 |
12 |
4 |
26 |
8 |
| 16 |
7 |
27 |
20 |
13 |
2 |
| 41 |
52 |
31 |
37 |
47 |
55 |
| 30 |
40 |
51 |
45 |
33 |
48 |
| 44 |
49 |
39 |
56 |
34 |
53 |
| 46 |
42 |
50 |
36 |
29 |
32 |
表1.11 置换之后得到的数据KEY1
| 1 |
15 |
34 |
60 |
9 |
17 |
| 33 |
19 |
2 |
9 |
10 |
42 |
| 3 |
35 |
26 |
25 |
44 |
58 |
| 59 |
57 |
36 |
27 |
18 |
41 |
| 22 |
28 |
39 |
54 |
37 |
4 |
| 47 |
30 |
5 |
53 |
23 |
22 |
| 61 |
14 |
38 |
21 |
15 |
12 |
| 45 |
7 |
13 |
62 |
55 |
31 |
得到48位密匙后,因为明文分组是32位,所以对明文进行扩充置换成48位,以下操作是对明文进行扩充置换,对于扩充后的明文我们可以发现,他中间四列是原来的明文,并没有修改,增加的第一列是原明文的最后一列从倒数排列,新添加的第后一列,则是第一列的倒数。具体如表1.12,表1.13所示。
表1.12 左边明文L0
| 7 |
15 |
23 |
31 |
| 39 |
47 |
55 |
63 |
| 5 |
13 |
21 |
29 |
| 37 |
45 |
53 |
61 |
| 3 |
11 |
18 |
27 |
| 35 |
43 |
51 |
59 |
| 1 |
9 |
17 |
25 |
| 33 |
41 |
49 |
57 |
表1.13 扩充之后的明文L0
| 57 |
7 |
15 |
23 |
31 |
39 |
| 31 |
39 |
47 |
55 |
63 |
5 |
| 63 |
5 |
13 |
21 |
29 |
37 |
| 29 |
37 |
45 |
53 |
61 |
3 |
| 61 |
3 |
11 |
18 |
27 |
35 |
| 27 |
35 |
43 |
51 |
59 |
1 |
| 59 |
1 |
9 |
17 |
25 |
33 |
| 25 |
33 |
41 |
49 |
57 |
7 |
现在得到48位密匙和48位数据,就可以进行异或加密操作了。异或操作后面拿到的数据是加密后的数据,我们对此数据进行S盒替换和P盒替换。
S盒替换是将48位的数,分组8组,一组6位,进入S盒,一个S盒6位输入4位输出,及48位出入,进入8个S盒输出只有32位。具体替换如表1.14。
表1.14 S0盒:
| 行\列 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 0 |
14 |
4 |
13 |
1 |
2 |
15 |
11 |
8 |
3 |
10 |
6 |
12 |
5 |
9 |
0 |
7 |
| 1 |
0 |
15 |
7 |
4 |
14 |
2 |
13 |
1 |
10 |
6 |
12 |
11 |
9 |
5 |
3 |
8 |
| 2 |
4 |
1 |
14 |
8 |
13 |
6 |
2 |
11 |
15 |
12 |
9 |
7 |
3 |
10 |
5 |
0 |
| 3 |
15 |
12 |
8 |
2 |
4 |
9 |
1 |
7 |
5 |
11 |
3 |
14 |
10 |
0 |
6 |
13 |
例如:输入为101110 那么他的第一位和最后一位组合10转换位10进制则为2及第2行,中间四为0111转为10进制及为7及第7列,所以第2行,第7列及为2转为2进制及为0010,所以输入101110,输出0010,S盒替换完成。经过S盒换以后就要经过P盒替换了,具体替换过程如下表1.15,1.16,1.17所示
表1.15 S盒替换后的数据
| 7 |
15 |
23 |
31 |
39 |
47 |
55 |
63 |
| 5 |
13 |
21 |
29 |
37 |
45 |
53 |
61 |
| 3 |
11 |
18 |
27 |
35 |
43 |
51 |
59 |
| 1 |
9 |
17 |
25 |
33 |
41 |
49 |
57 |
表1.16 P盒
| 16 |
7 |
20 |
21 |
29 |
12 |
28 |
17 |
| 1 |
15 |
23 |
26 |
5 |
18 |
31 |
10 |
| 2 |
8 |
24 |
14 |
32 |
27 |
3 |
9 |
| 19 |
13 |
30 |
6 |
22 |
11 |
4 |
25 |
表1.17 P盒置换后的数据
| 61 |
55 |
27 |
35 |
33 |
29 |
25 |
3 |
| 7 |
3 |
51 |
9 |
39 |
11 |
49 |
13 |
| 15 |
63 |
59 |
45 |
57 |
17 |
23 |
5 |
| 18 |
53 |
41 |
47 |
43 |
21 |
31 |
1 |
现在我们已经拿到P盒置换后的数据了,再跟我们第一次分组生成的32位左边的数据进行异或操作,这次拿到的数据就是我们第一轮加密后的数据,再进行左右互换,进行同样的加密操作,连续操作16次,加密就算完成了。
加密完成了,接下来就是解密了,解密和加密是同样的操作,输入64位明文,进行初始置换,将KEY倒着进行加密,密匙移位,加密是向左移,那么解密就是向右移,执行同样的操作就可以解密进行解密操作。
1.1.2 AES加密算法
AES加密算法是分组加密,每一组是16字节,是目前主流的高级加密算法。他的加密过程主要分为密匙轮询,字节替代,行移动,列混合,密匙加轮…….以上操作重复10次,就是第一次加密的数据
密匙加轮:用密匙与原文进行异或操作,原文是128位,密文也是128位,首先将主密匙与原文进行异或操作,后面再用主密匙生成40位子密匙。密匙生成过程如下所示:
KEY = 3C A1 0B 21 57 F0 19 16 90 2E 13 80 AC C1 07 BD
初始密匙:
W[0]=3C A1 0B 21
W[1]=57 F0 19 16
w[2]=90 2E 13 80
w[3]=AC C1 07 BD
生成密匙算法:
1.如果i不是4的倍数,那么第i列用如下公式:
W[i]=W[i-4] XOR W[i-1] (XOR表示异或的意思,下同)
2.如果i是4的倍数,那么第i列用如下公式:
W[i]=W[i-4] XOR T(W[i-1])
解释一下T()函数:由三部分组成,字循环,字节替代,轮常量代替异或。
a.字循环:将1个字中的4个字节循环左移1个字节。即将输入字[a0, a1, a2, a3]变换成[a1,a2,a3,a0]。
b.字节代换:对字循环的结果使用S盒进行字节代换。
c.轮常量异或:将前两步的结果同轮常量进行异或。具体如表1.18所示
表1.18 轮询常量表
| 轮询数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 轮询常量 |
01 00 00 00
|
02 00 00 00
|
04 00 00 00
|
08 00 00 00
|
10 00 00 00
|
20 00 00 00
|
40 00 00 00
|
80 00 00 00
|
1B 00 00 00
|
36 00 00 00
|
例如:初始密匙
W[0]=3C A1 0B 21
W[1]=57 F0 19 16
w[2]=90 2E 13 80
w[3]=AC C1 07 BD
计算w[4],w[5],w[6],w[7]
求w[4]的时候,因为4是4的倍数,所以,我们先要求T(W[3])
W[3]= AC C1 07 BD
左移一位 得到 C1 07 BD AC
进入S和字节替换
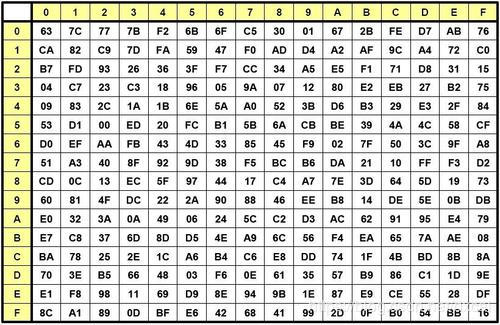
进S盒替换时,例如替换C1,C则是行,1则是列,找到第C行第1列即可以找到替换的数字(16进制的数)S盒
C1在S盒中对应78,
07在S盒中对应C5
BD在S盒中对应7A
AC在S盒中对应 91
所以经过第二步S盒替换变成了78,C5,7A,91
(3).将78 C5 7A 91 XOR 01 00 00 00 = 79 C5 7A 91
所以计算密匙如下:
W[4]= W[0] XOR T(W[3] ) = 3C A1 0B 21 XOR 79 C5 7A 91 = 45 64 71 B0
W[5]= W[1] XOR W[4] = 57 F0 19 16 XOR 45 64 71 B0 = 12 94 68 A6
W[6]= W[2] XOR W[5] = 90 2E 13 80 XOR 12 94 68 A6 = 82 BA 7B 26
W[7]= W[3] XOR W[6] = AC C1 07 BD XOR 82 BA 7B 26 = 2E 7B 7C 9B
同样的方法计算其他密匙。
有了密匙,将明文与密匙异或运算,接下来进行字节替代。例如,假设我们明文与密匙加轮得到的数据是abcdefghijklmnop具体如表1.19,1.10,1.21所示
表1.19 轮询后的数据
| a |
b |
c |
D |
| e |
f |
g |
h |
| i |
j |
k |
l |
| m |
n |
o |
p |
表1.20 转化为16进制
| 0x61 |
0x62 |
0x63 |
0x64 |
| 0x65 |
0x66 |
0x67 |
0x68 |
| 0x69 |
0x6A |
0x6B |
0x6C |
| 0x6D |
0x6E |
0x6F |
0x70 |
表1.21 S盒替代之后的数据
| 0xD0 |
0xEF |
0xAA |
0xFB |
| 0x43 |
0x4D |
0x33 |
0x85 |
| 0x45 |
0XF9 |
0x02 |
0x7F |
| 0x50 |
0x3C |
0x9F |
0Xa8 |
S盒上就是密匙替换的S盒,(如果出来本就是16进制则不需要转换)将a转为16进制0x61则在S盒中找到第6行第1个数,这个数就是要替换的数,替换其他数也是同样的操作。
接下来就是行移动,列混合就是将每一列移动不同的位数,第一列不移动,第二列移动一位,第三列移动两位,第四列移动三位。具体一位如下表1.22,1.23:
表1.22 移位前的数据
| 0xD0 |
0xEF |
0xAA |
0xFB |
| 0x43 |
0x4D |
0x33 |
0x85 |
| 0x45 |
0XF9 |
0x02 |
0x7F |
| 0x50 |
0x3C |
0x9F |
0Xa8 |
表1.23 移位后的数据
| 0xD0 |
0xEF |
0xAA |
0xFB |
| 0x4D |
0x33 |
0x85 |
0x43 |
| 0x02 |
0x7F |
0x45 |
0XF9 |
| 0Xa8 |
0x50 |
0x3C |
0x9F |
行移动后就是列混合了,列混合就是将行移动后的矩阵乘一个固定矩阵。具体如下表1.24,1.25所示
表1.24 行移动后的数据
| 0xD0 |
0xEF |
0xAA |
0xFB |
| 0x4D |
0x33 |
0x85 |
0x43 |
| 0x02 |
0x7F |
0x45 |
0XF9 |
| 0Xa8 |
0x50 |
0x3C |
0x9F |
表1.25 先转10进制
| 208 |
239 |
170 |
251 |
| 77 |
51 |
133 |
67 |
| 2 |
127 |
69 |
249 |
| 171 |
91 |
60 |
159 |
转10进制进行与固定矩阵相乘
得到结果矩阵后,将其转为16进制,到此第一轮加密结束,后续只需将结果矩阵当成第2个KEY进行执行同样的加密操作。
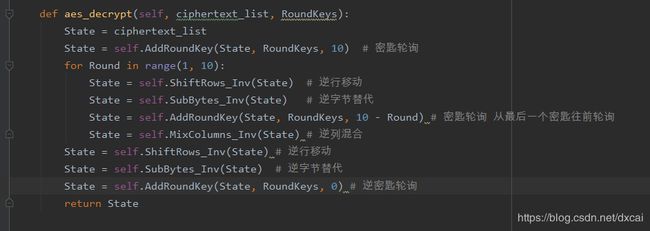
解密操作和加密操作一样,用最后一组密匙对密文进行密匙轮询,再用逆S盒进行字节替代,行移动是向右移动,列混合是乘固定矩阵的逆矩阵,后面操作与前面操作一样,轮询10次即可解密回来。
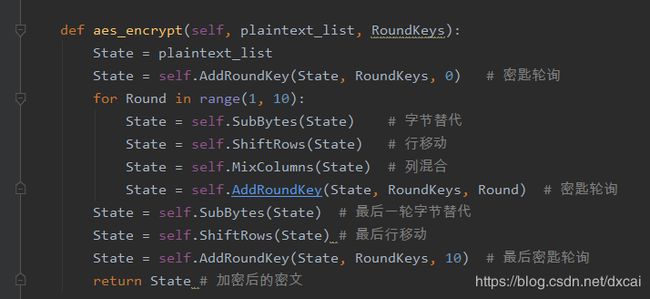
AES加密的代码实现,由于代码过多,只列出主要加密,解密代码,具体代码如图
1.2 不对称加密
不对称加密算法使用两把完全不同但又是完全匹配的一对钥匙,进行加解密,一般使用公匙加密,私匙解密,常见的加密算法有RSA,ECC,DSA加密算法。不对称加密由于其加解密耗时长,常用作小量的数据加密。第三方机构常用私密加密生成证书(只有自己公密可以认证),客户端用公密认证证书的可靠性。
1.2.1 RSA加密算法
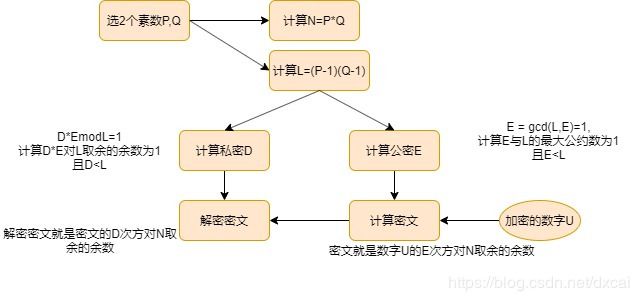
RSA算法是基于一个简单的数论事实,即将两个大的质数相乘非常容易,但是想要对其乘积进行因式分解为两个大的质数确非常困难,因此可以将乘积公开作为加密秘钥,来进行加解密,具体如图
E:公密
D:私密
N:两个pq的乘积
密文 = 明文的E次幂对N取余的余数
明文 = 密文的D次幂对N去与的余数
例如:p = 7 q = 11
求N:N = p×q = 7×11=77
求L:L = (p-1)×(q-1)=6×10=60
求E:gcd(E,L) = 1 , 1 gcd(E,60) = 1 求D:E×D mod L = 1 1 解密成功!!! 当P,Q特别特别大时,已知E求D会变的特别复杂,所以常将(E,N)做公密,(D,N)做私密 先进入一个这样的场景1和2 据Y不知不觉的就传给了小红,这里面体现的就是ECC的加密原理。如公式总结: 方法一: 每个人都会算加,减,乘,除,幂运算,有人会算log23 = x 方法二: 由于logc1G 现在定义一个有限域Fp 解释一下同余定理,同余定理是指两个数对同一个数取余得到的余数相同。例如5和3对2取余都是1那么我可以写成5≡3(mod 2),已知3(mod2)怎么求5呢? 直接3对2取余为1,所以3(mod2)=2k+1(k为整数) 例如: 椭圆曲线已知E23(1,1)上两点P(3,10),Q(9,7)求: (1) -P (2) P+Q E23(1,1) = Ep(a,b) (1) 计算-P −P=(3,−10(mod23)) 我们知道-10对23取余是-10 所以-10(mod23)=23k-10(k为整数),这里K取1,即-p=(3,13) (2)计算P+Q 由上面公式可知K = (7-10)/(9-6)(mod 23) = -(1/2)(mod23) (1/2)×(2)=1(mod23) 1(mod23)=23k+1 取k为1 得出 1/2×2= 24 即1/2 = 12 所以K = -12(mod23) = 23k-12 取k为1 即k = 11 P+Q =(x3,y3) = ((11^2-3-9)(mod23),11(3-(11^2-3-9)(mod23))-10 (mod23)) =(109(mod23),11(3-109(mod23))-10(mod23)) =(17,(11(3-17)-10)(mod23)) =(17,23k-164) k取8 =(17,20) (3)2P K = ((3×3^2+1)/(2×10))(mod23) = (7/5)(mod23) 5×1/5 = 1(mod23) 5×1/5 = 23k+1 k取3 1/5 = 14 K = 7×14(mod23) = 23k+6(k为整数) k取0 K = 6 2P = (x3,y3) =((6×6-3-3)(mod23),(6×(3-x3)-10)(mod23)) =(30(mod23),(6×(3-x3)-10)(mod23)) =(7,(-34)(mod23)) =(7,23k-34) 取k = 2 =(7,12) 是不是发现新的运算法则,利用这个运算法则去计算ECC的数据 举个栗子: 现在我们取椭圆曲线上一点作为基点G 假设选定E29(4,20),基点G(13,23) 基点G的阶数n=37,P = 29, 定义私密k = 25 (k 生成公密 G =kG =25G(mod29) =25(13,23)(mod29) =(14,6) 随机选取一个数r = 5,需要加密的数据为3,将3编码到曲线上即(3,28) C1 =M+rK =M+6K =(3,28)+6×(14,6)(mod29) =(3,28)+(27,27)(mod29) =(6,12) (加密的数据) C2 =rG =6G(mod29) =(5,7) 解密:C1−kC2 =(6,12)−25C2(mod29) =(6,12)−25×(5,7)(mod29) =(6,12)−(27,27)(mod29) =(3,28) 注意,这里的所有加减乘除,都不是直接加减乘除,就向上面的例子一样,P+Q,2P,-P的操作一样,是有个(mod29)的操作,所以每次相加出来的点都是不同的。 散列算法又有MD5和SHA加密算法,他们的原理都是将不定长的输入,输出成定长,不可逆,雪崩的数据,具体流程如图 MD5加密将不确定长度的输入,经过MD5加密后生成固定长度32位的输出: 哈希加密算法常用在文件的完整性校验,密码的正确性校验方面 对于传输少量的数据,我们优先选择RSA不对称加密算法,对称加密算法的密匙是不方便保存,另外因为数据量小,所以RSA加密消耗资源,会比较小,加解密速度方面也会比较快,使用RSA加密算法,公密公开,客户端直接用公密加密数据,服务端用私密解密数据。 对于大量数据,我们采用RSA+AES加密算法混合使用,加密大量数据,RSA不对称加密算法是不适合加密大量,加解速度慢,消耗资源多,AES加密算法加解密速度快,资源消耗的也少,这样我们可以用AES加密算法加密数据,用RSA加密算法加密密匙,这样的即保证了加密大量数据的加解密速度,也保证的密匙传输的安全性。具体的传输过程流程图 1.服务端先用RSA加密算法生成公密M,私密N 2.客户端请求服务端拿到公密M 3.客户端拿到公密M之后,随机生成一个密匙K,用于AES加密的密匙K 4.我们将大量数据进行AES加密,将密匙用RSA公密M加密 5.将加密数据和加密的密匙K一起传至服务端 6.服务端拿到加密的数据和加密的密匙K,先用私密对加密的密匙进行解密,7.拿到里面的(AES)密匙K,在用密匙K进行解密客户端传来的加密数据。 8.后面的交互就可以直接用密匙K加解密就可以了。 对于只存不取的数据我们可以用hash加密,将其加密为不可解的数据,安全性更高,对于数据库的密码,一般会用MD5加”盐”加密,在输入的字符串后面拼接一个字符串,这样是为了保证加密的安全性。 HTTPS也是一种传输协议,一种安全传输协议。主要有获取证书,认证,加解密数据三个主要过程,获取证书,证书认证,数据传输加解密 生成证书过程: 认证证书过程: 数据传输加解密: AK,SK是云主机用于验证某个发送请求的用户的身份。AK/SK是客户端与服务端都有的的密匙。 AK: Access Key Id(AK)用于标示用户 SK: Secret Access Key(SK)是用户用于加密认证字符串和云端用来验证认字符串的密钥 具体验证过程如下: 服务端: Mongo数据在最新的4.2版本退出字段加密,仅限企业版可以使用,mongo在服务端可数据库之间加了一个应用程序,根据用户需求,当应用程序检测到有需要加密的字段时,会将该字段进行加密进入数据库。同理,出数据库时会进行对应的解密 应用程序就是在服务端和数据库之间的多了的一层,他由五个部分组成:加解密程序,通信程序,KMS,JSON规则,mongo集群。 加解密程序:主要是负责加密数据和解密数据 通信程序:主要负责解析KMS,JSON规则,mongo集群,与加解密程序通信,告诉加解密程序,加密的KEY是什么,加密算法是什么等。 KMS:是一个第三方密匙管理服务,用来存储和获取密匙的地方。 JSON规则:里面主要是用户指定的加密规则,是AES加密还是DES3加密 Mongo集群:存储数据密钥密钥库的MongoDB集群。密钥保管库群集可能与存储客户端加密数据的群集不同 数据加密过程如下: 出库也是执行同样的原理,如果用户不能访问云端的key,拿到的将是没有解密过的数据。
E = 13
D = 37
明文 = 20 明文小于N
加密 2013![]() mod 77 = 69
mod 77 = 69
解密 6937![]() mod 77 = 20
mod 77 = 201.2.2 ECC加密算法
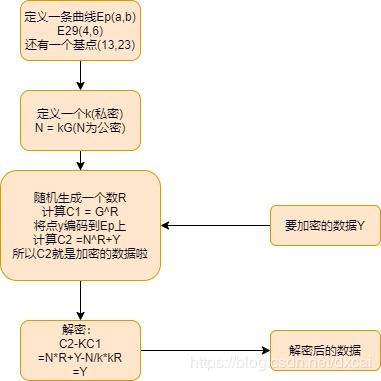
G × k = N (G,N公开,k保密,k就是传说中的密钥,N就是传说中的公钥,G一般在算法里写死了,也叫做曲线参数)
C1 = G×M
C2 = N × M + x (M随机选取,x为要加密的数字,M和x都保密)
x = c2 - C1×k
= N×M+x-G×M×k
= G×M×k - G×M×k +x
= x
方法二:
x = C2-N×M= C2 – N×(C1/G)
问题:C2,N,C1,G都是已知数,都能直接算出来,干嘛还要c2-c1*k这么复杂![]() 这类对数吗?至少特别特别难,ECC就利用这个原理来进行加解密。
这类对数吗?至少特别特别难,ECC就利用这个原理来进行加解密。
GK![]() = N
= N
C1 = GM![]()
C2 = NM![]() + X
+ X
方法一:
x = c2 - C1K![]()
= NM![]() + X - GMK
+ X - GMK![]()
=GMK![]() + X - GMK
+ X - GMK![]()
x = C2-N×M= C2 – N×(logc1G![]() )
)![]() 是一个求不出来的具体的数,所以方法二是不可取的,所以就只能使用方案一,只有知道k利用C2-kC2才能解出来。ECC就是利用这个原理进行加密,k为私密,N为公密,x为加密数据。了解ECC加密算法前,我们先了解有限域的计算方法,基本规则:
是一个求不出来的具体的数,所以方法二是不可取的,所以就只能使用方案一,只有知道k利用C2-kC2才能解出来。ECC就是利用这个原理进行加密,k为私密,N为公密,x为加密数据。了解ECC加密算法前,我们先了解有限域的计算方法,基本规则:
a. Fp中p(p为质数)个元素0,1,2,…, p-2,p-1
b. Fp的加法是a+b≡c(mod p)
c. Fp的乘法是a×b≡c(mod p)
d. Fp的除法是a÷b≡c(mod p),即 a×b^(-1)≡c (mod p),b-1也是一个0到p-1之间的整数,但满足b×b-1≡1 (mod p)
e. Fp的单位元是1,零元是 0
f. Fp域内运算满足交换律、结合律、分配律
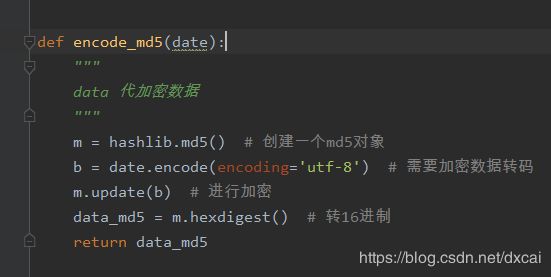
(3) 2P1.3 散列算法
传输加密
2.1 少量数据
2.2 大量数据
2.3 只存不取的数据
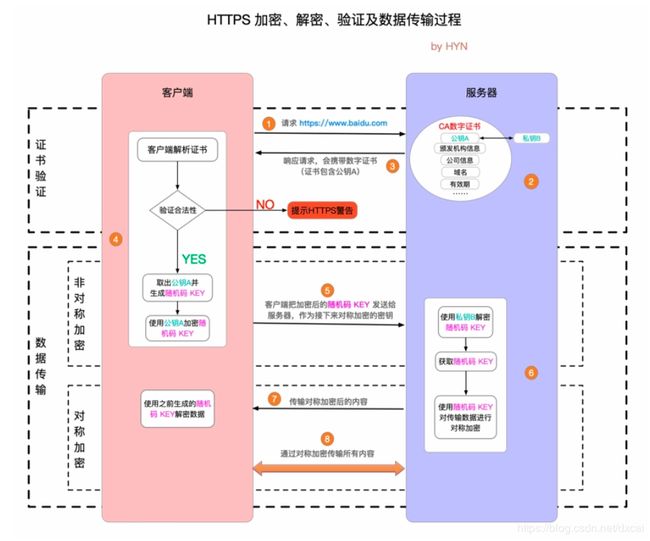
2.4 HTTPS工作原理
2.5 AK/SK认证
客户端:
3 MONGO数据库加密的方案
3.1 数据库层