冒泡排序（算法）

常见算法分类

十种常见排序算法一般分为以下几种： 
（1）非线性时间比较类排序：交换类排序（快速排序和冒泡排序）、插入类排序（简单插入排序和希尔排序）、选择类排序（简单选择排序和堆排序）、归并排序（二路归并排序和多路归并排序）；

（2）线性时间非比较类排序：计数排序、基数排序和桶排序。

总结： 
（1）在比较类排序中，归并排序号称最快，其次是快速排序和堆排序，两者不相伯仲，但是有一点需要注意，数据初始排序状态对堆排序不会产生太大的影响，而快速排序却恰恰相反。

（2）线性时间非比较类排序一般要优于非线性时间比较类排序，但前者对待排序元素的要求较为严格，比如计数排序要求待排序数的最大值不能太大，桶排序要求元素按照 hash 分桶后桶内元素的数量要均匀。线性时间非比较类排序的典型特点是以空间换时间。

交换类排序

交换排序的基本方法是：两两比较待排序记录的排序码，交换不满足顺序要求的偶对，直到全部满足位置。常见的冒泡排序和快速排序就属于交换类排序。

冒泡排序

算法思想： 
从数组中第一个数开始，依次遍历数组中的每一个数，通过相邻比较交换，每一轮循环下来找出剩余未排序数中的最大数并”冒泡”至数列的顶端。

算法步骤： 
（1）从数组中第一个数开始，依次与下一个数比较并次交换比自己小的数，直到最后一个数。如果发生交换，则继续下面的步骤，如果未发生交换，则数组有序，排序结束，此时时间复杂度为O(n)； 
（2）每一轮”冒泡”结束后，最大的数将出现在乱序数列的最后一位。重复步骤（1）。

稳定性：稳定排序。

时间复杂度： O(n)至O(n2)，平均时间复杂度为O(n2)。

最好的情况：如果待排序数据序列为正序，则一趟冒泡就可完成排序，排序码的比较次数为n-1次，且没有移动，时间复杂度为O(n)。

最坏的情况：如果待排序数据序列为逆序，则冒泡排序需要n-1次趟起泡，每趟进行n-i次排序码的比较和移动，即比较和移动次数均达到最大值： 
比较次数:Cmax=∑i=1n−1(n−i)=n(n−1)/2=O(n2) 
移动次数等于比较次数，因此最坏时间复杂度为O(n2)。

基础代码示例：

package com.bubblesort;

/**
 * 冒泡排序（针对数组）
 * 
 * @author Lenovo
 *
 */
public class Bubble {
	public void bubblesort(int array[]) {
		int count = 0; // 需要排序的次数
		// 循环的次数为数组长度减一，剩下的一个数不需要排序
		for (int i = 0; i < array.length - 1; i++) {
			// 循环次数为待排序数第一位数冒泡至最高位的比较次数
			for (int j = 0; j < array.length - i - 1; j++) {
				if (array[j] > array[j + 1]) {
					int temp = array[j + 1];
					array[j + 1] = array[j];
					array[j] = temp;
				}
				// 交换或者使用如下方式
				// a=a^b;
				// b=b^a;
				// a=a^b;
				count++;
			}
		}
		for (int i = 0; i < array.length; i++) {
			System.out.print(array[i] + "、");
		}
		System.out.println();
		System.out.println("排序总次数："+count);
	}

}

       一组不确定的数组利用冒泡排序，在时间复杂度上的开销有点过大，而对于有的数组排序也并不需要达到最大的开销就可以将排序做好，所以要做一定的优化，进行简单的优化就是在循环过程中增加一个布尔值变量作为监听作用，在每一趟的每一轮排序结束都会进行有效判断，如果当前排序已经达到排序要求，即可跳出排序工作，以节省时间。下面实例即简单优化代码：

package com.bubblesort;

/**
 * 冒泡排序（针对数组）
 * 
 * @author Lenovo
 *
 */
public class Bubble {
	public void bubblesort(int array[]) {
		int count = 0; // 需要排序的次数
		// 循环的次数为数组长度减一，剩下的一个数不需要排序
		for (int i = 0; i < array.length - 1; i++) {
			boolean tate = true; // 利用布尔变量设置，优化排序
			// 循环次数为待排序数第一位数冒泡至最高位的比较次数
			for (int j = 0; j < array.length - i - 1; j++) {
				if (array[j] > array[j + 1]) {
					int temp = array[j + 1];
					array[j + 1] = array[j];
					array[j] = temp;
					tate = false;
				}
				count++;
			}
			if (tate) {
				break;
			}
		}
		for (int i = 0; i < array.length; i++) {
			System.out.print(array[i] + "、");
		}
		System.out.println();
		System.out.println("排序总次数:"+count);
	}

}

简单测试

package com.bubblesort;

public class Test {

	public static void main(String[] args) {
		Bubble bubble = new Bubble();
		int array[] ={5,4,8,9,2,8,4,12,9,45,1,7};
		int array1[]={1,5,3,4,2,9,8};
		int array2[]={5,4,3,2,1};
		bubble.bubblesort(array);
		bubble.bubblesort(array1);
		bubble.bubblesort(array2);
	}
}

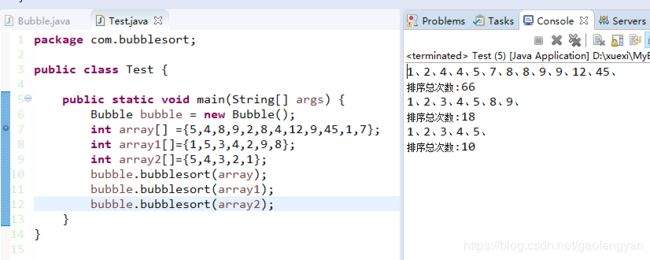
测试结果：

       从测试可以看出，array2是完全倒序，这样的排序用冒泡就必然会达到咋打复杂程度的时间；而数组array1这样的数组就可以根据数组的组合节约一定的排序时间。

       那么，除了以上的简单优化，还有没有更好的其他优化方法呢？

除此之外，在做的时候发现一个代码少，同样可以达到以上冒泡排序优化后的效果，代码如下：

package com.bubblesort;

/**
 * 冒泡排序（针对数组）
 * 
 * @author Lenovo
 *
 */
public class Bubble {
	
	public void bubblesort2(int array[]) {
		int coun = 0; // 交换次数
		int left = 0;
		int right = array.length - 1;
		long time = System.currentTimeMillis(); // 系统起始时间
		for (int i = left; i < right; i++) {
			if (array[i] > array[i + 1]) {
				int temp = array[i];
				array[i] = array[i + 1];
				array[i + 1] = temp;
				if (i != 0) {
					i -= 2;
				}
			}
			coun++;
		}
		time = System.currentTimeMillis() - time; // 排序完成后的所花时间
		System.out.println("排序所花时间：" + time);
		for (int i = 0; i < array.length; i++) {
			System.out.print(array[i] + "、");
		}
		System.out.println();
		System.out.println("自定义冒泡排序总次数:" + coun);
	}

}

在学习的时候还发一种双向定向排序法，又称为“鸡尾酒排序法”，在效率比冒泡排序更好。鸡尾酒排序，也叫定向冒泡排序，是冒泡排序的一种改进。此算法与冒泡排序的不同处在于从低到高然后从高到低，而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的效能。

package com.bubblesort;

/**
 * 冒泡排序（针对数组）
 * 
 * @author Lenovo
 *
 */
public class Bubble {

	/**
	 * 定向冒泡排序
	 * 
	 * @param array
	 */
	public void bubblesort1(int array[]) {
		int coun = 0;
		int left = 0;
		int right = array.length - 1;
		boolean flag = false;
		while (left < right / 2) { // 因为是双向排序，所以比较次数是原数组比较次数的1/2即可。
			// 将数字大的全部丢到右边
			for (int i = left; i < right; i++) {
				if (array[i] > array[i + 1]) {
					int temp = array[i];
					array[i] = array[i + 1];
					array[i + 1] = temp;
					flag = true;
				}
				// coun++;
			}
			right--; // 每当一个大的数字在右边排好后，排序数组长度自动减少一位，为下一次排序减少循环比较次数
			// 正向升序排序完成后，立即反向降序排序，将小的数字依次丢到最左边。
			for (int i = right; i > left; i--) {
				if (array[i - 1] > array[i]) {
					int temp1 = array[i - 1];
					array[i - 1] = array[i];
					array[i] = temp1;
					flag = true;
				}
				// coun++;
			}
			left++; // 每当一个小的数字在右边排好后，排序数组长度自动减少一位，为下一次排序减少循环比较次数
			if (!flag) {
				break;
			}
			coun++; // 数据交换次数
		}
		for (int i = 0; i < array.length; i++) {
			System.out.print(array[i] + "、");
		}
		System.out.println();
		System.out.println("定向冒泡排序总次数:" + coun);
	}

}

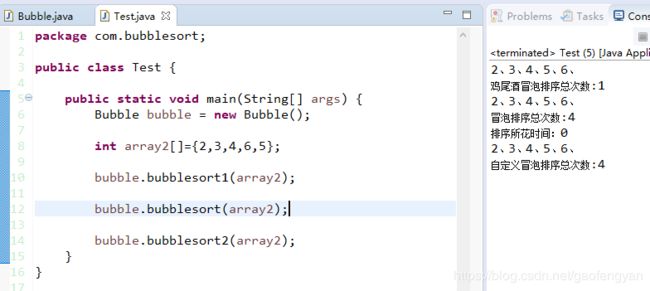
最后做一个简单的测试，结果如下：

总结：尽管冒泡排序是最容易了解和实现的排序算法之一，但它对于少数元素之外的数列排序是很没有效率的。在乱数序列的状态下，鸡尾酒排序与冒泡排序的效率都很差劲。

学习参考网址：http://www.cnblogs.com/eniac12/p/5329396.html