数据结构和算法-栈的基本实现
文章目录
- 1 使用数组实现栈
- 1.1 实现动态数组
- 1.2 动态数组的时间复杂度分析
- 1.3 复杂度震荡
- 1.4 使用数组实现栈
- 2 使用链表实现栈
- 2.1 链表的实现
- 2.2 链表的时间复杂度分析
- 2.3 使用链表实现栈
1 使用数组实现栈
1.1 实现动态数组
public class Array<E> {
private E[] data;
private int size;
// 构造函数,传入数组的容量capacity构造Array
public Array(int capacity){
data = (E[])new Object[capacity];
size = 0;
}
// 无参数的构造函数,默认数组的容量capacity=10
public Array(){
this(10);
}
// 获取数组的容量
public int getCapacity(){
return data.length;
}
// 获取数组中的元素个数
public int getSize(){
return size;
}
// 返回数组是否为空
public boolean isEmpty(){
return size == 0;
}
// 在index索引的位置插入一个新元素e
public void add(int index, E e){
if(index < 0 || index > size)
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
if(size == data.length)
resize(2 * data.length);
for(int i = size - 1; i >= index ; i --)
data[i + 1] = data[i];
data[index] = e;
size ++;
}
// 向所有元素后添加一个新元素
public void addLast(E e){
add(size, e);
}
// 在所有元素前添加一个新元素
public void addFirst(E e){
add(0, e);
}
// 获取index索引位置的元素
public E get(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Get failed. Index is illegal.");
return data[index];
}
public E getLast(){
return get(size - 1);
}
public E getFirst(){
return get(0);
}
// 修改index索引位置的元素为e
public void set(int index, E e){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Set failed. Index is illegal.");
data[index] = e;
}
// 查找数组中是否有元素e
public boolean contains(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return true;
}
return false;
}
// 查找数组中元素e所在的索引,如果不存在元素e,则返回-1
public int find(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return i;
}
return -1;
}
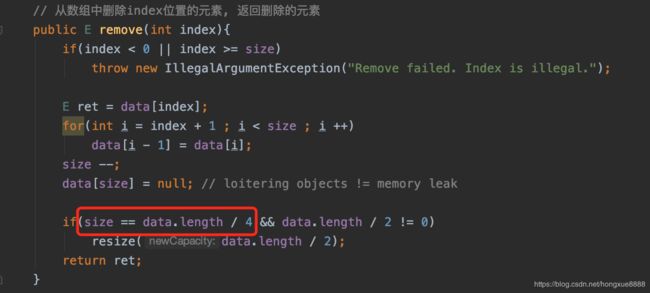
// 从数组中删除index位置的元素, 返回删除的元素
public E remove(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Remove failed. Index is illegal.");
E ret = data[index];
for(int i = index + 1 ; i < size ; i ++)
data[i - 1] = data[i];
size --;
data[size] = null; // loitering objects != memory leak
if(size == data.length / 4 && data.length / 2 != 0)
resize(data.length / 2);
return ret;
}
// 从数组中删除第一个元素, 返回删除的元素
public E removeFirst(){
return remove(0);
}
// 从数组中删除最后一个元素, 返回删除的元素
public E removeLast(){
return remove(size - 1);
}
// 从数组中删除元素e
public void removeElement(E e){
int index = find(e);
if(index != -1)
remove(index);
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
res.append('[');
for(int i = 0 ; i < size ; i ++){
res.append(data[i]);
if(i != size - 1)
res.append(", ");
}
res.append(']');
return res.toString();
}
// 将数组空间的容量变成newCapacity大小
private void resize(int newCapacity){
E[] newData = (E[])new Object[newCapacity];
for(int i = 0 ; i < size ; i ++)
newData[i] = data[i];
data = newData;
}
}
1.2 动态数组的时间复杂度分析
- 添加操作
- 删除操作
- 修改操作
- 查找操作
1.3 复杂度震荡
出现问题的原因:removeLast时resize过于着急(Eager)
解决方案:Lazy
当size == capacity / 4时,才将capacity减半
1.4 使用数组实现栈
public interface Stack<E> {
int getSize();
boolean isEmpty();
void push(E e);
E pop();
E peek();
}
public class ArrayStack<E> implements Stack<E> {
private Array<E> array;
public ArrayStack(int capacity){
array = new Array<>(capacity);
}
public ArrayStack(){
array = new Array<>();
}
@Override
public int getSize(){
return array.getSize();
}
@Override
public boolean isEmpty(){
return array.isEmpty();
}
public int getCapacity(){
return array.getCapacity();
}
@Override
public void push(E e){
array.addLast(e);
}
@Override
public E pop(){
return array.removeLast();
}
@Override
public E peek(){
return array.getLast();
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append("Stack: ");
res.append('[');
for(int i = 0 ; i < array.getSize() ; i ++){
res.append(array.get(i));
if(i != array.getSize() - 1)
res.append(", ");
}
res.append("] top");
return res.toString();
}
}
public class Main {
public static void main(String[] args) {
ArrayStack<Integer> stack = new ArrayStack<>();
for(int i = 0 ; i < 5 ; i ++){
stack.push(i);
System.out.println(stack);
}
stack.pop();
System.out.println(stack);
}
}
2 使用链表实现栈
2.1 链表的实现
public class LinkedList<E> {
private class Node{
public E e;
public Node next;
public Node(E e, Node next){
this.e = e;
this.next = next;
}
public Node(E e){
this(e, null);
}
public Node(){
this(null, null);
}
@Override
public String toString(){
return e.toString();
}
}
private Node dummyHead;
private int size;
public LinkedList(){
dummyHead = new Node();
size = 0;
}
// 获取链表中的元素个数
public int getSize(){
return size;
}
// 返回链表是否为空
public boolean isEmpty(){
return size == 0;
}
// 在链表的index(0-based)位置添加新的元素e
// 在链表中不是一个常用的操作,练习用:)
public void add(int index, E e){
if(index < 0 || index > size)
throw new IllegalArgumentException("Add failed. Illegal index.");
Node prev = dummyHead;
for(int i = 0 ; i < index ; i ++)
prev = prev.next;
prev.next = new Node(e, prev.next);
size ++;
}
// 在链表头添加新的元素e
public void addFirst(E e){
add(0, e);
}
// 在链表末尾添加新的元素e
public void addLast(E e){
add(size, e);
}
// 获得链表的第index(0-based)个位置的元素
// 在链表中不是一个常用的操作,练习用:)
public E get(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Get failed. Illegal index.");
Node cur = dummyHead.next;
for(int i = 0 ; i < index ; i ++)
cur = cur.next;
return cur.e;
}
// 获得链表的第一个元素
public E getFirst(){
return get(0);
}
// 获得链表的最后一个元素
public E getLast(){
return get(size - 1);
}
// 修改链表的第index(0-based)个位置的元素为e
// 在链表中不是一个常用的操作,练习用:)
public void set(int index, E e){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Set failed. Illegal index.");
Node cur = dummyHead.next;
for(int i = 0 ; i < index ; i ++)
cur = cur.next;
cur.e = e;
}
// 查找链表中是否有元素e
public boolean contains(E e){
Node cur = dummyHead.next;
while(cur != null){
if(cur.e.equals(e))
return true;
cur = cur.next;
}
return false;
}
// 从链表中删除index(0-based)位置的元素, 返回删除的元素
// 在链表中不是一个常用的操作,练习用:)
public E remove(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Remove failed. Index is illegal.");
Node prev = dummyHead;
for(int i = 0 ; i < index ; i ++)
prev = prev.next;
Node retNode = prev.next;
prev.next = retNode.next;
retNode.next = null;
size --;
return retNode.e;
}
// 从链表中删除第一个元素, 返回删除的元素
public E removeFirst(){
return remove(0);
}
// 从链表中删除最后一个元素, 返回删除的元素
public E removeLast(){
return remove(size - 1);
}
// 从链表中删除元素e
public void removeElement(E e){
Node prev = dummyHead;
while(prev.next != null){
if(prev.next.e.equals(e))
break;
prev = prev.next;
}
if(prev.next != null){
Node delNode = prev.next;
prev.next = delNode.next;
delNode.next = null;
size --;
}
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
Node cur = dummyHead.next;
while(cur != null){
res.append(cur + "->");
cur = cur.next;
}
res.append("NULL");
return res.toString();
}
}
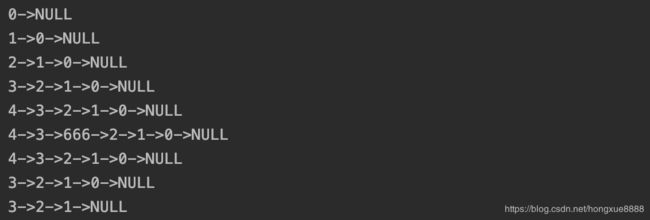
public class Main {
public static void main(String[] args) {
LinkedList<Integer> linkedList = new LinkedList<>();
for(int i = 0 ; i < 5 ; i ++){
linkedList.addFirst(i);
System.out.println(linkedList);
}
linkedList.add(2, 666);
System.out.println(linkedList);
linkedList.remove(2);
System.out.println(linkedList);
linkedList.removeFirst();
System.out.println(linkedList);
linkedList.removeLast();
System.out.println(linkedList);
}
}
2.2 链表的时间复杂度分析
2.3 使用链表实现栈
public class LinkedListStack<E> implements Stack<E> {
private LinkedList<E> list;
public LinkedListStack(){
list = new LinkedList<>();
}
@Override
public int getSize(){
return list.getSize();
}
@Override
public boolean isEmpty(){
return list.isEmpty();
}
@Override
public void push(E e){
list.addFirst(e);
}
@Override
public E pop(){
return list.removeFirst();
}
@Override
public E peek(){
return list.getFirst();
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append("Stack: top ");
res.append(list);
return res.toString();
}
public static void main(String[] args) {
LinkedListStack<Integer> stack = new LinkedListStack<>();
for(int i = 0 ; i < 5 ; i ++){
stack.push(i);
System.out.println(stack);
}
stack.pop();
System.out.println(stack);
}
}
public class Main {
// 测试使用stack运行opCount个push和pop操作所需要的时间,单位:秒
private static double testStack(Stack<Integer> stack, int opCount){
long startTime = System.nanoTime();
Random random = new Random();
for(int i = 0 ; i < opCount ; i ++)
stack.push(random.nextInt(Integer.MAX_VALUE));
for(int i = 0 ; i < opCount ; i ++)
stack.pop();
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int opCount = 100000;
ArrayStack<Integer> arrayStack = new ArrayStack<>();
double time1 = testStack(arrayStack, opCount);
System.out.println("ArrayStack, time: " + time1 + " s");
LinkedListStack<Integer> linkedListStack = new LinkedListStack<>();
double time2 = testStack(linkedListStack, opCount);
System.out.println("LinkedListStack, time: " + time2 + " s");
// 其实这个时间比较很复杂,因为LinkedListStack中包含更多的new操作
}
}