自组织神经网络SOM算法对Iris数据集进行聚类的matlab实现

SOM算法原理

SOM算法是一种将高维数据通过两层神经网络（输入层和竞争层）映射至用户定义的拓扑结构中，一般常用2D矩阵拓扑结构。下图是对SOM的形象展示：

---

所以算法一般分为以下几步：

第一：用户自定义拓扑结构，并对其中的每个节点的自身向量做随机初始化，向量长度与训练数据的维度相等。

第二：将一条训练数据输入至神经网络，节点间展开竞争，节点的自身向量与训练数据的欧式距离最短者作为获胜节点（winner unit），则该节点在此次迭代过程中拥有此训练数据（每次迭代前都要将上轮的训练数据归属结果清空，最后一轮迭代不清空作为最终结果）

第三：获胜节点以及其周边的节点的自身向量都可依照梯度下降的思想向训练数据调整。调整的幅度与学习率（随迭代次数递减）以及邻域函数（确定在获胜节点周边多大的范围内的节点可以调整自身向量以及调整力度，离获胜节点越远的邻域节点的调整幅度越小，随迭代次数递减，最终只调整获胜节点）有关。

其中，t表示迭代轮数，mi(t)表示拓扑结构中的第i个节点的初始自身向量，x(t)表示一条训练数据，α(t)表示学习率函数，hci(t)表示邻域函数其定义如下：

其中，rc表示获胜节点在拓扑结构中的位置（2D矩阵坐标），ri表示第i个节点在拓扑结构中的 位置，δ(t)表示调整的力度，随迭代次数递减。

第四：第二第三步迭代执行，直到满足迭代次数或收敛。

---

代码实现

mysom.m

由训练集，初始map，迭代次数，学习率生成新的map

function new_map = mysom(data,map,iter,learn_rate_init)
%mysom(data,map,time)
%data:训练集
%map:拓扑关系（map为结构体，含有字段units、submap、MQE；units为结构体数组，由结构体unit组成；
%unit结构体含有字段vector、qe、mqe、dataindex)
%iter:迭代次数
%learn_rate_init:学习率初始值
%new_map:数据分类拓扑结果
[data_row,~]=size(data);
[map_row,map_col]=size(map.units);%获取map的拓扑结构（2D矩形）
%获得邻域半径
if map_row>map_col
    neighbor_redius_init=map_col/2;
else
    neighbor_redius_init=map_row/2;
end
%设置学习率、邻域半径更新参数
learn_para=iter/3;%exp(-3)=0.0498已经足够小了
neighbor_para=learn_para/log(neighbor_redius_init);
%迭代开始
for i=1:iter
    learn_rate=learn_rate_init*exp(-i/learn_para);%学习率更新
    neighbor_redius=neighbor_redius_init*exp(-i/neighbor_para);%影响半径更新
    for j=1:data_row
        %1计算获胜神经元
        [win_row,win_col]=som_compare(map.units,data(j,:));
        %2添加训练数据进入获胜神经元
        map.units(win_row,win_col).dataindex=[map.units(win_row,win_col).dataindex,j];
        %3更新邻域内神经元向量
        map=som_adaption(map,win_row,win_col,data(j,:),learn_rate,neighbor_redius);
    end
    %若非最后一轮，下次迭代会将训练数据重新分配，所以将此轮分类结果清空
    if i~=iter
        for ii=1:map_row
            for jj=1:map_col
                map.units(ii,jj).dataindex=[];
            end
        end
    end
end
new_map=map;
end

som_compare.m

根据原有拓扑结构和某条训练数据，得出获胜节点的坐标。

function [ win_row,win_col ] = som_compare( units,data )
%som_compare( units,data )
%data:一条训练数据 1*n向量
%units:2维结构体数组描述map内的拓扑结构
%win_row:获胜神经元在拓扑结构中的行号
%win_col:获胜神经元在拓扑结构中的列号

[unit_row,unit_col]=size(units);
dist=zeros(unit_row,unit_col);%初始化距离矩阵
for i=1:unit_row
    for j=1:unit_col
        %计算欧式距离
        dist(i,j)=sqrt(sum(((units(i,j).vector)-data).*((units(i,j).vector)-data)));
    end
end
%寻找最小距离的坐标
[min1,minrow]=min(dist);
[~,win_col]=min(min1);
win_row=minrow(win_col);
end

som_adaption.m

根据获胜节点坐标、原有map、学习率和邻域半径对节点进行调整。

function adp_map = som_adaption( old_map,row,col,data,learn_rate,neighbor_redius )
%som_adaption( old_map,row,col,learn_rate,neighbor_redius )
%old_map:原有拓扑结构
%row:获胜神经元在原有拓扑结构中的行号
%col:获胜神经元在原有拓扑结构中的列号
%data:刚分类到获胜神经元的训练集向量
%learn_rate:本次迭代学习率
%neighbor_redius:本次迭代邻域半径
%adp_map:更新神经元向量后的新拓扑结构

[unit_row,unit_col]=size(old_map.units);
for i=1:unit_row
    for j=1:unit_col
        if i>=row-floor(neighbor_redius)&&i<=row+floor(neighbor_redius)...
                &&j>=col-floor(neighbor_redius)&&j<=col+floor(neighbor_redius)
            distance=(row-i)^2+(col-j)^2;
            old_map.units(i,j).vector=old_map.units(i,j).vector+learn_rate...
                *exp(-distance/(2*neighbor_redius^2))*(data-old_map.units(i,j).vector);
        end
    end
end
adp_map=old_map;
end

createmap.m

指定拓扑结构维度和向量长度，随机初始化一个map。

function map = createmap( unit_row,unit_col,lenOfvec )
%createmap( unit_row,unit_col,lenOfvec )
%unit_row:指定拓扑结构的行数
%unit_col:指定拓扑结构的列数
%lenOfvec:向量长度
%map:生成的map
map=struct('units',[],'submap',[],'MQE',0);
for i=1:unit_row
    for j=1:unit_col
        units(i,j)=struct('vector',rand(1,lenOfvec),'qe',0,'mqe',0,'dataindex',[]);
    end
end
map.units=units;
end

---

在Iris数据集上的实验结果

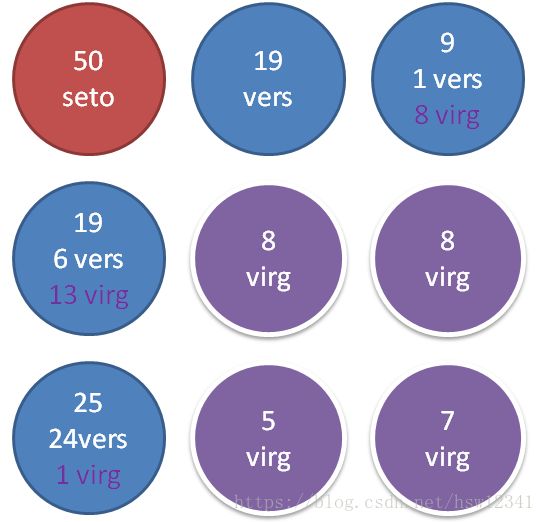
当初始化拓扑结构为3*3时，初始学习率设为0.6，迭代次数设为20时，对150条数据的聚类拓扑结果如下图：

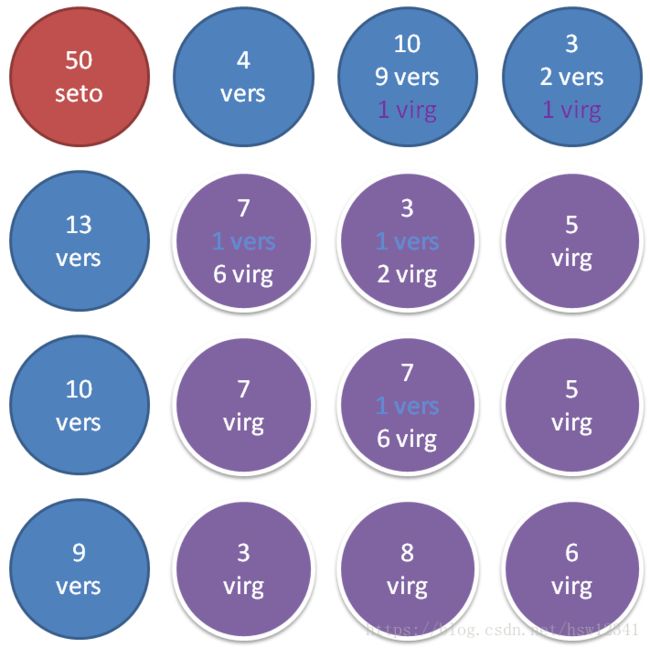
当初始化拓扑结构为4*4时，初始学习率、迭代次数不变，结果如下：

---

结论

       实现了对150条数据的拓扑展示：setosa在拓扑结构的左上角，且50条数据全部分配到一个节点中；versicolor在拓扑结构的右上行和左下列；virginica在拓扑结构的右下区域。可以从上图中看出versicolor与virginica区域有所交叉，但随着拓扑结构的增大，交叉数据数量减少。在3*3中共交叉22条数据，在4*4中交叉5条数据。

       以上是个人观察实验结果得出的一些结论，当然代码还存在可优化可修改的地方，比如学习率的初始值及递减公式和邻域半径的衰减公式都可根据实际情况而定义。总体上som算法的对于发现数据内固有的拓扑结构有很好的效果！