干货 | 季节性的分析才不简单，小心不要在随机数据中也分析出季节性

最近有人找我帮忙，具体是要某个时间序列中的「季节性」程度如何。听起来仿佛很轻松的样子，对吧？要知道在 Python 的模块包 statsmodels 中就有一个看起来很好用的 seasal_decompose 函数，并且你能在谷歌上很轻易的找到它！但实际上，这事儿却比我预期的要复杂点儿。在这篇文章中，我将分享我在处理这个项目时遇到的一些问题以及我是如何应对的。

在试图找到那些能够量化时间序列受季节性因素影响程度的帖子或论文时，我将遇到的所有例子分为两大类：

• 给出了几行代码，可以生成时间序列分解的可视化。

• 给出了如何移除时间序列中的季节性成分，从而在构建预测模型之前可以先拥有一个稳定的时间序列。

此外，每个例子都以「这是一个季节性趋势的时间序列」开头。所以，当你想去确定一个特定时间序列，它的季节性因素有多大时，这就提供不了什么帮助。

我发现没有任何人写过如何量化时间序列受季节性因素影响的程度。甚至，我还发现了一些与季节指数相矛盾的信息，于是决定继续探索下去。当然了，如果说我继续去寻找这样的信息，我想我最终也能找到些什么。但我偏不继续找，而是决定自己动手进行实验!

系列分解

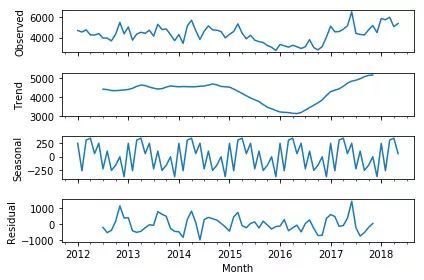
首先，我将时间序列分解为趋势，季节性和噪声成分。这些成分看起来像这个样子。 

这个时间序列有多季节性？¯\ _（ツ）_ /¯ （自上到下：观测数据，趋势分量，季节性分量，残差）

从季节分解分量的周期性来看，乍一看，数据明显是季节性的。但是，在谷歌搜索季节性分解的几个例子中，我遇到的每个季节性成分都显示出周期性。

所以，我制作了一个 0 到 1000 之间随机数据点组成的时间序列，并对其进行了分解。分解以后看起来像这样。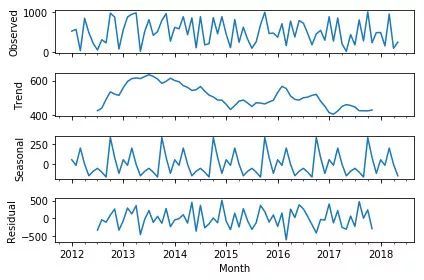

神圣的周期，蝙蝠侠！

它竟然也显示出了周期性！不过，如果仔细查看每个成分中的 y 轴，就能注意到噪声成分在随机时间序列中具有最大范围。

不过，在所讨论的时间序列中，季节性成分的范围比趋势或噪声显然要小得多。

• 趋势范围：2000（3000至5000）

• 季节范围：500（-250至250）

• 噪声范围：2000（-1000至1000）

（我注意到这里的趋势和噪声范围有相同的幅度，但却不知道这意味着什么。如果你知道的话，请毫不吝啬的在评论中分享给我们吧！）

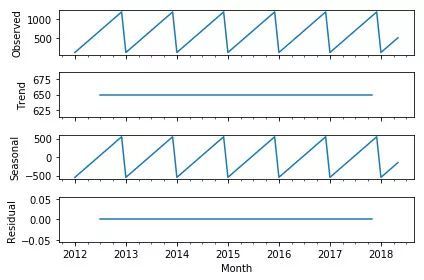
接下来，出于好玩的目的，这里还做了一个完全季节性时间序列的分解。其每年 1 月的值为 100，每月增加 100，直到 12 月达到 1200，并在 1 月再次回落到 100。

纯季节性时间序列。也说得过去吧。

正如你在纯粹由季节性趋势驱动的数据中所预期的那样，趋势和噪声分量是一个常量值0。

考虑到我们的系列看起来更接近随机数据，而不是纯粹的季节性数据，季节性分解如果说会有结果的话，那它似乎将指向一个弱季节性。在此，我对这个结论持怀疑态度，于是决定寻找更多的证据。那么接下来我们就开始使用另一种方法吧!

去趋势算法

这是一个消除趋势依赖的过程，这种依赖可能在时间序列中出现。我使用差分方法来检查数据的趋势依赖性。

假设你有一个数据集，它具有很强的年度季节性趋势。比如：如果你想预测 6 月的价值是多少，看看去年 6 月的价值，你就会得到关于你能预期的信息。

再假设你有一个趋势，它不以周期性的方式波动，而只是增加或减少。这种情况下，如果你想预测自己 6 月份的销售额，就可以通过查看 6 月份之前的月份来获得比只查看去年同期更多的信息。

这两种趋势都可以从时间序列中剔除。在差分中，你基本上是减去最相关的先前值来考虑趋势。

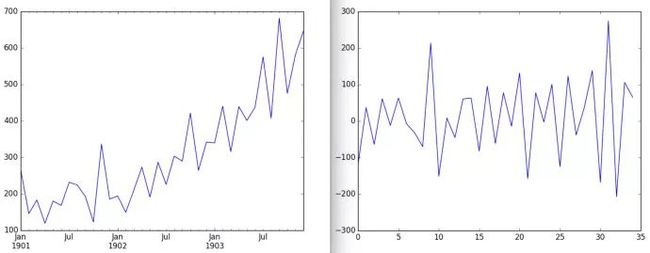
例如，从时间序列中删除一个「向右上方」的趋势，本质上就是将图形在平面上旋转，留下「向右走」，但消掉「向上走」。「去除季节性趋势基本上可以消除图表中的起伏。」时间序列的去趋势通常用于生成一个固定序列，从中可以建立一个预测模型。下面就是从数据集中移除向上向右的趋势的例子。 

之前和之后：稳定时间序列

因此，我推断，通过移除特定类型的趋势，并将结果序列与原始序列进行比较，我们可以判断特定序列对原始时间序列的「影响」程度。

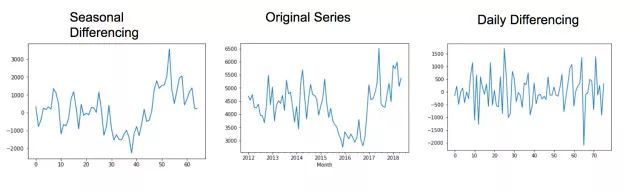
下面是每个不同的过程如何影响序列。这其中包含了原始序列的一个图作为参考。 

去趋势结果的比较

从这些数据来看，除去每日趋势(或者如上文所说仅仅是趋势组成部分)对原始系列的影响比除去季节性趋势更大。不过，去除季节性趋势也有一些影响。这巩固了我之前的结论;如果数据中有季节性因素，那么与整体趋势相比就显得很弱。

对我而言，这似乎还不足以佐证，所以我又检查了一件事。

自相关函数

在那个周末，我正喝着每月一售的数学啤酒(是的!就是有这么个东西！)，我在研究生院的一个朋友建议我研究自相关函数(ACF)。

自相关函数显示了数据集与自身随着时间的推移而变化的版本的关联程度。它计算了许多可能的时间变化的相关性（称为滞后），和表面重复的相关性模式。

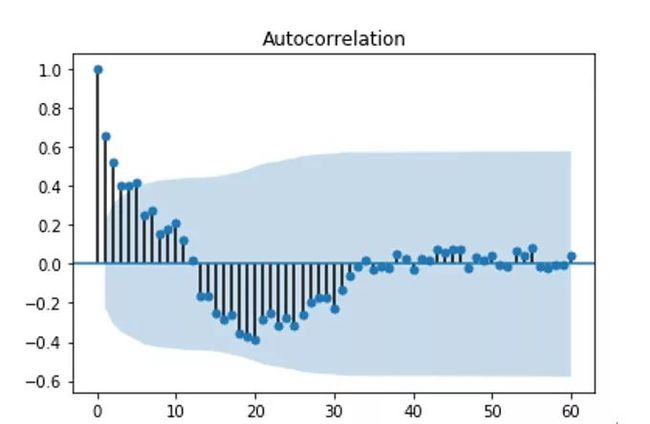
回到我们制作的数据集，我们纯季节性时间序列的 ACF 看起来像这样。

 

ACF非常季节性的时间序列

注意每隔 12 秒出现的尖峰。这意味着，当该变化是 12 个时间段(在我们的例子中是几个月)的倍数时，原始序列和其移位版本之间的相关性最高，表明了每年的季节性趋势。

这些图中的蓝色区域表示这些相关度量的置信区间。因此落在这个锥体之外的尖刺不太可能是偶然的。

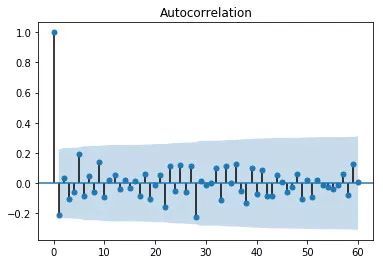
牢记这一点之后，再让我们看看随机级数的ACF。

随机生成的时间序列的ACF

在这里，有一些尖峰，但它们都非常牢固地在锥体内，所以这个ACF不支持季节性趋势的存在。

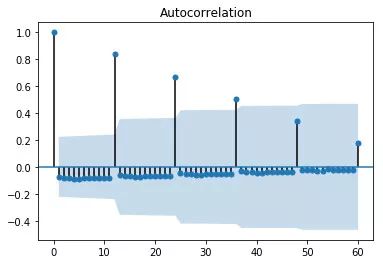
这是我们时间序列的 ACF。 

我们时间系列的ACF

这里，我们看到一些类似尖峰的区域，但是其余大多数都在圆锥体内。圆锥体外的尖峰指的是比12小得多的间隔，也就是说，当你把数据从它自身移得更远时，相关性就会降低。在我看来，时间序列的总体趋势比季节趋势对时间序列的影响要大得多。

所以，长话短说，（不好意思，其实说来话长！）我并没有找到压倒性的证据来表明，季节性在我们的序列中扮演了很重要的角色。但尽管我什么也没发现(生活可不就是这样么？让我们勇敢对面这个屡战屡败的事实呗~)，我还是认为这是一个非常有意思的分析。你也会常干这种类似的事情吗?

via：

investigating-seasonality-in-a-time-series-a-mystery-in-three-parts

转自：AI研习社

∞∞∞∞∞

公众号回复“IT派”，

邀你加入 IT派 { 深广创投圈 }