目标检测训练时候的不平衡问题
目标检测训练时候的不平衡问题
先放大佬链接(https://mp.weixin.qq.com/s/K1HTRjSLAM8mME4g1eNHtA)
当前主流的物体检测算法,如Faster RCNN和SSD等,都是将目标检测当做分类问题来考虑,即先使用先验框或者RPN等生成感兴趣的区域,再对该区域进行分类与回归位置。这种基于分类思想的目标检测算法存在样本不平衡的问题,因而会降低模型的训练效率与检测精度。
当前基于深度学习的目标检测主要包括:基于two-stage的目标检测和基于one-stage的目标检测。two-stage的目标检测框架一般检测精度相对较高,但检测速度慢;而one-stage的目标检测速度相对较快,但是检测精度相对较低。one-stage的精度不如two-stage的精度,一个主要的原因是训练过程中样本极度不均衡造成的。
定义
样本不均衡问题:指在训练的时候各个类别的样本数量不均衡,由于检测算法各不相同,以及数据集之间的差异,可能会存在正负样本、难易样本、类别间样本这3种不均衡问题。一般在目标检测任务框架中,保持正负样本的比例为1:3(经验值)。
样本不平衡实际上是一种非常常见的现象。比如:在欺诈交易检测,欺诈交易的订单应该是占总交易数量极少部分;工厂中产品质量检测问题,合格产品的数量应该是远大于不合格产品的;信用卡的征信问题中往往就是正样本居多。
目标检测任务中,样本包括哪些类别
1、正样本:标签区域内的图像区域,即目标图像块
2、负样本:标签区域以外的图像区域,即图像背景区域
3、易分正样本:容易正确分类的正样本,在实际训练过程中,该类占总体样本的比重非常高,单个样本的损失函数较小,但是累计的损失函数会主导损失函数
4、易分负样本:容易正确分类的负样本,在实际训练过程中,该类占的比重非常高,单个样本的损失函数较小,但是累计的损失函数会主导损失函数
5、难分正样本:错分成负样本的正样本,这部分样本在训练过程中单个样本的损失函数较高,但是该类占总体样本的比例较小
6、难分负样本:错分成正样本的负样本,这部分样本在训练过程中单个样本的损失函数较高,但是该类占总体样本的比例较小
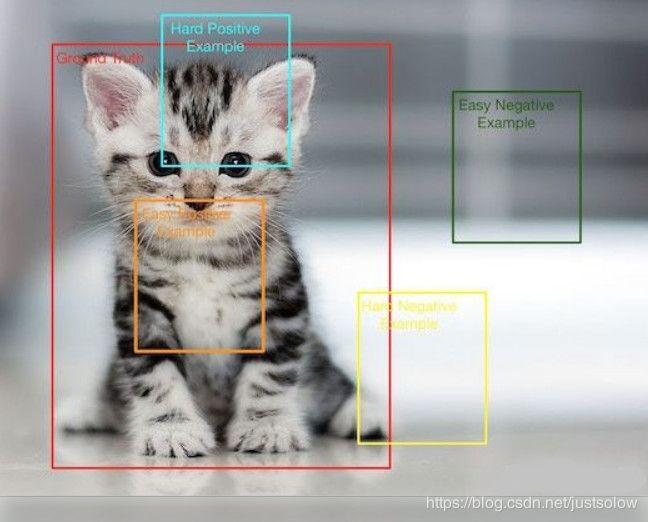
1.正负样本不均衡
以Faster RCNN为例,在RPN部分会生成20000个左右的Anchor,由于一张图中通常有10个左右的物体,导致可能只有100个左右的Anchor会是正样本,正负样本比例约为1∶200,存在严重的不均衡。
对于目标检测算法,主要需要关注的是对应着真实物体的正样本,在训练时会根据其loss来调整网络参数。相比之下,负样本对应着图像的背景,如果有大量的负样本参与训练,则会淹没正样本的损失,从而降低网络收敛的效率与检测精度。
2.难易样本不均衡
难样本指的是分类不太明确的边框,处在前景与背景的过渡区域上,在网络训练中难样本损失会较大,也是我们希望模型去学习优化的样本,利用这部分训练可以提升检测的准确率。
然而,大量的样本并非处在前景与背景的过渡区,而是与真实物体没有重叠区域的负样本,或者与真实物体重叠程度很高的正样本,这部分被称为简单样本,单个损失会较小,对参数收敛的作用有限。
虽然简单样本单个损失小,但由于数量众多,因此如果全都计算损失的话,其损失也会比难样本大很多,这种难易样本的不均衡也会影响模型的收敛与精度。
值得注意的是,由于负样本中大量的是简单样本,导致难易样本与正负样本这两个不均衡问题有一定的重叠,解决方法往往能同时对这两个问题起作用。
3.类别间样本不均衡
在有些目标检测的数据集中,还会存在类别间的不均衡问题。举个例子,数据集中有100万个车辆、1000个行人的实例标签,样本比例为1000∶1,属于典型的类别不均衡。
这种情况下,如果不做任何处理,使用该数据集进行训练,由于行人这一类别可参考标签太少,会使得模型主要关注车这一类别的检测,网络中的参数主要根据车辆的损失进行优化,导致行人的检测精度大大下降。
目前,解决样本不均衡问题的一些思路:
机器学习中,解决样本不均衡问题主要有2种思路:数据角度和算法角度。从数据角度出发,有扩大数据集、数据类别均衡采样等方法。在算法层面,目标检测方法使用的方法主要有:
Faster RCNN、SSD等算法在正负样本的筛选时,根据样本与真实物体的IoU大小,设置了3∶1的正负样本比例,这一点缓解了正负样本的不均衡,同时也对难易样本不均衡起到了作用。
Faster RCNN在RPN模块中,通过前景得分排序筛选出了2000个左右的候选框,这也会将大量的负样本与简单样本过滤掉,缓解了前两个不均衡问题。
权重惩罚:对于难易样本与类别间的不均衡,可以增大难样本与少类别的损失权重,从而增大模型对这些样本的惩罚,缓解不均衡问题。
数据增强:从数据侧入手,可以在当前数据集上使用随机生成和添加扰动的方法,也可以利用网络爬虫数据等增加数据集的丰富性,从而缓解难易样本和类别间样本等不均衡问题,可以参考SSD的数据增强方法。
近年来,不少的研究者针对样本不均衡问题进行了深入研究,比较典型的有OHEM(在线困难样本挖掘)、S-OHEM、Focal Loss、GHM(梯度均衡化)。下面将详细介绍:
1 OHEM:在线难例挖掘
OHEM算法(online hard example miniing,发表于2016年的CVPR)主要是针对训练过程中的困难样本自动选择,其核心思想是根据输入样本的损失进行筛选,筛选出困难样本(即对分类和检测影响较大的样本),然后将筛选得到的这些样本应用在随机梯度下降中训练。
传统的Fast RCNN系列算法在正负样本选择的时候采用当前RoI与真实物体的IoU阈值比较的方法,这样容易忽略一些较为重要的难负样本,并且固定了正、负样本的比例与最大数量,显然不是最优的选择。以此为出发点,OHEM将交替训练与SGD优化方法进行了结合,在每张图片的RoI中选择了较难的样本,实现了在线的难样本挖掘。

OHEM实现在线难样本挖掘的网络如上图所示。图中包含了两个相同的RCNN网络,上半部的a部分是只可读的网络,只进行前向运算;下半部的b网络即可读也可写,需要完成前向计算与反向传播。
在一个batch的训练中,基于Fast RCNN的OHEM算法可以分为以下5步:
(1)按照原始Fast RCNN算法,经过卷积提取网络与RoI Pooling得到了每一张图像的RoI。
(2)上半部的a网络对所有的RoI进行前向计算,得到每一个RoI的损失。
(3)对RoI的损失进行排序,进行一步NMS操作,以去除掉重叠严重的RoI,并在筛选后的RoI中选择出固定数量损失较大的部分,作为难样本。
(4)将筛选出的难样本输入到可读写的b网络中,进行前向计算,得到损失。
(5)利用b网络得到的反向传播更新网络,并将更新后的参数与上半部的a网络同步(这里不太明白,怎么同步???共享权重吗?),完成一次迭代。
当然,为了实现方便,OHEM的简单实现可以是:在原有的Fast-RCNN里的loss layer里面对所有的props计算其loss,根据loss对其进行排序,选出K个hard examples,反向传播时,只对这K个props的梯度/残差回传,而其他的props的梯度/残差设为0。
但是,由于其特殊的损失计算方式,把简单的样本都舍弃了,导致模型无法提升对于简单样本的检测精度,这也是OHEM方法的一个弊端。
优点:
- 对于数据的类别不平衡问题不需要采用设置正负样本比例的方式来解决,这种在线选择方式针对性更强;
2) 随着数据集的增大,算法的提升更加明显;
缺点:
只保留loss较高的样本,完全忽略简单的样本,这本质上是改变了训练时的输入分布(仅包含困难样本),这会导致模型在学习的时候失去对简单样本的判别能力。
- S-OHEM:基于loss分布采样的在线困难样本挖掘
在OHEM中定义的多任务损失函数(包括分类损失 和定位损失 ),在整个训练过程中各类损失具有相同的权重,这种方法忽略了训练过程中不同损失类型的影响,例如在训练期的后期,定位损失更为重要,因此OHEM缺乏对定位精度的足够关注。
S-OHEM算法采用了分层抽样的方法,根据loss的分布抽样训练样本。它的做法是:
首先将预设loss的四个分段:
![]()
给定一个batch,先生成输入batch中所有图像的候选RoI,再将这些RoI送入到Read only RoI网络得到RoIs的损失,然后将每个RoI计算损失并划分到上面四个分段中,然后针对每个分段,通过排序筛选困难样本.再将经过筛选的RoIs送入反向传播,用于更新网络参数。
网络中损失是一个组合,具体公式为 , 随着训练阶段变化而变化)之所以采用这个公式是因为在训练初期阶段,分类损失占主导作用;在训练后期阶段,边框回归损失函数占主导作用。
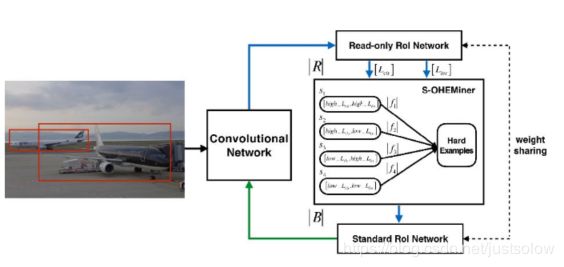
S-OHEM是基于OHEM的改进,如上图所示。网络分成两个部分:ConvNet和RoINet。RoINet又可看成两部分:Read-only RoI Network和Standard RoI Network。图中R表示向前传播的RoI的数量,B表示被馈送到反向传播的子采样的RoI的数量。S-OHEMiner根据当前训练阶段的采样分布对region proposals进行抽样。Read-only RoI Network只有forward操作,Standard RoI Network包括forward和backward操作,以hard example作为输入,计算损失并回传梯度。
RoINet的两部分共享权重,可实现高效地分配内存。在图中,蓝色箭头表示向前传播的过程,绿色箭头表示反向传播过程。
优点:
相比原生OHEM,S-OHEM考虑了基于不同损失函数的分布来抽样选择困难样本,避免了仅使用高损失的样本来更新模型参数。
缺点:
因为不同阶段,分类损失和定位损失的贡献不同,所以选择损失中的两个参数 α , β \alpha, \beta α,β需要根据不同训练阶段进行改变,当应用与不同数据集时,参数的选取也是不一样的。即引入了额外的超参数。
3 Focal loss:专注难样本
当前一阶的物体检测算法,如SSD和YOLO等虽然实现了实时的速度,但精度始终无法与两阶的Faster RCNN相比。是什么阻碍了一阶算法的高精度呢?何凯明等人将其归咎于正、负样本的不均衡,并基于此提出了新的损失函数Focal Loss及网络结构RetinaNet,在与同期一阶网络速度相同的前提下,其检测精度比同期最优的二阶网络还要高。
对于SSD等一阶网络,由于其需要直接从所有的预选框中进行筛选,即使使用了固定正、负样本比例的方法,仍然效率低下,简单的负样本仍然占据主要地位,导致其精度不如两阶网络。为了解决一阶网络中样本的不均衡问题,何凯明等人首先改善了分类过程中的交叉熵函数,提出了可以动态调整权重的Focal Loss。
1.标准交叉熵损失
首先回顾一下标准的交叉熵(Cross Entropy, CE)函数,其形式如下式所示。
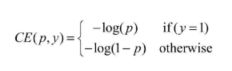
公式中,p代表样本在该类别的预测概率,y代表样本标签。可以看出,当标签为1时,p越接近1,则损失越小;标签为0时p越接近0,则损失越小,符合优化的方向。
为了方便表示,按照上式将p标记为pt:
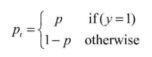
则交叉熵可以表示为下式的形式:
![]()
可以看出,标准的交叉熵中所有样本的权重都是相同的,因此如果正、负样本不均衡,大量简单的负样本会占据主导地位,少量的难样本与正样本会起不到作用,导致精度变差。
2.平衡交叉熵损失
为了改善样本的不平衡问题,平衡交叉熵在标准的基础上增加了一个系数αt来平衡正、负样本的权重,αt由超参α按照下式计算得来,α取值在[0,1]区间内。
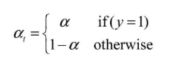
尽管平衡交叉熵损失改善了正、负样本间的不平衡,但由于其缺乏对难易样本的区分,因此没有办法控制难易样本之间的不均衡。
- 专注难样本Focal loss
Focal Loss为了同时调节正、负样本与难易样本,提出了如下所示的损失函数。
![]()
其中 用于控制正负样本的权重,当其取比较小的值来降低负样本(多的那类样本)的权重; 用于控制难易样本的权重,目的是通过减少易分样本的权重,从而使得模型在训练的时候更加专注难分样本的学习。文中通过批量实验统计得到当 时效果最好。
可以看出,对于Focal loss损失函数,有如下3个属性:
与平衡交叉熵类似,引入了αt权重,为了改善正负样本的不均衡,可以提升一些精度。
( 1 − p t ) γ \left(1-p_{t}\right)^{\gamma} (1−pt)γ是为了调节难易样本的权重。当一个边框被误分类时,pt较小,则 ( 1 − p t ) γ \left(1-p_{t}\right)^{\gamma} (1−pt)γ接近于1,其损失几乎不受影响;当pt接近于1时,表明其分类预测较好,是简单样本, ( 1 − p t ) γ \left(1-p_{t}\right)^{\gamma} (1−pt)γ接近于0,因此其损失被调低了。
γ是一个调制因子,γ越大,简单样本损失的贡献会越低。
为了验证Focal Loss的效果,何凯明等人还提出了一个一阶物体检测结构RetinaNet,其结构如下图所示。
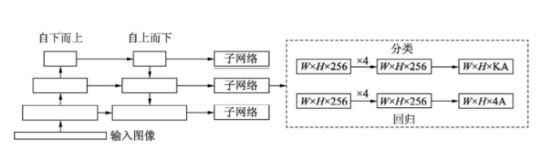
对于RetinaNet的网络结构,有以下5个细节(有时间的话会详细写一下这个网络):
(1)在Backbone部分,RetinaNet利用ResNet与FPN构建了一个多尺度特征的特征金字塔。
(2)RetinaNet使用了类似于Anchor的预选框,在每一个金字塔层,使用了9个大小不同的预选框。
(3)分类子网络:分类子网络为每一个预选框预测其类别,因此其输出特征大小为KA×W×H, A默认为9, K代表类别数。中间使用全卷积网络与ReLU激活函数,最后利用Sigmoid函数输出预测值。
(4)回归子网络:回归子网络与分类子网络平行,预测每一个预选框的偏移量,最终输出特征大小为4A×W×W。与当前主流工作不同的是,两个子网络没有权重的共享。
(5)Focal Loss:与OHEM等方法不同,Focal Loss在训练时作用到所有的预选框上。对于两个超参数,通常来讲,当γ增大时,α应当适当减小。实验中γ取2、α取0.25时效果最好。
4 GHM:损失函数梯度均衡化机制
前面讲到的OHEM算法和Focal loss各有利弊:
1、OHEM算法会丢弃loss比较低的样本,使得这些样本无法被学习到。
2、FocalLoss则是对正负样本进行加权,使得全部的样本可以得到学习,容易分类的负样本赋予低权值,hard examples赋予高权值。但是在所有的anchor examples中,出了大量的易分类的负样本外,还存在很多的outlier,FocalLoss对这些outlier并没有相关策略处理。并且FocalLoss存在两个超参,根据不同的数据集,调试两个超参需要大量的实验,一旦确定参数无法改变,不能根据数据的分布动态的调整。
GHM主要思想
GHM做法则是从样本的梯度范数出发,通过梯度范数所占的样本比例,对样本进行动态的加权,使得具有小梯度的容易分类的样本降权,具有中梯度的hard expamle升权,具有大梯度的outlier降权。
损失函数的权重(梯度密度的倒数)
就是把梯度幅值范围(X轴)划分为M个区域,对于落在每个区域样本的权重采取相同的修正方式,类似于直方图。具体推导公式如下所示。
X轴的梯度分为M个区域,每个区域长度即为 r j r_{j} rj ,第j个区域范围即为 R j R_{j} Rj ,用 ind ( g ) (g) (g) 表示落在第j个区域内的样本数量。定义ind(g)表示梯度为g的样本所落区域的序号,那么即可得出新的参数 。由于样本的梯度密度是训练时根据batch计算出来的,通常情况下batch较小,直接计算出来的梯度密度可能不稳定,所以采用滑动平均的方式处理梯度计算。
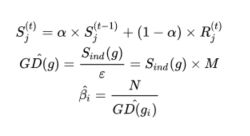
根据GHM-C的计算公式可以看出,候选样本的中的简单负样本和非常困难的异常样本(离群点)的权重都会被降低,即loss会被降低,对于模型训练的影响也会被大大减少,正常困难样本的权重得到提升,这样模型就会更加专注于那些更有效的正常困难样本,以提升模型的性能。
GHM-R边框回归损失函数
对于回归损失函数,由于原生的Smooth L1损失函数的导数为1时,样本之间就没有难易区分度了,这样的统计明显不合理.论文修改了损失函数 A S L 1 ( d ) = d 2 + μ 2 − μ A S L 1(d)=\sqrt{d^{2}+\mu^{2}}-\mu ASL1(d)=d2+μ2−μ ,梯度密度中的梯度模长是基于修改后的损失函数ASL1的导数进行计算的,GHM-R公式如下:
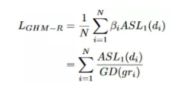
因为GHM-C和GHM-R是定义的损失函数,因此可以非常方便的嵌入到很多目标检测方法中,论文作者以focal loss(大概是以RetinaNet作为baseline),对交叉熵,focal loss和GHM-C做了对比,发现GHM-C在focal loss 的基础上在AP上提升了0.2个百分点。
具体细节可参考论文原文《Gradient Harmonized Single-stage Detector》。
总结
OHEM系列的困难样本挖掘方法在当前的目标检测框架上还是被大量地使用,在一些文本检测方法中还是被经常使用;
OHEM是针对现有样本并根据损失loss进行困难样本挖掘,Focal Loss和GHM则从损失函数本身进行困难样本挖掘;
相比Focal loss,GHM是一个动态的损失函数,即随着不同数据的分布进行变换,不需要额外的超参数调整(但是这里其实还是会涉及到一个参数,就是Unit region的数量);此外GHM在降低易分样本权重的同时,对outliner也会有一定程度的降权;
无论是Focal Loss,还是基于GHM的损失函数都可以嵌入到现有的目标检测框架中;Focal Loss只针对分类损失,而GHM对分类损失和边框损失都可以;
GHM方法在源码实现上,作者采用平均滑动的方式来计算梯度密度,不过与论文中有一个区别是在计算梯度密度的时候,没有乘以M,而是乘以有效的(也就是说有梯度信息的区间)bin个数;
之前尝试过Focal Loss用于多分类任务中,发现在精度并没有提升;但是我试过将训练数据按照训练数据的原始分布并将其引入到交叉熵函数中,准确率提升了;GHM方法的本质也是在改变训练数据的分布(将难易样本拉匀),但是到底什么的数据分布是最优的,目前尚未定论。