DP - 状态机模型 - LeetCode - 股票买卖 IV + V
DP - 状态机模型 - LeetCode - 股票买卖 IV + V
文章目录
- DP - 状态机模型 - LeetCode - 股票买卖 IV + V
- 1、股票买卖 IV
- 2、股票买卖 V
1、股票买卖 IV
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润,你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。一次买入卖出合为一笔交易。
输入格式
第一行包含整数 N 和 k,表示数组的长度以及你可以完成的最大交易数量。
第二行包含 N 个不超过 10000 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105,
1≤k≤100
输入样例1:
3 2
2 4 1
输出样例1:
2
输入样例2:
6 2
3 2 6 5 0 3
输出样例2:
7
样例解释
样例1:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
样例2:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。共计利润 4+3 = 7
分析:
有 次 数 限 制 的 股 票 买 卖 问 题 。 当 次 数 k > = n 2 时 , 就 可 以 从 贪 心 的 角 度 考 虑 — — 有次数限制的股票买卖问题。当次数k>=\frac{n}{2}时,就可以从贪心的角度考虑—— 有次数限制的股票买卖问题。当次数k>=2n时,就可以从贪心的角度考虑——《股票买卖 II》。
本 题 从 状 态 机 的 角 度 考 虑 。 本题从状态机的角度考虑。 本题从状态机的角度考虑。
f [ i , j , k ] : 表 示 考 虑 前 i 天 股 票 , 且 进 行 了 j 次 买 入 操 作 , 当 前 状 态 是 k 的 最 大 收 益 。 f[i,j,k]:表示考虑前i天股票,且进行了j次买入操作,当前状态是k的最大收益。 f[i,j,k]:表示考虑前i天股票,且进行了j次买入操作,当前状态是k的最大收益。
k = 0 o r 1 。 0 : 表 示 当 前 手 上 无 股 票 ; 1 : 表 示 当 前 手 上 有 股 票 。 k=0\ or\ 1。\\0:表示当前手上无股票;\ 1:表示当前手上有股票。 k=0 or 1。0:表示当前手上无股票; 1:表示当前手上有股票。
共 有 两 种 状 态 , 四 种 转 移 的 可 能 。 共有两种状态,四种转移的可能。 共有两种状态,四种转移的可能。
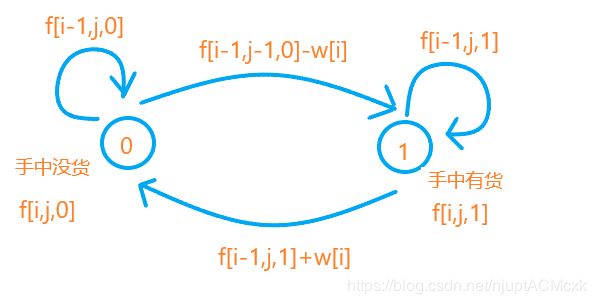
当 k = 0 时 , 当 前 手 上 无 股 票 ① 、 可 能 前 一 天 手 上 就 没 股 票 , 今 天 也 不 买 , f [ i , j , 0 ] = f [ i − 1 , j , 0 ] 。 ② 、 前 一 天 手 上 有 股 票 , 今 天 把 它 卖 了 , f [ i , j , 0 ] = f [ i − 1 , j , 1 ] + w [ i ] 。 当k=0时,当前手上无股票\\①、可能前一天手上就没股票,今天也不买,f[i,j,0]=f[i-1,j,0]。\\②、前一天手上有股票,今天把它卖了,f[i,j,0]=f[i-1,j,1]+w[i]。 当k=0时,当前手上无股票①、可能前一天手上就没股票,今天也不买,f[i,j,0]=f[i−1,j,0]。②、前一天手上有股票,今天把它卖了,f[i,j,0]=f[i−1,j,1]+w[i]。
注 意 , 这 里 我 们 定 义 j 为 已 进 行 的 买 入 操 作 次 数 , 所 以 卖 出 股 票 时 j 不 会 增 加 1 次 , 因 此 ② 中 不 是 由 f [ i − 1 , j − 1 , 1 ] 转 移 而 来 的 。 注意,这里我们定义j为已进行的买入操作次数,所以卖出股票时j不会增加1次,\\因此②中不是由f[i-1,j-1,1]转移而来的。 注意,这里我们定义j为已进行的买入操作次数,所以卖出股票时j不会增加1次,因此②中不是由f[i−1,j−1,1]转移而来的。
当 k = 1 时 , 当 前 手 上 由 股 票 ① 、 可 能 前 一 天 手 上 就 有 股 票 , 今 天 也 不 卖 , f [ i , j , 1 ] = f [ i − 1 , j , 1 ] 。 ② 、 前 一 天 手 上 没 股 票 , 今 天 买 入 股 票 , f [ i , j , 1 ] = f [ i − 1 , j − 1 , 0 ] − w [ i ] 。 当k=1时,当前手上由股票\\①、可能前一天手上就有股票,今天也不卖,f[i,j,1]=f[i-1,j,1]。\\②、前一天手上没股票,今天买入股票,f[i,j,1]=f[i-1,j-1,0]-w[i]。 当k=1时,当前手上由股票①、可能前一天手上就有股票,今天也不卖,f[i,j,1]=f[i−1,j,1]。②、前一天手上没股票,今天买入股票,f[i,j,1]=f[i−1,j−1,0]−w[i]。
每 种 状 态 转 移 时 , 分 别 在 两 种 情 况 里 取 一 个 较 大 值 即 可 。 每种状态转移时,分别在两种情况里取一个较大值即可。 每种状态转移时,分别在两种情况里取一个较大值即可。
注意: 求 最 大 值 问 题 , f 数 组 初 始 化 为 − ∞ 。 考 虑 边 界 问 题 , 根 据 状 态 转 移 方 程 , f [ i ] [ 0 ] [ 0 ] , i ∈ [ 0 , n ] , 会 被 考 虑 n 次 , 这 里 要 初 始 化 为 0 。 求最大值问题,f数组初始化为-∞。\\考虑边界问题,根据状态转移方程,f[i][0][0],i∈[0,n],会被考虑n次,这里要初始化为0。 求最大值问题,f数组初始化为−∞。考虑边界问题,根据状态转移方程,f[i][0][0],i∈[0,n],会被考虑n次,这里要初始化为0。
代码:
#include2、股票买卖 V
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
输入格式
第一行包含整数 N,表示数组长度。
第二行包含 N 个不超过 10000 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105
输入样例:
5
1 2 3 0 2
输出样例:
3
样例解释
对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出],第一笔交易可得利润 2-1 = 1,第二笔交易可得利润 2-0 = 2,共得利润 1+2 = 3。
分析:
有 天 数 限 制 的 股 票 买 卖 问 题 。 有天数限制的股票买卖问题。 有天数限制的股票买卖问题。
f [ i , k ] : 表 示 考 虑 前 i 天 的 股 票 , 第 i 天 的 状 态 是 k 的 最 大 收 益 。 k = 0 o r 1 o r 2 。 f[i,k]:表示考虑前i天的股票,第i天的状态是k的最大收益。k= \ 0\ or\ 1 \ or\ 2。 f[i,k]:表示考虑前i天的股票,第i天的状态是k的最大收益。k= 0 or 1 or 2。
0 : 表 示 手 中 有 货 ; 1 : 表 示 手 中 无 货 的 第 1 天 。 2 : 表 示 手 中 无 货 的 第 j 天 ( j > = 2 ) 。 0:表示手中有货;\ 1:表示手中无货的第1天。\ 2:表示手中无货的第j天(j>=2)。 0:表示手中有货; 1:表示手中无货的第1天。 2:表示手中无货的第j天(j>=2)。
共 3 种 状 态 , 5 种 转 移 的 可 能 。 共3种状态,5种转移的可能。 共3种状态,5种转移的可能。
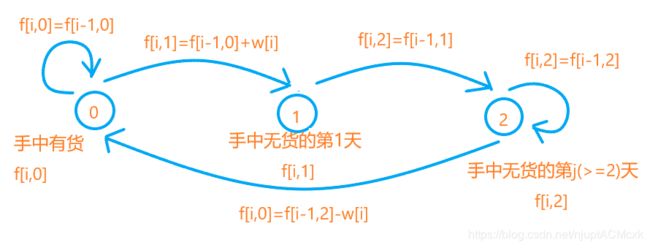
当 k = 0 时 , 第 i 天 手 中 有 股 票 , ① 、 本 来 第 i − 1 天 手 中 就 有 股 票 , 第 i 天 不 买 , f [ i , 0 ] = f [ i − 1 , 0 ] 。 ② 、 本 来 第 i − j 天 ( j > = 2 ) 手 中 没 股 票 , 在 第 i 天 买 入 股 票 , f [ i , 0 ] = f [ i − 1 , 2 ] − w [ i ] 。 当k=0时,第i天手中有股票,\\①、本来第i-1天手中就有股票,第i天不买,f[i,0]=f[i-1,0]。\\②、本来第i-j天(j>=2)手中没股票,在第i天买入股票,f[i,0]=f[i-1,2]-w[i]。 当k=0时,第i天手中有股票,①、本来第i−1天手中就有股票,第i天不买,f[i,0]=f[i−1,0]。②、本来第i−j天(j>=2)手中没股票,在第i天买入股票,f[i,0]=f[i−1,2]−w[i]。
当 k = 1 时 , 第 i 天 是 手 中 无 股 票 的 第 1 天 , 即 卖 掉 了 前 一 天 手 上 的 股 票 , f [ i , 1 ] = f [ i − 1 , 0 ] + w [ i ] 。 当k=1时,第i天是手中无股票的第1天,即卖掉了前一天手上的股票,f[i,1]=f[i-1,0]+w[i]。 当k=1时,第i天是手中无股票的第1天,即卖掉了前一天手上的股票,f[i,1]=f[i−1,0]+w[i]。
当 k = 2 时 , 第 i 天 是 手 中 无 股 票 的 第 j ( j > = 2 ) 天 , ① 、 j = 2 , 本 来 第 i − 1 天 是 没 有 股 票 的 第 1 天 , f [ i , 2 ] = f [ i − 1 , 1 ] 。 ② 、 j > = 3 , 本 来 第 i − 1 天 是 没 有 股 票 的 第 j − 1 天 , f [ i , 2 ] = f [ i − 1 , 2 ] 。 当k=2时,第i天是手中无股票的第j(j>=2)天,\\①、j=2,本来第i-1天是没有股票的第1天,f[i,2]=f[i-1,1]。\\②、j>=3,本来第i-1天是没有股票的第j-1天,f[i,2]=f[i-1,2]。 当k=2时,第i天是手中无股票的第j(j>=2)天,①、j=2,本来第i−1天是没有股票的第1天,f[i,2]=f[i−1,1]。②、j>=3,本来第i−1天是没有股票的第j−1天,f[i,2]=f[i−1,2]。
对 每 种 状 态 的 子 状 态 取 一 个 较 大 值 即 可 。 对每种状态的子状态取一个较大值即可。 对每种状态的子状态取一个较大值即可。
边 界 的 处 理 : 初 始 状 态 是 在 f [ 0 ] [ 2 ] , f [ 0 ] [ 0 ] = f [ 0 ] [ 1 ] 均 会 被 用 到 , 初 始 化 为 − ∞ 。 边界的处理:\\初始状态是在f[0][2],f[0][0]=f[0][1]均会被用到,初始化为-∞。 边界的处理:初始状态是在f[0][2],f[0][0]=f[0][1]均会被用到,初始化为−∞。
代码:
#include