凸优化学习(二)——凸集
注意,本文内容来自于吴恩达老师cs229课堂笔记的中文翻译项目:https://github.com/Kivy-CN/Stanford-CS-229-CN 中的凸优化部分的内容进行翻译学习。
2. 凸集
我们从凸集的概念开始研究凸优化问题。
定义2.1 我们定义一个集合是凸的,当且仅当任意 x , y ∈ C x,y\in C x,y∈C 且 θ ∈ R , 0 ≤ θ ≤ 1 \theta\in R, 0\le\theta\le 1 θ∈R,0≤θ≤1,
θ x + ( 1 − θ ) y ∈ C \theta x + (1-\theta)y\in C θx+(1−θ)y∈C
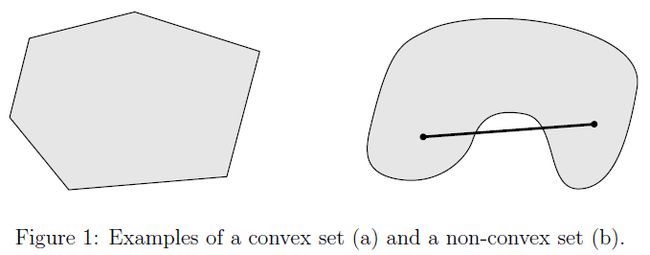
实际上,这意味着如果我们在集合 C C C中取任意两个元素,在这两个元素之间画一条直线,那么这条直线上的每一点都属于 C C C。图 1 1 1显示了一个示例的一个凸和一个非凸集。其中点 θ x + ( 1 − θ ) y \theta x +(1-\theta) y θx+(1−θ)y被称作点集 x , y x,y x,y的凸性组合(convex combination)。
2.1 凸集的实例
-
全集 R n R^n Rn 是一个凸集 (译者注:即 n n n维向量空间或线性空间中所有元素组成的集合)。 因为以下结论显而易见:任意 x , y ∈ R n x,y\in R^n x,y∈Rn,则 θ x + ( 1 − θ ) y ∈ R n \theta x +(1-\theta) y\in R^n θx+(1−θ)y∈Rn。(译者注: n n n维向量空间对加法和数乘封闭,显然其线性组合也封闭)
-
非负的象限 R + n R^n_+ R+n组成的集合 是一个凸集。 R n R^n Rn中所有非负的元素组成非负象限: R + n = { x : x i ≥ 0 ∀ i = 1 , … , n } R^n_+=\{x:x_i\ge 0\quad\forall i=1,\dots,n \} R+n={x:xi≥0∀i=1,…,n}。为了证明 R + n R^n_+ R+n是一个凸集,只要给定任意 x , y ∈ R + n x,y\in R^n_+ x,y∈R+n,并且 0 ≤ θ ≤ 1 0\le\theta\le 1 0≤θ≤1,
( θ x + ( 1 − θ ) y ) i = θ x i + ( 1 − θ ) y i ≥ 0 ∀ i (\theta x +(1-\theta) y)_i = \theta x_i + (1 - \theta)y_i\ge 0\quad\forall i (θx+(1−θ)y)i=θxi+(1−θ)yi≥0∀i
- 范数球是一个凸集。设 ∥ ⋅ ∥ \parallel\cdot\parallel ∥⋅∥是 R n R^n Rn中的一个范数(例如,欧几里得范数,即二范数 ∥ x ∥ 2 = ∑ i = 1 n x i 2 \parallel x\parallel_2=\sqrt{\sum_{i=1}^nx_i^2} ∥x∥2=∑i=1nxi2)。则集合 { x : ∥ x ∥ ≤ 1 } \{x:\parallel x\parallel\le 1\} {x:∥x∥≤1}是一个凸集。为了证明这个结论,假设 x , y ∈ R n x,y\in R^n x,y∈Rn,其中 ∥ x ∥ ≤ 1 , ∥ y ∥ ≤ 1 , 0 ≤ θ ≤ 1 \parallel x\parallel\le 1,\parallel y\parallel\le 1,0\le\theta\le 1 ∥x∥≤1,∥y∥≤1,0≤θ≤1,则:
∥ θ x + ( 1 − θ ) y ∥ ≤ ∥ θ x ∥ + ∥ ( 1 − θ ) y ∥ = θ ∥ x ∥ + ( 1 − θ ) ∥ y ∥ ≤ 1 \parallel \theta x +(1-\theta) y\parallel\le \parallel\theta x\parallel+\parallel(1-\theta) y\parallel = \theta\parallel x\parallel+(1-\theta)\parallel y\parallel\le 1 ∥θx+(1−θ)y∥≤∥θx∥+∥(1−θ)y∥=θ∥x∥+(1−θ)∥y∥≤1
我们用了三角不等式和范数的正同质性(positive homogeneity)。
- 仿射子空间和多面体 是一个凸集。给定一个矩阵 A ∈ R m × n A\in R^{m\times n} A∈Rm×n和一个向量 b ∈ R m b\in R^m b∈Rm,一个仿射子空间可以表示成一个集合 { x ∈ R n : A x = b } \{x\in R^n:Ax=b\} {x∈Rn:Ax=b}(注意如果 b b b无法通过 A A A列向量的线性组合得到时,结果可能是空集)。类似的,一个多面体(同样,也可能是空集)是这样一个集合 { x ∈ R n : A x ⪯ b } \{x\in R^n:Ax\preceq b\} {x∈Rn:Ax⪯b},其中‘ ⪯ \preceq ⪯’代表分量不等式(componentwise inequality)(也就是, A x Ax Ax得到的向量中的所有元素都小于等于 b b b向量对应位置的元素) 1 ^1 1。为了证明仿射子空间和多面体是凸集,首先考虑 x , y ∈ R n x,y\in R^n x,y∈Rn,这样可得 A x = A y = b Ax=Ay=b Ax=Ay=b。则对于 0 ≤ θ ≤ 1 0\le\theta\le 1 0≤θ≤1,有:
1 类似的,对于两个向量 x , y ∈ R n x,y\in R^n x,y∈Rn, x ⪰ y x\succeq y x⪰y代表,向量 x x x中的每一个元素都大于等于向量 y y y对应位置的元素。注意有时候文中使用符号‘ ≤ \le ≤’和‘ ≥ \ge ≥’代替了符号‘ ⪯ \preceq ⪯’和‘ ⪰ \succeq ⪰’,则符号的实际意义必须根据上下文来确定(也就是如果等式两边都是向量的时候,文中使用的是常规的不等号‘ ≤ \le ≤’和‘ ≥ \ge ≥’,则我们自己心中要知道用后两个符号‘ ⪯ \preceq ⪯’和‘ ⪰ \succeq ⪰’的意义代替之)
A ( θ x + ( 1 − θ ) y ) = θ A x + ( 1 − θ ) A y = θ b + ( 1 − θ ) b = b A(\theta x +(1-\theta) y) = \theta Ax + (1-\theta)Ay=\theta b + (1-\theta)b=b A(θx+(1−θ)y)=θAx+(1−θ)Ay=θb+(1−θ)b=b
类似的,对于 x , y ∈ R n x,y\in R^n x,y∈Rn,满足 A x ≤ b Ax\le b Ax≤b以及 A y ≤ b , 0 ≤ θ ≤ 1 Ay\le b,0\le\theta\le 1 Ay≤b,0≤θ≤1,则:
A ( θ x + ( 1 − θ ) y ) = θ A x + ( 1 − θ ) A y ≤ θ b + ( 1 − θ ) b = b A(\theta x +(1-\theta) y) = \theta Ax + (1-\theta)Ay\le\theta b + (1-\theta)b=b A(θx+(1−θ)y)=θAx+(1−θ)Ay≤θb+(1−θ)b=b
- 凸集之间的交集还是凸集。假设 C 1 , C 2 , … , C k C_1,C_2,\dots,C_k C1,C2,…,Ck都是凸集,则它们的交集:
⋂ i = 1 k C i = { x : x ∈ C i ∀ i = 1 , … , k } \bigcap_{i=1}^kC_i=\{x:x\in C_i\quad\forall i=1,\dots,k\} i=1⋂kCi={x:x∈Ci∀i=1,…,k}
同样也是凸集。为了证明这个结论,考虑 x , y ∈ ⋂ i = 1 k C i x,y\in \bigcap_{i=1}^k C_i x,y∈⋂i=1kCi以及 0 ≤ θ ≤ 1 0\le\theta\le 1 0≤θ≤1,则:
θ x + ( 1 − θ ) y ∈ C i ∀ i = 1 , ⋯ , k \theta x +(1-\theta) y\in C_i\quad\forall i=1,\cdots,k θx+(1−θ)y∈Ci∀i=1,⋯,k
因此,根据凸集的定义可得:
θ x + ( 1 − θ ) y ∈ ⋂ i = 1 k C i \theta x +(1-\theta) y\in\bigcap_{i=1}^kC_i θx+(1−θ)y∈i=1⋂kCi
然而要注意在通常情况下,凸集之间的并集并不是一个凸集。
- 半正定矩阵是一个凸集。所有对称正半定矩阵的集合,常称为正半定锥,记作 S + n S^n_+ S+n,其是一个凸集(通常情况下, S n ⊂ R n × n S^n\subset R^{n\times n} Sn⊂Rn×n代表 n × n n\times n n×n对称矩阵的集合)。回忆一个概念,我们说一个矩阵 A ∈ R n × n A\in R^{n\times n} A∈Rn×n是对称半正定矩阵,当且仅当该矩阵满足 A = A T A=A^T A=AT,并且给定任意一个 n n n维向量 x ∈ R n x\in R^n x∈Rn,满足 x T A x ≥ 0 x^TAx\ge 0 xTAx≥0。现在考虑两个对称半正定矩阵 A , B ∈ S + n A,B\in S^n_+ A,B∈S+n,并且有 0 ≤ θ ≤ 1 0\le\theta\le 1 0≤θ≤1。给定任意 n n n维向量 x ∈ R n x\in R^n x∈Rn,则:
x T ( θ A + ( 1 − θ ) B ) x = θ x T A x + ( 1 − θ ) x T B x ≥ 0 x^T(\theta A +(1-\theta) B)x=\theta x^TAx+(1-\theta)x^TBx\ge 0 xT(θA+(1−θ)B)x=θxTAx+(1−θ)xTBx≥0
同样的逻辑可以用来证明所有正定、负定和负半定矩阵的集合也是凸集。
下一篇:凸优化学习(三)——凸函数