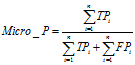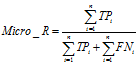转自:
http://blog.csdn.net/sinat_26917383/article/details/75199996?locationNum=3&fps=1
http://www.cnblogs.com/robert-dlut/p/5276927.html
http://d0evi1.com/sklearn/model_evaluation/
谈谈评价指标中的宏平均和微平均
谈谈评价指标中的宏平均和微平均
今天在阅读周志华老师的《机器学习》一书时,看到性能度量这一小节,里面讲到了宏平均和微平均的计算方法,这也是我一直没有很清晰的一个概念,于是在看了之后又查阅了一些资料,但是还是存在一些问题,想和大家分享一下。
(1)召回率、准确率、F值
对于二分类问题,可将样例根据其真实类别和分类器预测类别划分为:
-
真正例(True Positive,TP):真实类别为正例,预测类别为正例。
-
假正例(False Positive,FP):真实类别为负例,预测类别为正例。
-
假负例(False Negative,FN):真实类别为正例,预测类别为负例。
-
真负例(True Negative,TN):真实类别为负例,预测类别为负例。
然后可以构建混淆矩阵(Confusion Matrix)如下表所示。
真实类别 |
预测类别 |
正例 |
负例 |
正例 |
TP |
FN |
负例 |
FP |
TN |
准确率,又称查准率(Precision,P):
(1) 
召回率,又称查全率(Recall,R):
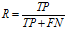 (2)
(2)
F1值:
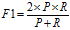 (3)
(3)
F1的一般形式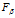 :
:
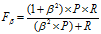 (4)
(4)
如果只有一个二分类混淆矩阵,那么用以上的指标就可以进行评价,没有什么争议,但是当我们在n个二分类混淆矩阵上要综合考察评价指标的时候就会用到宏平均和微平均。
(2)宏平均(Macro-averaging)和微平均(Micro-averaging)
宏平均(Macro-averaging),是先对每一个类统计指标值,然后在对所有类求算术平均值。
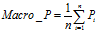 (5)
(5)
 (6)
(6)
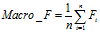 (7)
(7)
 (8)
(8)
微平均(Micro-averaging),是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵,然后计算相应指标。
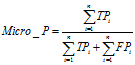 (9)
(9)
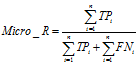 (10)
(10)

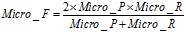 (11)
(11)
从上面的公式我们可以看到微平均并没有什么疑问,但是在计算宏平均F值时我给出了两个公式分别为公式(7)和(8)。这两个公式就是我疑惑的地方,因为我在不同的论文中看到了不同的宏平均F值的计算方法,例如在参考资料的[3][4]。于是我试图查阅宏平均和微平均提出的初始论文。但是可能由于时间比较久远还是某些原因,我并没有找到最早提出的论文,而大多数论文使用它们的时候引用比较多的是(Yang 1999)的这篇论文,论文中也未明确给出宏平均F值的计算公式,但是根据其描述:
"For evaluating performance average across categories, there are two conventional methods, namely macro-averaging and micro-averaging. Macro-averaged performance scores are computed by first computing the scores for the per-category contingency tables and then averaging these per-category scores to compute the global means. Micro-averaged performance scores are computed by first creating a global contingency table whose cell values are the sums of the corresponding cells in the per-category contingency tables, and then use this global contingency table to compute the micro-averaged performance scores"
可以看到论文里的宏平均F值应该按照公式(7)计算。但是在不少论文中我也看到了公式(8)的计算方法,所以在这可能并没有一个定论,我也比较困惑。
在参加评测中,评价指标计算都是由主办方制定并进行计算,一般会有明确的计算公式,我在这里想说的是在不少论文中使用宏平均F值时并未给出明确的计算公式,可能会存在两种不同的算法,在论文进行结果比较时,可能会有所差异。
参考资料:
1. 周志华. 机器学习.清华大学出版社
2. Yang Y. An evaluation of statistical approaches to text categorization[J]. Information retrieval, 1999, 1(1-2): 69-90.
3. 杨杰明. 文本分类中文本表示模型和特征选择算法研究. 吉林大学博士论文.
4. 廖一星. 文本分类及其特征降维研究. 浙江大学博士论文.
一、acc、recall、F1、混淆矩阵、分类综合报告
1、准确率
第一种方式:accuracy_score
import numpy as np
from sklearn.metrics import accuracy_score
y_pred = [0, 2, 1, 3,9,9,8,5,8]
y_true = [0, 1, 2, 3,2,6,3,5,9]
accuracy_score(y_true, y_pred)
Out[127]: 0.33333333333333331
accuracy_score(y_true, y_pred, normalize=False)
Out[128]: 3
第二种方式:metrics
宏平均比微平均更合理,但也不是说微平均一无是处,具体使用哪种评测机制,还是要取决于数据集中样本分布
宏平均(Macro-averaging),是先对每一个类统计指标值,然后在对所有类求算术平均值。
微平均(Micro-averaging),是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵,然后计算相应指标。(来源:谈谈评价指标中的宏平均和微平均)
from sklearn import metrics
metrics.precision_score(y_true, y_pred, average='micro')
Out[130]: 0.33333333333333331
metrics.precision_score(y_true, y_pred, average='macro')
Out[131]: 0.375
metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro')
Out[133]: 0.5
其中average参数有五种:(None, ‘micro’, ‘macro’, ‘weighted’, ‘samples’)
.
2、召回率
metrics.recall_score(y_true, y_pred, average='micro')
Out[134]: 0.33333333333333331
metrics.recall_score(y_true, y_pred, average='macro')
Out[135]: 0.3125
.
3、F1
metrics.f1_score(y_true, y_pred, average='weighted')
Out[136]: 0.37037037037037035
.
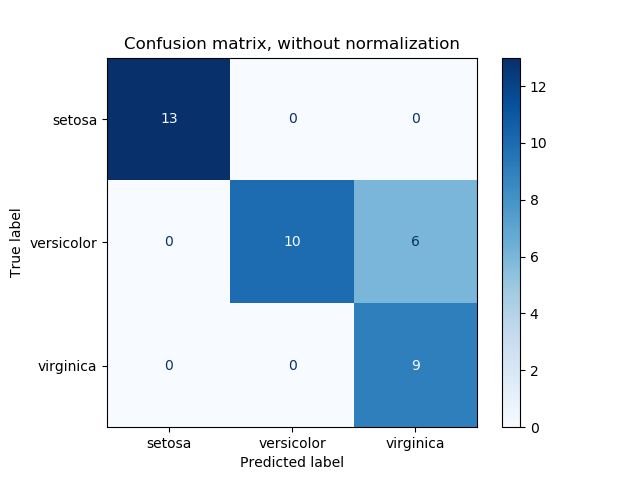
4、混淆矩阵
from sklearn.metrics import confusion_matrix
confusion_matrix(y_true, y_pred)
Out[137]:
array([[1, 0, 0, ..., 0, 0, 0],
[0, 0, 1, ..., 0, 0, 0],
[0, 1, 0, ..., 0, 0, 1],
...,
[0, 0, 0, ..., 0, 0, 1],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 1, 0]])
横为true label 竖为predict
.
5、 分类报告
from sklearn.metrics import classification_report
y_true = [0, 1, 2, 2, 0]
y_pred = [0, 0, 2, 2, 0]
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_true, y_pred, target_names=target_names))
其中的结果:
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 1.00 1.00 2
avg / total 0.67 0.80 0.72 5
- 包含:precision/recall/fi-score/均值/分类个数
.
6、 kappa score
kappa score是一个介于(-1, 1)之间的数. score>0.8意味着好的分类;0或更低意味着不好(实际是随机标签)
from sklearn.metrics import cohen_kappa_score
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
cohen_kappa_score(y_true, y_pred)
.
二、ROC
1、计算ROC值
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
roc_auc_score(y_true, y_scores)
2、ROC曲线
y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)
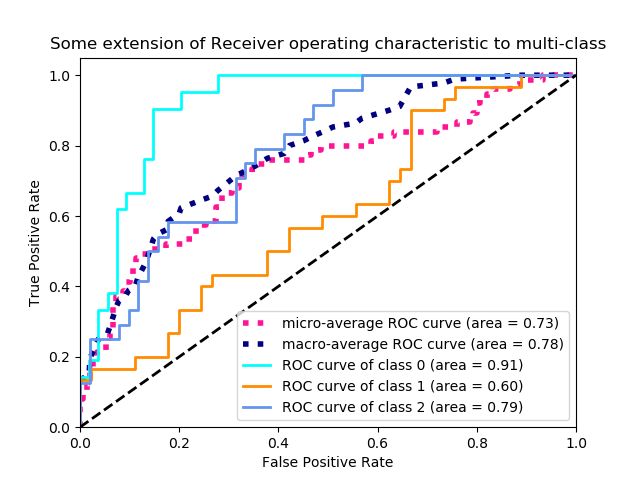
来看一个官网例子,贴部分代码,全部的code见:Receiver Operating Characteristic (ROC)
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
from scipy import interp
iris = datasets.load_iris()
X = iris.data
y = iris.target
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
mean_tpr += interp(all_fpr, fpr[i], tpr[i])
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
plt.figure()
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(n_classes), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()
.
三、距离
.
1、海明距离
from sklearn.metrics import hamming_loss
y_pred = [1, 2, 3, 4]
y_true = [2, 2, 3, 4]
hamming_loss(y_true, y_pred)
0.25
.
2、Jaccard距离
import numpy as np
from sklearn.metrics import jaccard_similarity_score
y_pred = [0, 2, 1, 3,4]
y_true = [0, 1, 2, 3,4]
jaccard_similarity_score(y_true, y_pred)
0.5
jaccard_similarity_score(y_true, y_pred, normalize=False)
2
.
四、回归
1、 可释方差值(Explained variance score)
from sklearn.metrics import explained_variance_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
explained_variance_score(y_true, y_pred)
.
2、 平均绝对误差(Mean absolute error)
from sklearn.metrics import mean_absolute_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mean_absolute_error(y_true, y_pred)
.
3、 均方误差(Mean squared error)
from sklearn.metrics import mean_squared_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mean_squared_error(y_true, y_pred)
.
4、中值绝对误差(Median absolute error)
from sklearn.metrics import median_absolute_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
median_absolute_error(y_true, y_pred)
.
5、 R方值,确定系数
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
r2_score(y_true, y_pred)
![]()
![]() (2)
(2) ![]() (3)
(3) ![]() :
:![]() (4)
(4) ![]() (5)
(5)![]() (6)
(6)![]() (7)
(7)![]() (8)
(8) ![]()
![]() (11)
(11)