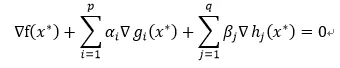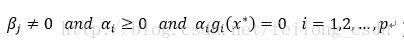KKT条件--约束问题最优化方法

KKT条件:

KKT可以概括为以下三个条件：
1）最优点x必须满足所有等式及不等式限制条件, 也就是说最优点必须是一个可行解

2）在最优点x, ∇f 必须是 ∇gi 和 ∇hj 的线性組合（α和β是拉格朗日乘子）

3）该条件是对拉格朗日乘子不等式的一些限制（α和β是拉格朗日乘子）
对于不等式的拉格朗日乘子限制条件有方向性, 所以每一个α都必须大于或等于零, 而等式限制条件没有方向性，只是β不等于0。

 

详述：https://www.cnblogs.com/ooon/p/5721119.html

 提到KKT条件一般会附带的提一下拉格朗日乘子。对学过高等数学的人来说比较拉格朗日乘子应该会有些印象。二者均是求解最优化问题的方法，不同之处在于应用的情形不同。一般情况下，最优化问题会碰到一下三种情况：

（1）无约束条件

（2）等式约束条件

（3）不等式约束条件

 

 

 

 

凸优化问题 

拉格朗日函数

对偶问题

什么是对偶问题？这可以牵扯到认知世界的方法论。比如我们永远无法知道别人眼中的自己是什么样的，有趣的是我们往往不关心自己是否真的好看，而更希望别人认为我们好看，这其实是两个问题（所以美颜相机会如此风靡全球）。如果后者是优化的原问题，那前者就是这个问题的对偶问题。因为我们没办法知道别人眼中的自己是什么样子，所以我们只能通过优化对偶问题（对着镜子打扮）来间接地优化原问题。

 

https://blog.csdn.net/zjsmdchen/article/details/51079821 

https://www.jianshu.com/p/c3e23bf233f8