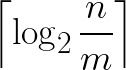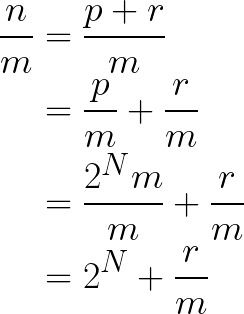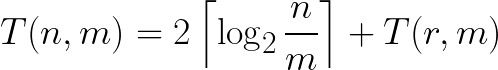序言
7月初的时候挑战了一下LeetCode的第29题(中等难度,似乎没什么值得夸耀的),题目要求在不使用除、乘,以及模运算的情况下,实现整数相除的函数。
既然被除数和除数都是整数,那么用减法就可以实现除除法了(多么naive的想法)。一个trivial的、用JavaScript编写的函数可以是下面这样的(为了简单起见,只考虑两个参数皆为正整数的情况)
function divide(n, m) {
let acc = 0;
while (n >= m) {
n -= m;
acc += 1;
}
return acc;
}如此朴素的divide函数提交给LeetCode是不会被接受的的——它会在像2147483648除以2这样的测试用例上超时。可以在本地运行一下感受下究竟有多慢
➜ nodejs time node divide.js
2147483648/2=1073741824
node divide.js 1.14s user 0.01s system 99% cpu 1.161 total那么有没有更快的计算两个整数的商的算法呢?答案当然是肯定的。
尝试优化
一眼就可以看出,运行次数最多的是其中的while循环。以2147483648除以2为例,while循环中的语句要被执行1073741824次。为了提升运行速度,必须减少循环的次数。
既然每次从n中减去m需要执行n/m次,那么如果改为每次从中减去2m,不就只需要执行(n/m)/2次了么?循环的次数一下子就减少了一半,想想都觉得兴奋啊。每次减2m,并且自增2的算法的代码及其运行效果如下
➜ nodejs cat divide2.js
function divide(n, m) {
let acc = 0;
let m2 = m << 1; // 因为题目要求不能用乘法,所以用左移来代替乘以2。
while (n >= m2) {
n -= m2;
acc += 2;
}
while (n >= m) {
n -= m;
acc += 1;
}
return acc;
}
console.log(`2147483648/2=${divide(2147483648, 2)}`);
➜ nodejs time node divide2.js
2147483648/2=1073741824
node divide2.js 2.65s user 0.01s system 99% cpu 2.674 total尽管耗时不降反升,令场面一度十分尴尬,但根据理论分析可知,第一个循环的运行次数仅为原来的一半,而第二个循环的运行次数最多为1次,可以知道这个优化的方向是没问题的。
如果计算m2的时候左移的次数为2,那么acc的自增步长需要相应地调整为4,第一个循环的次数将大幅下降至268435456,第二个循环的次数不会超过4;如果左移次数为3,那么acc的步长增至8,第一个循环的次数降至134217728,第二个循环的次数不会超过8。
显然,左移不能无限地进行下去,因为m2的值早晚会超过n。很容易算出左移次数的一个上限为
对数符号意味着即便对于很大的n和很小的m,上述公式的结果也不会很大,因此可以显著地提升整数除法的计算效率。
在开始写代码前,让我先来简单地证明一下这个方法算出来的商与直接计算n/m是相等的。
一个简单的证明
记被减数为n,减数为m。显然,存在一个正整数N,使得
令
,再令
![]()
,那么n除以m等价于
证明完毕。
从上面的公式还可以知道,新算法将原本规模为n的问题转换为了一个规模为r的相同问题,这意味着可以用递归的方式来优雅地编写最终的代码。
完整的代码
最终的divide函数的代码如下
function divide(n, m) {
if (n < m) {
return 0;
}
let n2 = n;
let N = 0;
// 用右移代替左移,避免溢出。
while ((n2 >> 1) > m) {
N += 1;
n2 = n2 >> 1;
}
// `power`表示公式中2的N次幂
// `product`代表`power`与被除数`m`的乘积
let power = 1;
let product = m;
for (let i = 0; i < N; i++) {
power = power << 1;
product = product << 1;
}
return power + divide(n - product, m);
}这个可比最开始的divide要快得多了,有图有真相
➜ nodejs time node divide3.js
2147483648/2=1073741824
node divide3.js 0.03s user 0.01s system 95% cpu 0.044 total后记
如果以T(n, m)表示被除数为n,除数为m时的算法时间复杂度,那么它的递推公式可以写成下列的形式
但这玩意儿看起来并不能用主定理直接求出解析式,所以很遗憾,我也不知道这个算法的时间复杂度究竟如何——尽管我猜测就是N的计算公式。
如果有哪位好心的读者朋友知道的话,还望不吝赐教。