机器学习系列(4)——梯度下降
梯度下降法
在回归问题的第三步中,需要解决下面的最优化问题:
θ ∗ = a r g min θ L ( θ ) \theta^*=arg\min_\theta L(\theta) θ∗=argminθL(θ)
- L:loss function(损失函数)
- θ \theta θ:parameters(参数)
这是的parameters是复数,即 θ \theta θ指代一堆参数,比如之前说到的w和b。我们要找一组参数 θ \theta θ,让损失函数越小越好,这个问题可以用梯度下降法解决:
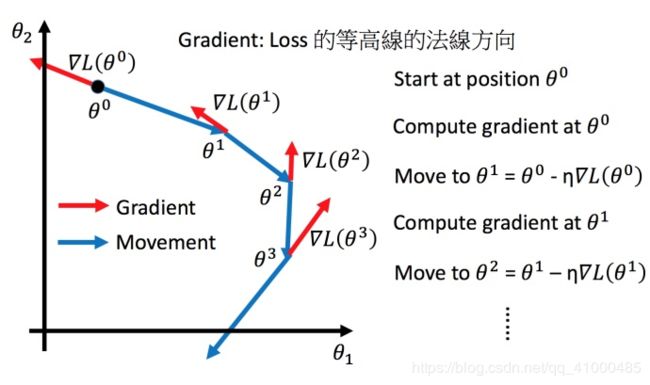
假设 θ \theta θ里面有两个参数 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2

先随机选取初始值,然后分别计算初始点处,两个参数对L的偏微分,然后 θ 0 \theta^0 θ0减掉 η \eta η乘上偏微分的值,得到一组新的参数。同理反复进行这样的计算。黄色部分即为间接写法。 ∇ L ( θ ) \nabla L(\theta) ∇L(θ)即为梯度。 η \eta η叫做Learning rate(学习率)。可视化过程如下:
优化Tips
Tip1:调整学习率
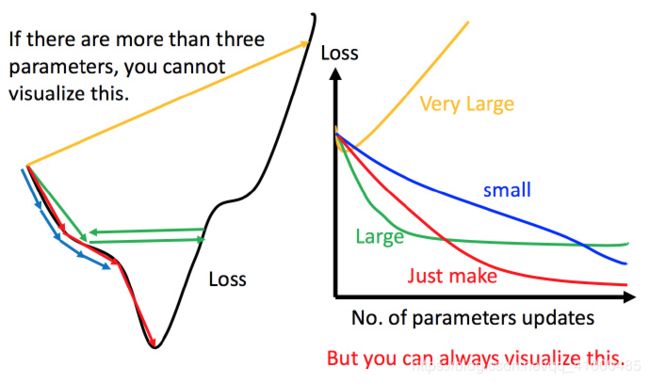
上图左边褐色为损失函数的曲线,假设从左边最高点开始,如果学习率调整的刚刚好,比如红色的线,就能顺利找到最低点。如果学习率调整的太小,比如蓝色的线,就会走的太慢,虽然这种情况给足够的时间也可以找到最低点,实际情况可能会等不及出结果。如果学习率调整的有点大,比如绿色的曲线,就会在上面震荡,走不下去,永远无法到达最低点。还有可能非常大,比如黄色的线,直接就飞出去了,更新参数的时候指挥发现损失函数越更新越大。
虽然这样的可视化可以很直观的观察,但可视化也只能是在参数是一维或者二维的时候进行,更高维的情况已经无法可视化了。
解决方法就是上图右边的方法,将参数改变对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的特别慢;学习率太大(绿色的线),损失函数下降的很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。
举一个简单的思想:随着次数的增加,通过一些因子来减少学习率
- 通常刚开始,初始点会距离最低点比较远,所以用大一点的学习率
- update好几次参数之后呢,比较靠近最低点了,此时减少学习率
- 比如 η t = η t t + 1 \eta^t={\eta^t\over\sqrt {t+1}} ηt=t+1ηt,t是次数。随着次数的增加, η t \eta^t ηt减小
学习率不能是一个值通用所有的特征,不同的参数需要不同的学习率。
Adagrad算法
每个参数的学习率都把他除上之前微分的均方根。解释如下:
普通的梯度下降为:(w是一个参数)
w t + 1 ← w t − η t g t w^{t+1}\leftarrow w^t-\eta^tg^t wt+1←wt−ηtgt
η t = η t t + 1 \eta^t={\eta^t\over\sqrt {t+1}} ηt=t+1ηt
Adagrad可以做的更好:
( σ t \sigma^t σt:之前参数的所有微分的均方根,对于每个参数都是不一样的)
w t + 1 ← w t − η t σ t g t w^{t+1}\leftarrow w^t-{\eta^t\over \sigma^t}g^t wt+1←wt−σtηtgt
g t = ∂ L ( θ t ) ∂ w g^t={\partial L(\theta^t)\over \partial w} gt=∂w∂L(θt)
下图是一个参数的更新过程:
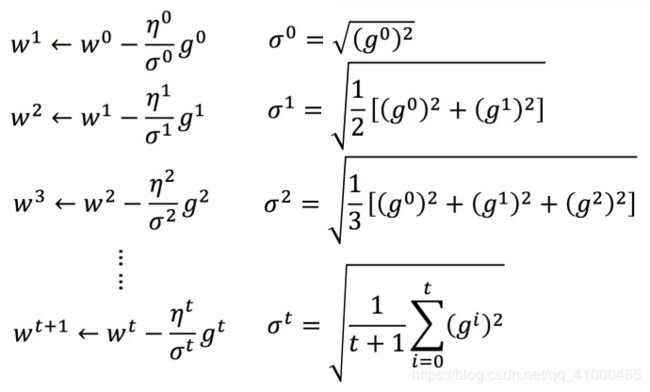
将Adagrad的式子进行化简:
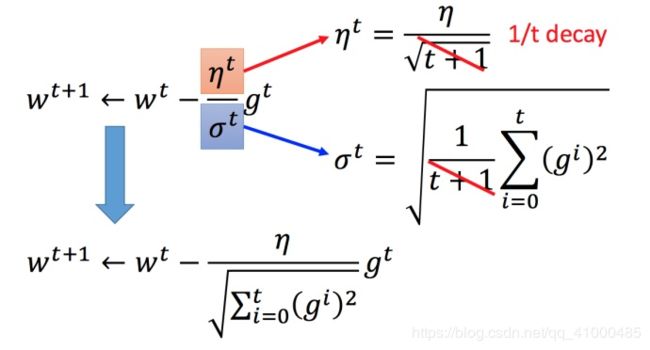
Adagrad存在的矛盾:
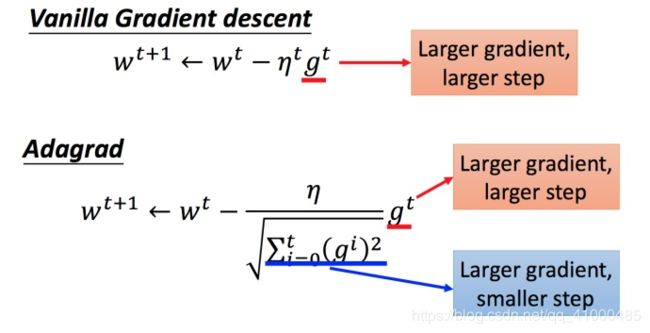
即在Adagrad中,当梯度越大的时候,步伐应该越大,但下面分母又导致当梯度越大的时候,步伐会越小。
正式解释:多参数下,梯度越大,跟最低点的距离不一定越远。
对比不同的参数
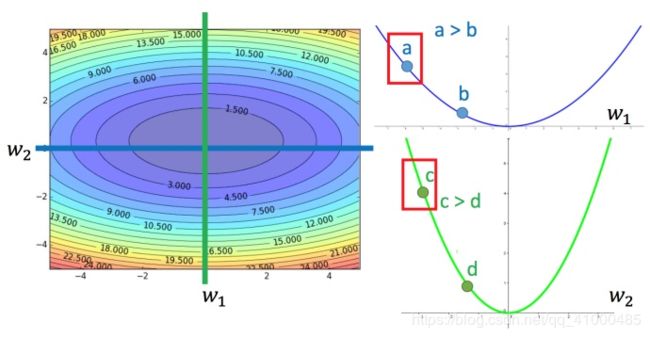
上图左边是两个参数的损失函数,颜色代表损失函数的值。如果只考虑参数 w 1 w_1 w1,就像图中蓝色的线,得到右边上图的结果;如果只考虑参数 w 2 w_2 w2,就像图中绿色的线,得到右边下图的结果。确实对于a和b,梯度越大,跟最低点的距离越远,同理c和d也成立。但是如果对比a和c,就不成立了,c比a大,但c距离最低点是比较近的。
所以最好的步伐应该是: 一 次 微 分 二 次 微 分 一次微分\over二次微分 二次微分一次微分
即不止和一次微分成正比,还和二次微分成反比。最好的step应该是考虑到二次微分。再回到之前的Adagrad,对于 ∑ i = 0 t ( g i ) 2 \sqrt{\sum_{i=0}^t(g^i)^2} ∑i=0t(gi)2就是希望在尽可能不增加过多运算的情况下模拟二次微分。(如果计算二次微分,在实际情况可能会增加很多的时间消耗)
Tip2:随机梯度下降法
之前的梯度下降:
L = ∑ n ( y ^ n − ( b + ∑ w i x i n ) ) 2 L=\sum_n(\hat y^n-(b+\sum w_ix_i^n))^2 L=∑n(y^n−(b+∑wixin))2
θ i = θ i − 1 − η ∇ L ( θ i − 1 ) \theta^i=\theta^{i-1}-\eta\nabla L(\theta^{i-1}) θi=θi−1−η∇L(θi−1)
而随机梯度下降法更快,损失函数不需要处理训练集的所有数据,选取一个例子 x n x^n xn:
L = ( y ^ n − ( b + ∑ w i x i n ) ) 2 L=(\hat y^n-(b+\sum w_ix_i^n))^2 L=(y^n−(b+∑wixin))2
θ i = θ i − 1 − η ∇ L ( θ i − 1 ) \theta^i=\theta^{i-1}-\eta\nabla L(\theta^{i-1}) θi=θi−1−η∇L(θi−1)
此时不需要像之前那样对对所有的数据进行处理,只需要计算某一个例子的损失函数Ln,就可以赶紧update梯度。下图对比:
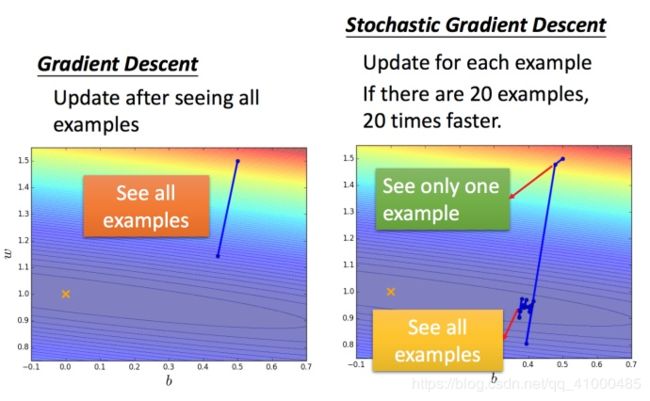
常规梯度下降法走一步要处理所有二十个例子,但随即算法此时已经走了二十步(每处理一个例子就更新)
Tip3:特征缩放
比如有个函数:
y = b + w 1 x 1 + w 2 x 2 y=b+w_1x_1+w_2x_2 y=b+w1x1+w2x2
两个输入的分布范围很不一样,建议把他们的范围缩放,使得不同输入的范围是不一样的。
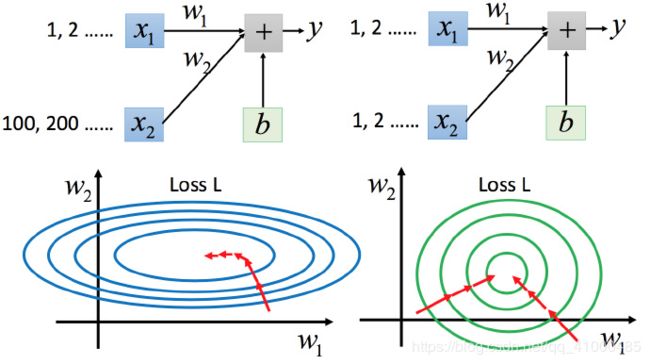
上图左边是 x 1 x_1 x1的scale要比 x 2 x_2 x2要小很多,所以当 w 1 w_1 w1和 w 2 w_2 w2做同样的变化时, w 1 w_1 w1对y的变化影响是比较小的, w 2 w_2 w2对 y y y的变化影响是比较大的。坐标系中是两个参数的error surface,先考虑左边蓝色,因 w 1 w_1 w1对 y y y的变化影响比较小,所以 w 1 w_1 w1对损失函数的影响比较小, w 1 w_1 w1对损失函数有比较小的微分,所以 w 1 w_1 w1方向上是比较平滑的。同理 w 2 w_2 w2对 y y y的影响比较大,所以 w 2 w_2 w2对损失函数的影响比较大,即在 w 2 w_2 w2方向有比较尖的峡谷。上图右边是两个参数scaling比较接近,右边的绿色图就比较接近圆形。
对于左边的情况,上面讲过这种狭长的情形不用Adagrad的话是比较难处理的,两个方向上需要不同的学习率,同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。左边的梯度下降并不是向最低点的方向走的,而是顺着等高线切线法线的方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也比较有效率。
缩放方法

上面每一列都是一个例子,里面都有一组特征。对每个维度i(绿色框)都计算平均数,记作 m i m_i mi;还要计算标准差,记作 σ i \sigma_i σi。然后用第r个例子中的第i个特征,减掉平均数 m i m_i mi,然后除以标准差 σ i \sigma_i σi,得到的结果是所有的平均数都是0,所有的方差都是1。
梯度下降的理论基础
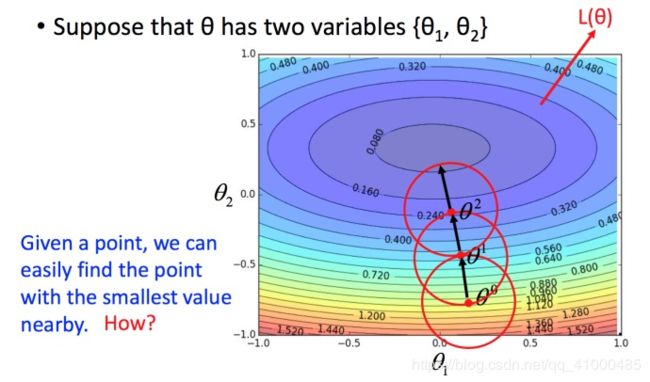
比如在 θ 0 \theta^0 θ0处,可以在一个小范围的圆圈内找到损失函数细小的 θ 1 \theta^1 θ1,不断的这样去寻找,接下来就是如何在小圆圈内快速的找到最小值?
泰勒展开式
定义:若 h ( x ) h(x) h(x)在 x = x 0 x=x_0 x=x0点的某个领域内有无限阶导数(即可无限微分,infinitely differentiable),那么在此领域内有:
h ( x ) = ∑ k = 0 ∞ h k ( x 0 ) k ! ( x − x 0 ) k = h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) + h ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + ⋅ ⋅ ⋅ h(x)=\sum_{k=0}^\infin {h^k(x_0)\over k!}(x-x_0)^k=h(x_0)+h'(x_0)(x-x_0)+{h''(x_0)\over2!}(x-x_0)^2+··· h(x)=∑k=0∞k!hk(x0)(x−x0)k=h(x0)+h′(x0)(x−x0)+2!h′′(x0)(x−x0)2+⋅⋅⋅
当 x x x很接近 x 0 x_0 x0时,有 h ( x ) ≈ h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) h(x)\approx h(x_0)+h'(x_0)(x-x_0) h(x)≈h(x0)+h′(x0)(x−x0)就是函数 h ( x ) h(x) h(x)在 x = x 0 x=x_0 x=x0点附近关于 x x x的幂函数展开式,也叫泰勒展开式。如下图所例:
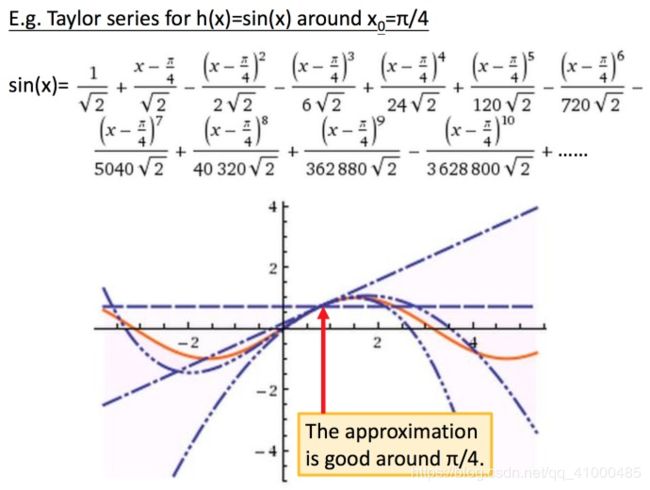
图中3条蓝色线就是把前三项作图,橙色线是 s i n ( x ) sin(x) sin(x)。
多变量泰勒展开式类似。如下图为两个变量的泰勒展开式:
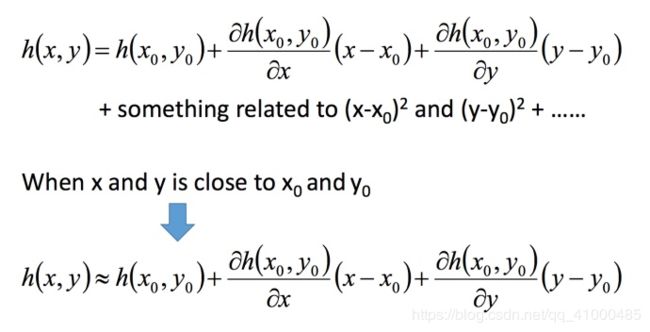
回到之前如何快速在圆圈内找到最小值,基于泰勒展开式,在 ( a , b ) (a,b) (a,b)点的红色圆圈范围内,可以将损失函数用泰勒展开式进行简化:
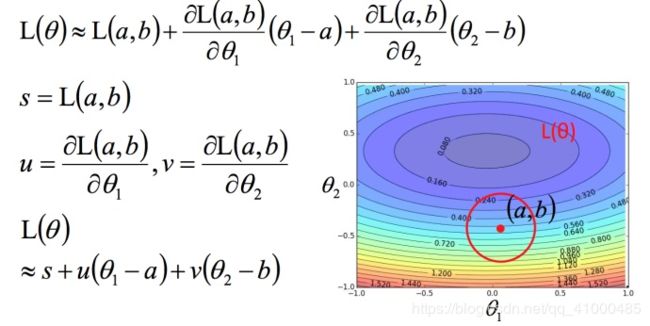
问题集如下的范围内的优化问题:
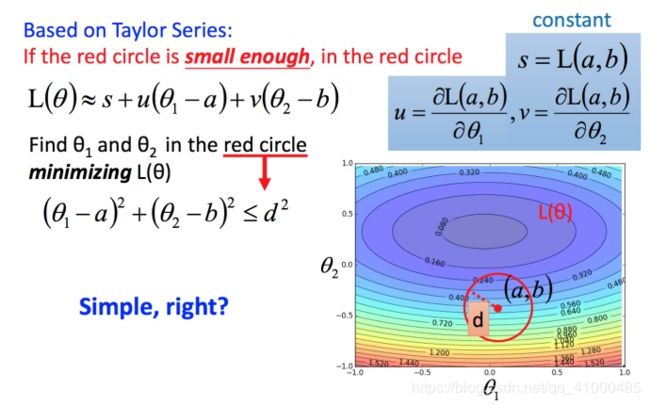
不考虑s的话,可以看出剩下的部分就是两个向量 ( Δ θ 1 , Δ θ 2 ) (\Delta\theta_1,\Delta\theta_2) (Δθ1,Δθ2)和 ( u , v ) (u,v) (u,v)的内积,那怎样让它最小,就是和向量 ( u , v ) (u,v) (u,v)方向相反的向量。
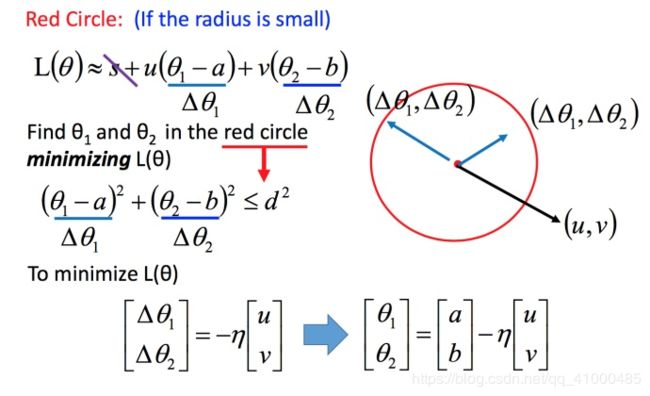

发现最后的式子就是梯度下降的式子。但这种方法找到这个式子有个前提,泰勒展开式给的损失函数的估算值是要足够精确的,而这需要红色的圆圈足够小(也就是学习率足够小)来保证。所以理论上每次更新参数都想要损失函数减小的话,就需要学习率足够小才可以。
所以十几种,当更新参数的时候,如果学习率没有设置好,有可能会导致做梯度下降的时候,损失函数没有越来越小。以上只考虑了泰勒展开式的一次项,如果考虑到二次项(比如牛顿法),在实际中不是特别好,会涉及到二次微分等,多很多的运算,性价比不好。
梯度下降的限制
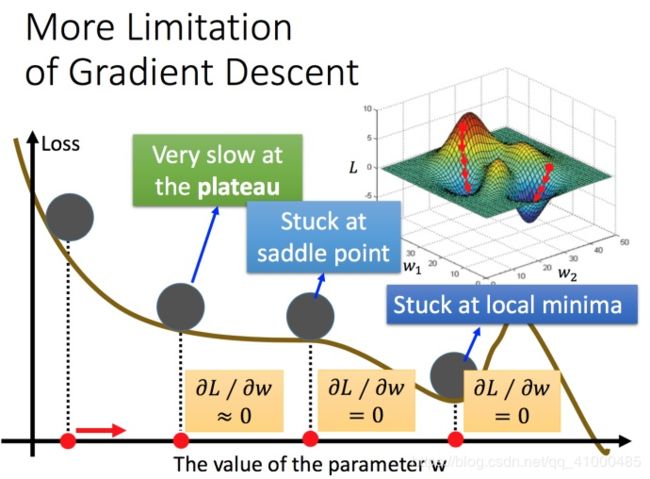
容易陷入局部极值,还有可能卡在不是极值,但微分值是0的地方,还有可能十几种当微分值小于某一个数值就停下来了,但这只是比较平缓,并不是极值点。