MATLAB聚类分析--------2019/8/22

聚类分析

• 定义：
  是对多个样本进行定量分析的多元统计分析方法。
  $$聚类分析=\{\begin{array}{l}Q型聚类分析：对样本进行分类\\ R型聚类分析：对指标进行分类\end{array}$$
• Q型聚类分析
  2.1. 样本的相似性度量
   用距离来度量样本点间的相似程度。
  
  
  2.2.类与类间的相似性度量
    如果有两个样本类G1和G2 ，我们可以用下面的一系列方法度量它们间的距离.
  
  
  
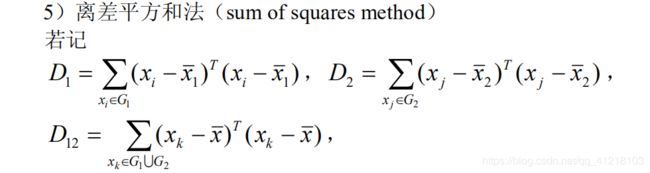
  2.3.系统聚类法
     Ⅰ、生成聚类图的步骤:
  （在平面上有 7 个点 $w_1,w_2,\cdots ,w_7$，设 $\Omega =\{w_1,w_2,\cdots ,w_7\}$）
    （1）计算 $n$ 个样本点两两之间的距离$\{d_{ij}\}$,记为矩阵 $D=(d_{ij}{)}_{n\times n}$
    （2）首先构造 $n$ 个类，每一个类中只包含一个样本点，每一类的平台高均为零；
    （3）合并距离最近的两类为新类，并且以这两类间的距离值作为聚类图中平台高度；
    （4）计算新类与当前各类的距离，若类的个数已经等于 1，转入步骤 5）否则，回到步骤（3）；
    （5）画聚类图；
    （6）决定类的个数和类。
  显而易见，这种系统归类过程与计算类和类之间的距离有关，采用不同的距离定义，有可能得出不同的聚类结果.
     Ⅱ、 最短距离法与最长距离法
  如果使用最短距离法来测量类与类之间的距离，即称其为系统聚类法中的最短距离
  法（又称最近邻法）
  
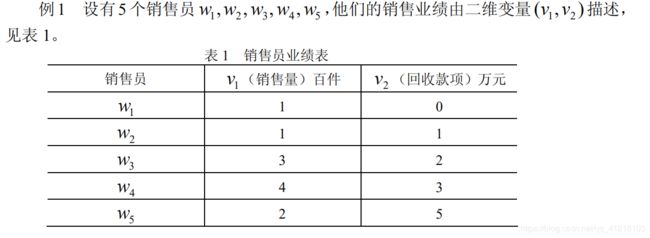
  解：

a=[1 0;1 1;3 2;4 3;2 5];
[m,n]=size(a);
d=zeros(m);
for i=1:m
    for j=i+1:m
        d(i,j)=mandist(a(i,:),a(j,:)');
        %求第一个矩阵的行向量与第二个矩阵的列向量之间的绝对值距离
   
    end
end
nd=nonzeros(d);
%去掉d中的零元素，非零元素按列排列

nd=union(nd,nd)
%去掉重复的非零元素

for i=1:m-1
    nd_min=min(nd);
    [row,col]=find(d==nd_min);
    tm=union(row,col);
    %将row,col归为一类
 
    tm=reshape(tm,1,length(tm));
    %将tm变为行向量
  
    fprintf('第%d次合成，平台高度为%d时的分类结果为：%s\n',... i,nd_min,int2str(tm)); 
 nd(find(nd==nd_min))=[];
  %删除已经归类的元素
 
 if length(nd)==0 
 break 
 end 
end





%使用MATLAB统计工具箱的相关命令：
y=pdist(a,'cityblock');
%求a的两两行向量见得绝对值距离

yc=squareform(y);
%变换成距离方阵

z=linkage(y);
%产生等级聚类树

[h,t]=dendrogram(z);
%画聚类图，由聚类图看出分为几类

m=3;
%m为划为m类
T=cluster(z,'maxclust',m)
%将对象划为m类

for i=1:m
    tm=find(T==i);
    %求第i类的对象
   
    tm=reshape(tm,1,length(tm));
    %变为行向量
    
    fprintf('第%d类的有%s\n',i,int2str(tm));
     %显示分类结果
end

• 有关聚类分析的MATLAB命令

1）pdist:计算欧式距离 , $Y=pdist(X{,}^{\prime }metri{c}^{\prime })$

Y=pdist(X)计算 $m\times n$ 矩阵 $X$（看作$m$ 个 $n$ 维行向量）中两两对象间的欧氏距离。
  对于有$m$ 个对象组成的数据集，共有$(m-1)\cdot m/2$个两两对象组合。 输出$Y$是包含距离信息的长度为$(m-1)\cdot m/2$的向量.
  $Y=pdist(X{,}^{\prime }metri{c}^{\prime })$中用${}^{\prime }metri{c}^{\prime }$指定的方法计算矩阵$X$中对象间的距离。${}^{\prime }metri{c}^{\prime }$可取下表中特征字符串值。

字符串	含 义
’Euclid’	欧氏距离（缺省）
’SEuclid’	标准欧氏距离
’Mahal’	马氏距离（Mahalanobis距离）
’CityBlock’	绝对值距离
’Minkowski’	闵氏距离（Minkowski距离）

注：$Y=pdist(X,’minkowski’,p)$用闵氏距离计算矩阵 $X$ 中对象间的距离。$p$ 为闵氏距离计算用到的指数值，缺省为2。

2）squareform:将计算出的欧氏距离转换成方阵，使矩阵中的元素$（i,j）$对应原始数据集中对象 $i$ 和 $j$ 间的距离。y=squareform(Y)

3）linkage：使用最短距离算法生成具层次结构的聚类树，Z=linkage(Y,‘method’)

输入矩阵 $Y$ 为 $pdist$ 函数输出的 $(m-1)\cdot m/2$ 维距离行向量。

使用由 ${}^{\prime }metho{d}^{\prime }$ 指定的算法计算生成聚类树。${}^{\prime }metho{d}^{\prime }$可取下表中特征字符串值。

输出矩阵 $Z$ 前两列为索引， $Z(1)$与 $Z(2)$ 是第 $Z(3)$ 个类中的元素

字符串	含 义
’single’	最短距离（缺省）
’complete’	最大距离
’average’	平均距离
’centroid’	重心距离
’ward’	离差平方和方法（Ward方法）

4）cluster，连接输出（linkage）中创建聚类。T=cluster(Z,cutoff,depth,flag)

参数depth指定了聚类数中的层数，进行不一致系数计算时要用到。不一致系数将聚类树中两对象的连接与相邻的连接进行比较。详细说明见函数inconsistent。当参数depth被指定时，cutoff通常作为不一致系数阈值。

参数flag重载参数cutoff的缺省含义。如flag为’inconsistent’，则cutoff作为不一致系数的阈值。如flag为’cluster’，则cutoff作为分类的最大数目

输出T为大小为m 的向量，它用数字对每个对象所属的类进行标识。为了找到包含在类i中的来自原始数据集的对象，可用 $find(T==i)$

$cutoff$ 为定义 $cluster$ 函数如何生成聚类的阈值

cutoff取值	含 义
0	cutoff作为不一致系数的阈值。不一致系数对聚类树中对象间的差异进行了量化。如果一个连接的不一致系数大于阈值，则cluster函数将其作为聚类分组的边界。
cutof >=2	cutoff作为包含在聚类树中的最大分类数

5 ) zsore(X):对数据矩阵进行标准化处理
处理方式：
$$\begin{gathered} x_{ij}=\frac{x_{ij}-{\overline{x}}_j}{s_j} \\ 其中:{\overline{x}}_j,s_j是矩阵X=(x_{ij}{)}_{m\times n}每一列的均值和标准差 \end{gathered}$$
6）H＝dendrogram(Z,P):画聚类树状图

$Z$ 是由 $linkage$ 产生的数据矩阵

7）T=clusterdata(X,cutoff)，clusterdata可以认为是pdist,linkage,cluster的综合，是对样本数据进行一次聚类。

将矩阵 $X$ 的数据分类。$X$ 为$m\times n$ 矩阵，被看作$m$ 个 $n$ 维行向量。它与以下几个命令等价：
$Y=pdist(X,’euclid’)$
$Z=linkage(Y,’single’)$
$T=cluster(Z,cutoff)$

8）cophenet:计算相干系数,c=cophenet(Z,Y)

  它是将 $Z$ 中的距离信息（由 $linkage()$ 函数产生）和 $Y$中的距离信息（由 $pdist()$函数产生）进行比较。Z为(m −1)×3矩阵，距离信息包含在第三列。Y是(m −1)⋅ m / 2维的行向量。
  例如，给定距离为Y的一组对象{1,2,L,m}，函数linkage()生成聚类树。cophenet()函数用来度量这种分类的失真程度，即由分类所确定的结构与数据间的拟合程度。
  输出值c为相干系数。对于要求很高的解，该值的幅度应非常接近1。它也可用来比较两种由不同算法所生成的分类解。

• R型聚类法
  1.变量相似性度量
  常用的变量相似性度量有两种。
  （1）相关系数
  
  (2）夹角余弦
  
  

2. 变量聚类法
   
   
   (数据在代码中)
   解：

a=[1 0 0 0 0 0 0 0 0 0 0 0 0 0
0.366 1 0 0 0 0 0 0 0 0 0 0 0 0
0.242 0.233 1 0 0 0 0 0 0 0 0 0 0 0
0.28 0.194 0.59 1 0 0 0 0 0 0 0 0 0 0
0.36 0.324 0.476 0.435 1 0 0 0 0 0 0 0 0 0
0.282 0.262 0.483 0.47 0.452 1 0 0 0 0 0 0 0 0
0.245 0.265 0.54 0.478 0.535 0.663 1 0 0 0 0 0 0 0
0.448 0.345 0.452 0.404 0.431 0.322 0.266 1 0 0 0 0 0 0
0.486 0.367 0.365 0.357 0.429 0.283 0.287 0.82 1 0 0 0 0 0
0.648 0.662 0.216 0.032 0.429 0.283 0.263 0.527 0.547 1 0 0 0 0
0.689 0.671 0.243 0.313 0.43 0.302 0.294 0.52 0.558 0.957 1 0 0 0
0.486 0.636 0.174 0.243 0.375 0.296 0.255 0.403 0.417 0.857 0.852 1 0 0
0.133 0.153 0.732 0.477 0.339 0.392 0.446 0.266 0.241 0.054 0.099 0.055 1 0 
0.376 0.252 0.676 0.581 0.441 0.447 0.44 0.424 0.372 0.363 0.376 0.321 0.627 1];
d=1-abs(a);
%将相关系数转化为距离
d=tril(d);
%提出d矩阵的下三角部分
b=nonzeros(d);
%去掉d中的0元素
b=b';
%转化为行向量
z=linkage(b,'complete');
 %按最长距离法聚类
dendrogram(z);
 %画聚类图,由图得到将变量划分为几类
 m=2;
 y=cluster(z,'maxclust',m);
 %将变量划分为m类
 for i=1:m
     find(y==i)'
     %显示第i类对应的变量标号
 end

 

• 聚类分析案例—我国各地区普通高等教育发展状况分析

a=[5.96 310 461 1557 931 319 44.36 2615 2.20 13631 
3.39 234 308 1035 498 161 35.02 3052 0.90 12665
2.35 157 229 713 295 109 38.40 3031 0.86 9385 
1.35 81 111 364 150 58 30.45 2699 1.22 7881
1.50 88 128 421 144 58 34.30 2808 0.54 7733 
1.67 86 120 370 153 58 33.53 2215 0.76 7480
1.17 63 93 296 117 44 35.22 2528 .58 8570
1.05 67 92 297 115 43 32.89 2835 0.66 7262 
0.95 64 94 287 102 39 31.54 3008 0.39 7786
0.69 39 71 205 61 24 34.50 2988 0.37 11355 
0.56 40 57 177 61 23 32.62 3149 0.55 7693 
0.57 58 64 181 57 22 32.95 3202 0.28 6805
0.71 42 62 190 66 26 28.13 2657 0.73 7282 
0.74 42 61 194 61 24 33.06 2618 0.47 6477 
0.86 42 71 204 66 26 29.94 2363 0.25 7704 
1.29 47 73 265 114 46 25.93 2060 0.37 5719
1.04 53 71 218 63 26 29.01 2099 0.29 7106 
0.85 53 65 218 76 30 25.63 2555 0.43 5580 
0.81 43 66 188 61 23 29.82 2313 0.31 5704
0.59 35 47 146 46 20 32.83 2488 0.33 5628 
0.66 36 40 130 44 19 28.55 1974 0.48 9106 
0.77 43 63 194 67 23 28.81 2515 0.34 4085 
0.70 33 51 165 47 18 27.34 2344 0.28 7928 
0.84 43 48 171 65 29 27.65 2032 0.32 5581 
1.69 26 45 137 75 33 12.10 810 1.00 14199 
0.55 32 46 130 44 17 28.41 2341 0.30 5714 
0.60 28 43 129 39 17 31.93 2146 0.24 5139 
1.39 48 62 208 77 34 22.70 1500 0.42 5377 
0.64 23 32 93 37 16 28.12 1469 0.34 5415 
1.48 38 46 151 63 30 17.87 1024 0.38 7368];
%*****************
%R型聚类分析
%*****************
r=corrcoef(a);
%求相关系数矩阵
d=1-r;
%进行数据变换，把相关数据转换为距离
d=tril(d);
%取矩阵的下三角元素
d=nonzeros(d);
%取出非0元素
d=d';
z=linkage(d,'average')
%按类平均法聚类
%类间相似度的计算选用类平均法。
dendrogram(z);
%画聚类图
T=cluster(z,'maxclust',6);
for i=1:6
    tm=find(T==i);
    tm=reshape(tm,1,length(tm));
    %变为行向量
    fprintf('第%d 类的有%s\n',i,int2str(tm)); 
    %显示分类结果
end



%*****************
%Q型聚类分析
%*****************
%样本间相似性采用欧氏距离度量，类间距离的计算选用类平均法
a(:,3:6)=[];
%删除数据矩阵的第3列到第6列
%因为第2，3,4,5,6指标相关性很强，所以使用变量2即可
a=zscore(a);
%数据标准化
y=pdist(a);
%求对象间的欧氏距离，每行是一个对象
z=linkage(y,'average');
%按类平均法聚类
dendrogram(z);
%画聚类图
for k=3:5
    fprintf('划分成%d类的结果如下：\n',k) 
 T=cluster(z,'maxclust',k); %把样本点划分成k类
 for i=1:k 
 tm=find(T==i); %求第i类的对象
 tm=reshape(tm,1,length(tm)); %变成行向量
 fprintf('第%d类的有%s\n',i,int2str(tm)); %显示分类结果
 end 
 if k==5 
 break 
 end 
 fprintf('**********************************\n'); 
end