MATLAB时间序列2（ARIMA,季节性序列及其预报）------2019/8/14

时间序列(时间序列模型只适合短时期预测，不适合长时期)

• 平稳时间序列
  
  
  1）平稳性检验及自协方差函数、自相关函数的估计
     1．平稳性 Daniel 检验
  
  

x0=[1.37 2.96 1.91 3.10 2.08 2.54 4.07 3.62 2.91 1.94 3.96 4.19 2.71 3.42 3.02 3.54 2.66 4.11 4.25 3.76];
x0=x0';
x0=x0(:)';
n=length(x0);
alpha=0.05
[xsort,ind]=sort(x0);
%按从小到大的次序排列数据
%[B,I] = sort(A,dim),B - 已排序数组;I - 排序索引

rt(ind)=1:n;
%计算秩

t=1:n;

qs=1-6/(n*(n^2-1))*sum((t-rt).^2)
%计算qs的值，

t=qs*sqrt(n-2)/sqrt(1-qs^2)
%计算 t 统计量的值

t_0=tinv(1-alpha/2,n-2)
%计算上 alpha/2的分位点
%若t>t_0,则拒绝H0，认为序列是非平稳的，若qs>0,则序列有上升趋势

2. ARMA 时间序列及其特性
   $$ARMA时间序列=\{\begin{array}{l}AR模型，即自回归序列\\ MA序列，即滑动平均序列\\ ARMA序列，即自回归滑动平均序列\end{array}$$
   理论描述没懂
   

（性质太多，不写了。看书吧《数学建模算法与应用》p507）

• ARIMA 序列与季节性序列
  
  
   设 $X_t$ 是$ARIMA(p,d,q)$ 序列，则当 $p=0$ 时，称为 $IMA(d,q)$ 序列；当 $q=0$时，称为$ARI(p,d)$ 序列。
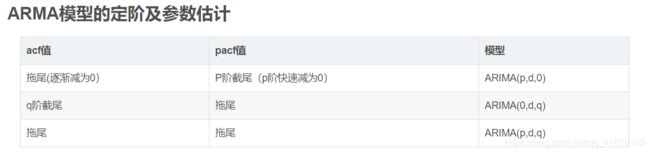
  系数拖着长长的尾巴，就是拖尾，值是慢慢减少的;
  系数是突然收敛到临界值水平范围内的，就是截尾，值突然变的很小。
  截尾和拖尾：$x_{i+1}=e^{-m{x}_1}$表明误差越来越小。
  

AR模型：	自相关系数拖尾，偏自相关系数截尾
MA模型：	自相关系数截尾，偏自相关函数拖尾
ARMA模型：	自相关函数和偏自相关函数均拖尾

解：

a=[17.0 16.6 16.3 16.1 17.1 16.9 16.8 17.4 17.1 17.0 
16.7 17.4 17.2 17.4 17.4 17.0 17.3 17.2 17.4 16.8 
17.1 17.4 17.4 17.5 17.4 17.6 17.4 17.3 17.0 17.8 
17.5 18.1 17.5 17.4 17.4 17.1 17.6 17.7 17.4 17.8 
17.6 17.5 16.5 17.8 17.3 17.3 17.1 17.4 16.9 17.3 
17.6 16.9 16.7 16.8 16.8 17.2 16.8 17.6 17.2 16.6 
17.1 16.9 16.6 18.0 17.2 17.3 17.0 16.9 17.3 16.8 
17.3 17.4 17.7 16.8 16.9 17.0 16.9 17.0 16.6 16.7 
16.8 16.7 16.4 16.5 16.4 16.6 16.5 16.7 16.4 16.4 
16.2 16.4 16.3 16.4 17.0 16.9 17.1 17.1 16.7 16.9 
16.5 17.2 16.4 17.0 17.0 16.7 16.2 16.6 16.9 16.5 
16.6 16.6 17.0 17.1 17.1 16.7 16.8 16.3 16.6 16.8 
16.9 17.1 16.8 17.0 17.2 17.3 17.2 17.3 17.2 17.2 
17.5 16.9 16.9 16.9 17.0 16.5 16.7 16.8 16.7 16.7 
16.6 16.5 17.0 16.7 16.7 16.9 17.4 17.1 17.0 16.8 
17.2 17.2 17.4 17.2 16.9 16.8 17.0 17.4 17.2 17.2 
17.1 17.1 17.1 17.4 17.2 16.9 16.9 17.0 16.7 16.9 
17.3 17.8 17.8 17.6 17.5 17.0 16.9 17.1 17.2 17.4 
17.5 17.9 17.0 17.0 17.0 17.2 17.3 17.4 17.4 17.0 
18.0 18.2 17.6 17.8 17.7 17.2 17.4 0 0 0];
a=nonzeros(a');
%按照原来数据的顺序去掉零元素
r11=autocorr(a);
%计算自相关系数
r12=parcorr(a);
%计算偏相关函数
figure
subplot(211),autocorr(a);
subplot(212),parcorr(a);
%将原始数据的自相关与偏自相关数据画在一个图上
%由于r11为正，即不是被负指数控制的，所以计算一阶差分:
da=diff(a);
r21=autocorr(da);
%计算自相关系数
r22=parcorr(da);
%计算偏相关函数
adf=adftest(da);
%若adf==1，则表明是平稳时间序列。
figure
subplot(211),autocorr(da);
subplot(212),parcorr(da);
%将一阶查分后的自相关与偏自相关数据画在一个图上，由图可以明显看出数据变成平稳数列。
n=length(da);
%计算差分后的数据个数
%由图形可看出
k=0;
  for i = 0:3
    for j = 0:3 %0:L,L的值不确定 
        if i == 0 & j == 0
            continue
        elseif i == 0
            ToEstMd = arima('MALags',1:j,'Constant',0); %指定模型的结构
        elseif j == 0
            ToEstMd = arima('ARLags',1:i,'Constant',0); %指定模型的结构
        else
            ToEstMd = arima('ARLags',1:i,'MALags',1:j,'Constant',0); %指定模型的结构
        end
        k = k + 1;
        R(k) = i;
        M(k) = j;
        [EstMd,EstParamCov,LogL,info] = estimate(ToEstMd,da);
        %模型拟合,估计模型参数
        numParams = sum(any(EstParamCov));
        %计算拟合参数的个数
        [aic(k),bic(k)] = aicbic(LogL,numParams,n);
    end
end
fprintf('R,M,AIC,BIC的对应值如下\n%f');%显示计算结果
check  = [R',M',aic',bic'];
%模型验证：
 res=infer(EstMd,da);
%求条件方差，条件方差增加，波动性增加
figure
subplot(2,2,1)
plot(res./sqrt(EstMd.Variance))
%画出标准化残差
title('Standardized Residuals')
subplot(2,2,2),qqplot(res)
%QQ图中残差基本完全落在45°线上即为符合正态性假设。否则模型可能出现错误.
subplot(2,2,3),autocorr(res)
subplot(2,2,4),parcorr(res)


%定阶：
%由差分后的自相关图与偏自相关数据图可知：
%自相关系数在滞后1阶后就快速的减为0，偏自相关系数同自相关系数
%所以，p=1,q=1

%模型预测：
p=input('输入阶数P=');
q=input('输入阶数q=');
ToEstMd=arima('ARLags',1:p,'MALags',1:q,'Constant',0); 
%指定模型的结构
 [EstMd,EstParamCov,LogL,info] = estimate(ToEstMd,da);
 %模型拟合,估计模型参数
%  dx_forest=forecast(EstMd,10,'Y0',da);
 %预测确定的模型输出
 dx_forest=forecast(EstMd,10,'Y0',da);
 %dx_forest预测的响应,'10'表示求10步预测值
 x_forest=a(end)+cumsum(dx_forest)
 %计算原始数据的10步预测值
%画图：
figure
h4 = plot(a,'b');
 hold on
 h5 = plot(length(a)+1:length(a)+10,x_forest,'r','LineWidth',2);
 hold off

• 季节性序列及其预报
    由季节性因素或其它周期因素引起的周期性变化的时间序列，我们称为季节性时间序列，相应的模型为季节性模型。
  
  
  
  
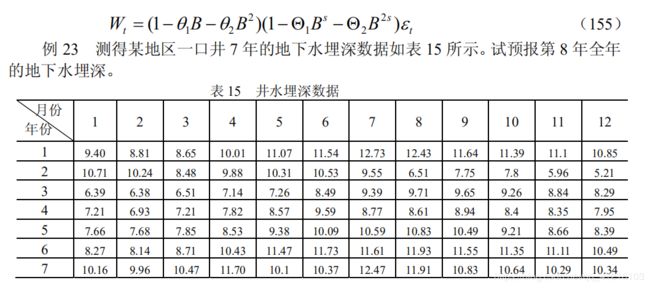
  解：

water=[9.40 8.81 8.65 10.01 11.07 11.54 12.73 12.43 11.64 11.39 11.1 10.85 
10.71 10.24 8.48 9.88 10.31 10.53 9.55 6.51 7.75 7.8 5.96 5.21 
6.39 6.38 6.51 7.14 7.26 8.49 9.39 9.71 9.65 9.26 8.84 8.29 
7.21 6.93 7.21 7.82 8.57 9.59 8.77 8.61 8.94 8.4 8.35 7.95 
7.66 7.68 7.85 8.53 9.38 10.09 10.59 10.83 10.49 9.21 8.66 8.39 
8.27 8.14 8.71 10.43 11.47 11.73 11.61 11.93 11.55 11.35 11.11 10.49 
10.16 9.96 10.47 11.70 10.1 10.37 12.47 11.91 10.83 10.64 10.29 10.34];
water=water';
x=water(:)';
%water(:)为将water中的数据转化为一列数据
r11=autocorr(x);
%计算自相关系数
r12=parcorr(x);
%计算偏相关函数
figure
subplot(211),autocorr(r11);
subplot(212),parcorr(r12);
s=12;
%地下水按照12个月的季节性变化
n=12;
%预报数据的个数
m1=length(x);
%原始数据的个数
for i=s+1:m1
    y(i-s)=x(i)-x(i-s);
    %周期差分：相邻两个年份同一个月分的地下水位的差
end
m2=length(y);
%周期差分后数据的个数
w=diff(y);
%消除趋势性的差分运算
r21=autocorr(w);
%计算自相关系数
r22=parcorr(w);
%计算偏相关函数
adf=adftest(w);
%若adf==1，则表明是平稳时间序列。
figure
subplot(211),autocorr(r21);
subplot(212),parcorr(r22);
m3=length(w);
%计算最终差分后数据的个数
k=0;
for i = 0:3
    for j = 0:3 %0:L,L的值不确定 
        if i == 0 & j == 0
            continue
        elseif i == 0
            ToEstMd = arima('MALags',1:j,'Constant',0); %指定模型的结构
        elseif j == 0
            ToEstMd = arima('ARLags',1:i,'Constant',0); %指定模型的结构
        else
            ToEstMd = arima('ARLags',1:i,'MALags',1:j,'Constant',0); %指定模型的结构
        end
        k = k + 1;
        R(k) = i;
        M(k) = j;
        [EstMd,EstParamCov,LogL,info] = estimate(ToEstMd,w');
        %模型拟合,估计模型参数
        numParams = sum(any(EstParamCov));
        %计算拟合参数的个数
        [aic(k),bic(k)] = aicbic(LogL,numParams,m2);
    end
end
fprintf('R,M,AIC,BIC的对应值如下\n%f');%显示计算结果
check  = [R',M',aic',bic']

%模型验证：
 res=infer(EstMd,w');
%求条件方差，条件方差增加，波动性增加
figure
subplot(2,2,1)
plot(res./sqrt(EstMd.Variance));
%画出标准化残差
title('Standardized Residuals');
subplot(2,2,2),qqplot(res);
%QQ图中残差基本完全落在45°线上即为符合正态性假设。否则模型可能出现错误.
subplot(2,2,3),autocorr(res);
subplot(2,2,4),parcorr(res);


%定阶：
%由差分后的由差分后的自相关图与偏自相关数据图可知：
%自相关系数在滞后1阶后就快速的减为0，偏自相关系数同自相关系数
%所以，p=1,q=1

%模型预测：
p=input('输入阶数P=');
q=input('输入阶数q=');
ToEstMd=arima('ARLags',1:p,'MALags',1:q,'Constant',0); 
%指定模型的结构
 [EstMd,EstParamCov,LogL,info] = estimate(ToEstMd,w');
 %模型拟合,估计模型参数
 dy_forest=forecast(EstMd,n,'Y0',w');
 %预测确定的模型输出,注意已知数据应为列向量，所以用w'.
 yhat=y(m2)+cumsum(dy_forest);
 %求一阶差分的还原值
 yhat=yhat';
 for j=1:n
     x(m1+j)=yhat(j)+x(m1+j-s);
     %求x的预测值
 end
 what=x(m1+1:end);
 %截取n个预报值
 %画图：
 figure
 h4 = plot(x,'b');
 hold on
 h5 = plot(length(x)+1:length(x)+n,what,'r','LineWidth',2);
 hold off