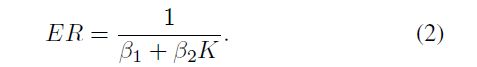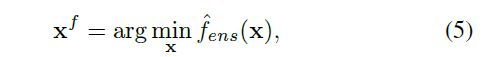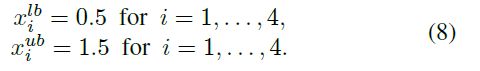数据驱动进化优化(data-driven evolutionary optimization)
Data-Driven Evolutionary Optimization: An Overview and Case Studies
论文链接:
https://ieeexplore.ieee.org/document/8456559
本文介绍了数据驱动进化优化的综述,对论文的翻译和总结
目录
1:中英对照翻译
I. INTRODUCTION
II. DATA-DRIVEN EVOLUTIONARY OPTIMIZATION
A. Data Collection
B. Off-line and On-line Data-Driven Optimization Methodolo-gies
C On-line Data-Driven Optimization Methodologies:
III. CASE STUDIES
A. Off-line Small Data-Driven Blast Furnace Optimization
B. Off-line Big Data-Driven Trauma System Design Optimization
C. Off-line Small Data-Driven Optimization of Fused Magnesium Furnaces
D. On-line Small Data-Driven Optimization of Airfoil Design
E. On-line Small Data-Driven Optimization of An Air Intake Ventilation System
IV. CHALLENGES AND PROMISES
A. On-line Data-Driven Optimization
B. Off-line Data-Driven Optimization
V. CONCLUSIONS
2:总结:
1 什么是EAs?
2 什么叫做数据驱动优化?
3 数学优化vs数据驱动进化优化
4 数据驱动存在什么问题?
5 数据的类型
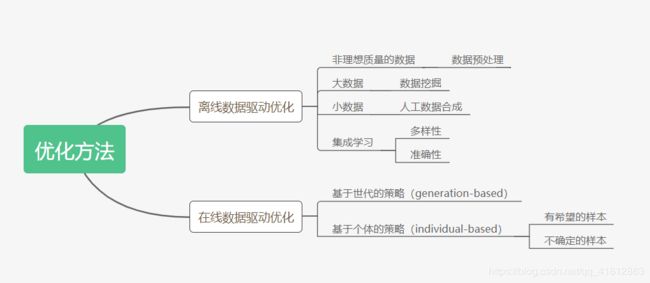
6 优化方法的类型
1:中英对照翻译
Abstract—Most evolutionary optimization algorithms assume that the evaluation of the objective and constraint functions is straightforward. In solving many real-world optimization problems, however, such objective functions may not exist. In-stead, computationally expensive numerical simulations or costly physical experiments must be performed for fitness evaluations. In more extreme cases, only historical data are available for per-forming optimization and no new data can be generated during optimization. Solving evolutionary optimization problems driven by data collected in simulations, physical experiments, production processes, or daily life are termed data-driven evolutionary optimization. In this paper, we provide a taxonomy of different data driven evolutionary optimization problems, discuss main challenges in data-driven evolutionary optimization with respect to the nature and amount of data, and the availability of new data during optimization. Real-world application examples are given to illustrate different model management strategies for different categories of data-driven optimization problems.
摘要——大多数进化优化算法假设目标函数和约束函数的评估是简明直接的。然而,在解决许多实际优化问题时,这样的目标函数可能并不存在。事实上,我们必须进行昂贵的计算数值模拟或昂贵的物理实验来进行适应度评估。在更极端的情况下,只有历史数据可用于优化,在优化期间不能生成新数据。通过模拟、物理实验、生产过程或日常生活中收集的数据来解决进化优化问题称为数据驱动的进化优化。在本文中,我们提供了不同数据驱动进化优化问题的分类,讨论了数据驱动进化优化中的主要挑战,这些挑战涉及数据的性质和数量,以及优化过程中新数据的可用性。通过实例说明了不同类型数据驱动优化问题的模型管理策略。
Index Terms—Data-driven optimization, evolutionary algorithms, surrogate, model management, data science, machine learning
索引术语——数据驱动的优化、进化算法、代理、模型管理、数据科学、机器学习
I. INTRODUCTION
Many real-world optimization problems are difficult to solve in that they are non-convex or multi-modal, large-scale, highly
constrained, multi-objective, and subject to a large amount of uncertainties. Furthermore, the formulation of the optimization problem itself can be challenging, requiring a number of iterations between the experts of the application area and computer scientists to specify the appropriate representation, objectives, constraints and decision variables [1]–[3].
现实生活中,许多优化问题由于具有非凸或多模态、大规模、高约束、多目标、限制条件不确定性大等特点而难以求解。此外,优化问题的公式本身是具有挑战性的,需要在应用领域的专家和计算机科学家之间进行多次循环反复(iterations),以指定适当的表示、目标、约束和决策变量[1][3]。
This research was supported in part by an EPSRC grant (No. EP/M017869/1), in part by the National Natural Science Foundation of China (No. 61590922), and in part by the Finland Distinguished Professor Programme funded by the Finnish Funding Agency for Innovation (Tekes). The research is related to the thematic research area on Decision Analytics (DEMO) at the University of Jyv¨askyl¨a. (Corresponding author: Yaochu Jin)
Y. Jin is with the Department of Computer Science, University of Surrey, Guildford GU2 7XH, U.K. He is also affiliated with the Department of Computer Science and Technology, Taiyuan University of Science and Tech-nology, Taiyuan 030024, China, and the State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang, China (e-mail: [email protected]).
这项研究一部分得到了EPSRC的资助,部分由中国国家自然科学基金资助,部分由芬兰创新资助局资助。本研究与J大学的决策分析主题研究领域(DEMO)相关(作者:金)金是英国萨里大学计算机科学系的,他也隶属于中国太原理工大学计算机科学与技术系,和中国东北大学过程工业综合自动化国家重点实验室。(电子邮件:[email protected])。
H. Wang is with School of Artificial Intelligence, Xidian University, Xi’an 710071, China. This work was done when she was with the Department of Computer Science, University of Surrey, Guildford, GU2 7XH, UK. (e-mail: [email protected]).
王晗丁就职于中国西安电子科技大学人工智能学院。这项工作是她在英国吉尔福德萨里大学计算机科学系完成的。(电子邮件:[email protected])。
T. Chugh is with the Department of Computer Science, University of Exeter, United Kingdom, U.K. (email: [email protected]).
D. Guo is with the State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang, China (email: [email protected]).
K. Miettinen is with the University of Jyvaskyla, Faculty of Information Technology, P.O. Box 35 (Agora), FI-40014 University of Jyvaskyla, Finland (email: [email protected])
以上人物介绍翻译略
Over the past decades, evolutionary algorithms (EAs) have become a popular tool for optimization [4], [5]. Most existing research on EAs is based on an implicit assumption that evaluating the objectives and constraints of candidate solutions is easy and cheap. However, such cheap functions do not exist for many real-world optimization problems. Instead, evaluations of the objectives and / or constraints can be performed only based on data, collected either from physical experiments, numerical simulations, or daily life. Such optimization problems can be called data-driven optimization problems [6]. In addition to the challenges coming from the optimization, data-driven optimization may also be subject to difficulties resulting from the characteristics of data. For example, the data may be distributed, noisy, heterogeneous, or dynamic (streaming data), and the amount of data may be big or small, imposing different challenges to the data-driven optimization algorithm.
在过去的几十年里,进化算法(EAs)已经成为优化的流行工具[4],[5]。大多数现有的关于EAs的研究是基于一个隐含的假设,即评估候选解决方案的目标和约束是简单和廉价的。然而,这种廉价的函数并不存在于许多实际的优化问题中。相反,对目标和/或约束条件的评估只能基于从物理实验、数值模拟或日常生活中收集的数据。这种优化问题可以称为数据驱动优化问题[6]。除了优化带来的挑战之外,数据驱动的优化也可能因为数据的特性而遇到困难。例如,数据可能是分布式的、嘈杂的、异构的或动态的(流数据),数据量可能大或小,给数据驱动的优化算法带来不同的挑战。
In some data-driven optimization problems, evaluations of the objective or constraint functions involve time- or resource-intensive physical experiments or numerical simulations ( often referred to as simulation-based optimization). For example, a single function evaluation based on computational fluid dynamic (CFD) simulations could take from minutes to hours [1]. To reduce the computational cost, surrogate models (also known as meta-models [7]) have been widely used in EAs, which are known as surrogate-assisted evolutionary algorithms (SAEAs) [8]. SAEAs perform a limited number of real function evaluations and only a small amount of data is available for training surrogate models to approximate the objective and / or constraint functions [9], [10]. Most machine learning models, including polynomial regression [11], Krig-ing model [12], [13], artificial neural networks (ANN) [14]–[16], and radial basis function networks (RBFN) [17]–[20] have been employed in SAEAs. With limited training data, approximation errors of surrogate models are inevitable, which may mislead the evolutionary search. However, as shown in [21], [22], an EA may benefit from the approximation errors introduced by surrogates, and therefore, it is essential in SAEAs to make full use of the limited data.
在一些数据驱动的优化问题中,对目标或约束函数的评估涉及到时间或资源密集型的物理实验或数值模拟(通常称为基于模拟的优化)。例如,一个基于计算流体动力学(CFD)模拟的单一功能评估可能需要几分钟到几个小时[1]。为了降低计算成本,代理模型(也称为元模型[7])在EAs中被广泛使用,称为替代辅助进化算法(SAEAs)[8]。SAEAs执行有限数量的实函数评估,只有少量的数据可用来训练替代模型来近似目标和/或约束函数[9],[10]。大多数机器学习模型,包括多项式回归[11]、Kriging模型[12]、[13]、人工神经网络(ANN)[14][16]、径向基函数网络(RBFN)[17][20]已被用于SAEAs。在训练数据有限的情况下,替代模型的近似误差是不可避免的,这可能会误导进化搜索。然而,如[21]、[22]所示,EA可能受益于代理引入的近似误差,因此,SAEAs必须充分利用有限的数据。
In contrast to the above situation in which collecting data is expensive and only a small amount of data is available, there are also situations in which function evaluations must be done on the basis a large amount of data. The hardness brought by data to data-driven EAs is twofold. Firstly, acquiring and processing data for function evaluations increase the resource and computational cost, especially when there is an abundant amount of data [23]. For example, a single function evaluation of the trauma system design problem [6] needs to process 40,000 emergency incident records. Secondly, the function evaluations based on data are the approximation of the exact function evaluations, because the available data is usually not of ideal quality. Incomplete [24], imbalanced [25], [26], and noisy [27], [28] data bring errors to function evaluations of data-driven EAs, which may mislead the search.
与上述收集数据昂贵且只有少量数据的情况相比,还有一些情况需要在大量数据的基础上进行功能评估。数据给数据驱动的EAs带来的困难是双重的。首先,函数评估数据的获取和处理增加了资源和计算成本,特别是在[23]数据量丰富的情况下。例如,创伤系统设计问题[6]的单一功能评估需要处理40000个紧急事件记录。其次,基于数据的函数评价是精确函数评价的近似值,因为可用的数据通常质量不理想。[24]不完整,[25],[26]不平衡,[27],[28]数据有噪声会给数据驱动的EAs的功能评估带来错误,可能会误导搜索。
This paper aims to provide an overview of recent advances in the emerging research area of data-driven evolutionary optimization. Section II provides more detailed background about data-driven optimization, including a categorization with respect to the nature of the data, whether new data can be collected during optimization, and the surrogate management strategies used in data-driven optimization. Five case studies of real-world data-driven optimization problems are presented in Section III, representing situations where the amount of data is either small or big, and new data is or is not allowed to be generated during optimization. Open issues for future work in data-driven optimization are discussed in detail in Section IV, and Section V concludes the paper.
本文旨在提供数据驱动进化优化新兴研究领域的最新进展综述。第二节提供了关于数据驱动优化的更详细的背景知识,包括关于数据性质的分类、优化期间是否可以收集新数据,以及在数据驱动优化中使用的代理管理策略。第三节给出了现实世界数据驱动优化问题的五个案例研究,描述了在优化过程中数据量大或小以及新数据被允许或不被允许生成的情况。第四节详细讨论了未来数据驱动优化工作中有待解决的问题,第五节对本文进行总结。
II. DATA-DRIVEN EVOLUTIONARY OPTIMIZATION
Generally speaking, EAs begin with a randomly initialized parent population. In each iteration of EAs, an offspring population is generated via a number of variation operators, crossover and mutation, for instance. All solutions in the offspring population will then be evaluated to calculate their fitness value and assess their feasibility. Then, the new parent population for the next iteration is selected from the offspring population or a combination of the parent and offspring populations.
一般来说,EAs从一个随机初始化的父种群开始。在EAs的每次迭代中,通过大量的变异操作,例如交叉和突变,产生一个后代种群。所有的解决方案将在后代群体中进行评估,以计算其适合度值并评估其可行性。然后,从子种群或父种群和子种群的组合中选择下一个迭代的新父种群。
Fig. 1 presents the three main disciplines involved in data-driven evolutionary optimization, namely, evolutionary computation (including other population-based meta-heuristic search methods), machine learning (including all learning techniques), and data science. While the traditional chal-lenges remain to be handled in each discipline, new research questions may arise when machine learning models are built for efficiently guiding the evolutionary search given various amounts and types of data.
图1展示了涉及数据驱动进化优化的三个主要学科,即进化计算(包括其他基于种群的元启发式搜索方法)、机器学习(包括所有学习技术)和数据科学。虽然每个学科都需要处理传统的长时间问题,但是当建立机器学习模型来有效地指导给定不同数量和类型的数据的进化搜索时,新的研究问题可能会出现。
Although they are widely used, surrogates in data-driven evolutionary optimization have a much broader sense than in surrogate-assisted evolutionary optimization. For example, the ”surrogate” in the case study in Section III.B is more a way of reducing the amount of data to be used in fitness evaluations rather than an explicit surrogate model, where an update of the ”surrogate” is to adaptively find the right number of data clusters.
虽然代理在数据驱动的进化优化中得到了广泛的应用,但它在数据驱动的进化优化中比在代理辅助的进化优化中具有更广泛的意义。以第三节案例研究中的代理为例。B更多的是一种减少在适应度评估中使用的数据量的方法,而不是显式代理模型,其中代理模型的更新是自适应地找到正确数量的数据集群。
It should also be emphasized that data or domain knowledge can be utilized to speed up the evolutionary search almost in every component of an evolutionary algorithm, as illustrated in Fig. 2. For example, history data can be used to determine the most effective and compact representation of a very large scale complex problem [29]. We also want to note that domain knowledge about the problem structure or information about the search performance acquired in the optimization process can be incorporated or re-used in EAs to enhance the evolutionary search performance. These techniques are usually known as knowledge incorporation in EAs [30].
还需要强调的是,数据或领域知识几乎可以在进化算法的每个组件中用于加速进化搜索,如图2所示。例如,历史数据可以用来确定一个非常大的复杂问题的最有效和紧凑的表示[29]。我们还想指出,在优化过程中获得的关于问题结构的领域知识或关于搜索性能的信息可以在EAs中合并或重用,以增强进化搜索性能。这些技术通常被称为EAs中的知识整合[30]。
In the following, we discuss in detail the challenges in data collection and surrogate construction arising from data-driven optimization.
在下面,我们将详细讨论数据驱动优化在数据收集和代理构造方面遇到的挑战。
A. Data Collection
Different data-driven optimization problems may have com-pletely different data resources and data collection methods. Roughly speaking, data can be classified into two large types: direct and indirect data, consequently resulting in two different types of surrogate modelling and management strategies, as shown in Fig. 1.
不同的数据驱动优化问题可能有完全不同的数据资源和数据收集方法 粗略地讲,数据可以分为两大类:直接数据和间接数据,因此产生了两种不同类型的代理建模和管理策略,如图1所示
One type of data in data-driven optimization is directly collected from computer simulations or physical exper-iments, in which case each data item is composed of the decision variables, corresponding objective and / or constraint values, as shown in the bottom right panel of Fig. 1. This type of data can be directly used to train surrogate models to approximate the objective and / or constraint functions, which has been the main focus in SAEAs [9], [10]. We call surrogate models built from direct data Type I surrogate models. Note that during the optimization, EAs may or may not be allowed to actively sample new data.
在数据驱动优化中,有一类数据是直接从计算机模拟或物理实验中收集的,在这种情况下,每个数据项由决策变量、相应的目标值和/或约束值组成,如图1右下方面板所示。这种类型的数据可以直接用于训练替代模型来近似目标和/或约束函数,这一直是SAEAs的主要关注点[9],[10]。我们将从直接数据中构建的代理模型称为I型代理模型。注意,在优化期间,EAs可能被允许也可能不被允许主动取样新数据。
The second type of data is called indirect data. For example, some of the objective and constraint functions in the trauma system design problem [6] can only be cal-culated using emergency incident records. In this case, the data are not presented in the form of decision variables and objective values. However, objective and constraint values can be calculated using the data, which are then further used for training surrogates. We term surrogate models based on indirect data Type II surrogate models. In contrast to direct data, it is usually less likely, if not impossible, for EAs to actively sample new data during optimization.
第二种类型的数据称为间接数据。例如,创伤系统设计问题[6]中的一些目标和约束函数只能使用紧急事件记录来计算。在这种情况下,数据没有以决策变量和客观值的形式呈现。然而,可以利用这些数据计算出目标值和约束值,然后进一步用于培训代理,我们将基于间接数据的代理模型称为II型代理模型。与直接数据相比,在优化过程中,EAs不太可能(如果不是不可能的话)主动取样新数据。
In addition to the difference in the presentation form of the data, other properties related to data are also essential for data-driven evolutionary optimization, including the cost of collecting data, whether new data is allowed to be collected during the optimization, and whether data collection can be actively controlled by the EA. Last but not the least, data of multiple fidelity can also be made available for both data types [31]–[34].
除了数据的表现形式的差异,其他相关数据的属性对数据驱动进化优化也是必不可少的,包括收集数据的成本,是否允许在优化期间收集新数据,以及数据收集是否可以由EA主动控制。以及,两种数据类型都可以使用多重保真度的数据等[31][34]。
In the following, we divide data-driven EAs into off-line and on-line methodologies, according to whether new data is allowed to be actively generated by the EA [6].
下面,我们根据EA[6]是否允许主动生成新数据,将数据驱动的EAs分为离线和在线方法。
B. Off-line and On-line Data-Driven Optimization Methodolo-gies
Off-line Data-Driven Optimization Methodologies: In off-line data-driven EAs, no new data can be actively generated during the optimization process [35], presenting serious challenges to surrogate management. Since no new data can be actively generated, off-line data-driven EAs focus on building surrogate models based on the given data to explore the search space. In this case, the surrogate management strategy heavily relies on the quality and amount of the available data.
离线数据驱动的优化方法:在离线数据驱动的EAs中,在优化过程[35]期间不能主动生成新的数据,对代理管理提出了严峻的挑战。由于不能主动生成新数据,脱机数据驱动的EAs关注于基于给定数据构建代理模型,以探索搜索空间。在这种情况下,代理管理策略严重依赖于可用数据的质量和数量。
Data with non-ideal quality: Real-world data can be incomplete [24], imbalanced [36], or noisy [27], [28]. Consequently, construction of surrogates must take into account these challenges and nevertheless, the resulting surrogates are subject to large approximation errors that may mislead the evolutionary search.
非理想质量的数据:真实世界的数据可以是不完整的[24],不平衡的[36],或有噪声的[27],[28]。因此,代理的构建必须考虑到这些挑战,即使如此,所产生的代理依旧会受到很大的近似误差,可能会误导进化的搜索。
Big data: In off-line data-driven optimization, the amount of the data can be huge, which results in prohibitively large computational cost for data processing and fitness calculation based on the data [23]. The computational cost of building surrogate models also dramatically in-creases with the increasing amount of the training data.
大数据:在离线数据驱动优化中,数据量可能非常大,这导致基于数据进行数据处理和适应度计算的计算成本非常高[23]。建立代理模型的计算成本也会随着训练数据量的增加而急剧增加。
Small data: Opposite to big data, the amount of available data may be extremely small due to the limited time and resource available for collecting data. Data paucity is often attributed to the fact that numerical simulations of complex systems are computationally very intensive, or physical experiments are very costly. A direct challenge resulting from small data is the poor quality of the surrogates, in particular for off-line data-driven optimization where no new data can be generated during optimization.
小数据:相对于大数据,由于收集数据的时间和资源有限,可用的数据量可能极小。数据的缺乏通常归因于复杂系统的数值模拟计算非常密集,或物理实验非常昂贵。小数据带来的一个直接挑战是代理的质量差,特别是对于脱机数据驱动优化,在优化期间不能生成新数据。
Note, however, that a standard criterion to quantify big data and small data still lacks [37], as a sensible definition may depend on the problem and the computational resources available for solving the problem at hand.
但是请注意,如今仍然缺乏量化大数据和小数据的标准[37],因为一个合理的定义依赖于问题和用于解决当前问题的可用计算资源。
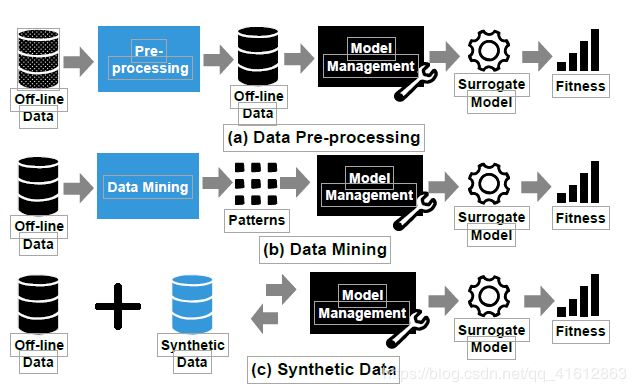
Because of the above-mentioned challenges, not many off-line data-driven EAs have been proposed. The strategies for handling data in off-line data-driven EAs can be divided into three categories: data pre-processing, data mining, and synthetic data generation, as shown in Fig. 3.
由于上述的挑战,并没有很多离线数据驱动的EAs被提出。离线数据驱动的EAs处理数据的策略可以分为三类:数据预处理、数据挖掘和人工数据合成,如图3所示。
1) Data pre-processing: For data with non-ideal quality, pre-processing is necessary. As highlighted in Fig. 3 (a), off-line data must be pre-processed before they are used to train surrogates to enhance the performance of data-driven EAs. Taking the blast furnace problem in [38] as an example, which is a many-objective optimization problem, the available data collected from production is very noisy. Before building surrogates to approximate the objective functions, a local regression smoothing [39] is used to reduce the noise in the off-line data. Then, Kriging models are built to assist the reference vector guided evolutionary algorithm (RVEA)[40].
数据预处理:对于质量不理想的数据,需要进行预处理。正如图3 (a)中突出显示的那样,必须对脱机数据进行预处理,然后再对其进行训练代理,以提高数据驱动EAs的性能。以高炉问题[38]为例,这是一个多目标优化问题,生产中收集的可用数据噪声很大。在建立代理来近似目标函数之前,使用一个局部回归平滑[39]来降低离线数据中的噪声。然后,建立克里格模型来辅助参考向量引导进化算法(RVEA)[40]。
2)Data mining: When data-driven EAs involve big data, the computational cost may be unaffordable. Since big data often has redundancy [41], existing data mining techniques can be employed to capture the main patterns in the data. As shown in Fig. 3 (b), the data-driven EA is based on the obtained patterns rather than the original data to reduce the computational cost. In the trauma system design problem [6], there are 40,000 records of emergency incidents and a clustering technique is adopted to mine patterns from the data before building surrogate models.
2)数据挖掘:当数据驱动的EAs涉及大数据时,计算成本可能难以承受。由于大数据通常具有冗余[41],现有的数据挖掘技术可以用于捕获数据中的主要成分。如图3 (b)所示,数据驱动的EA是基于获得模式(obtained patterns),而不是原始数据,以减少计算成本。在创伤系统设计问题[6]中,有40000个紧急事件记录,在构建替代模型之前,我们采用聚类技术从数据中挖掘成分。
3)Synthetic data generation: When the quantity of the data is small and no new data is allowed to be generated, it is extremely challenging to obtain high-quality surro-gate models. To address this problem, synthetic data can be generated in addition to the off-line data, as shown in Fig. 3 (c). This idea has shown to be helpful in data-driven optimization of the fused magnesium furnace optimization problem [42], where the size of available data is extremely small and it is impossible to obtain new data during optimization. In the proposed algorithm in [42], a low-order polynomial model is employed to replace the true objective function to generate synthetic data for model management during optimization.
3)人工数据合成:在数据量较小且不允许生成新数据的情况下,获取高质量的代理模型极具挑战性。为了解决这个问题,可以在离线下合成人工数据,如图3所示(c)。这个想法已经被熔镁炉优化问题[42]证明是有用的数据驱动的优化,可用数据的规模非常小,在优化中无法获得新的数据。在[42]中提出的优化算法中,采用低阶多项式模型代替真实目标函数生成人工数据,用于优化过程中的模型管理。
Off-line data-driven EAs are of practical significance in industrial optimization. However, it is hard to validate the obtained optimal solutions before they are really implemented.
离线数据驱动的EAs在产业优化中具有重要的现实意义。然而,在得到最优解之前,很难验证这一切。
C On-line Data-Driven Optimization Methodologies:
Compared with off-line data-driven EAs, on-line data-driven EAs can make additional data available for managing the surrogate models, as shown in Fig. 4. Thus, on-line data-driven EAs are more flexible than off-line data-driven EAs, which offers many more opportunities to improve the performance of the algorithm than off-line data-driven EAs.
与离线数据驱动的EAs相比,在线数据驱动的EAs可以提供更多的数据来管理替代模型,如图4所示。因此,在线数据驱动的EAs比离线数据驱动的EAs更灵活,这比离线数据驱动的EAs提供了更多的机会来提高算法的性能。
Note that off-line data-driven EAs can be seen as a special case of on-line data-driven EAs in that usually, a certain amount of data needs to be generated to train surrogates before the optimization starts. Thus, methodologies developed for off-line data-driven EAs discussed above can also be applied in on-line data-driven EAs. In the following, we focus on the strategies for managing surrogates during the optimization.
请注意,离线数据驱动的EAs可以看作是在线数据驱动的EAs的一种特殊情况,通常,在优化开始之前,需要生成一定数量的数据来训练代理。因此,上述为离线数据驱动的EAs开发的方法也可以应用于在线数据驱动的EAs。下面,我们将重点研究优化过程中代理管理的策略。
It should be pointed out that generation of new data in on-line data-driven optimization may or may not be actively controlled by the EA. If the generation of new data cannot be controlled by the EA, the main challenge is to promptly capture the information from the new data to guide the optimization process. To the best of our knowledge, no dedicated data-driven EAs have been reported to cope with optimization problems where new data are available but cannot be actively controlled by the EA, which happens when streaming data is involved. In case the EA is able to actively control data generation, desired data can be sampled to effectively update the surrogate models and guide the optimization performance. The frequency and choice of new data samples are important for updating surrogate models. Many model management strategies have been developed, which are mostly generation-based or individual-based [9],[14]. Generation-based strategies [43] adjust the frequency of sampling new data generation by generation, while individual-based strategies choose to sample part of the individuals at each generation.
应该指出,在线数据驱动的优化所产生的“世代数据”可能是也可能不是显示由EA控制。如果新的世代数据无法由EA控制,从数据中迅速捕获信息来指导优化过程将会是很困难的。就我们所知,还没有专门的数据驱动的EAs被提出来处理优化问题,当有新数据可用但不能被EA主动控制时,就会发生流数据。如果EA能够主动控制数据生成,则可以对所需数据进行采样,从而有效地更新代理模型并指导优化性能。新数据样本的频率和选择对于更新代理模型非常重要。许多模型管理策略已经发展起来,它们大多是基于世代或基于个体的[9],[14]。基于世代的策略[43]对生成的新数据的采样频率进行调整,而基于个体的策略则选择每代抽取一部分个体进行采样。
For on-line data-driven EAs using generation-based model management strategies, the whole population in η generations is re-sampled to generate new data, then the surrogate models are updated based on the new data. The parameter η can be predefined [44], [45] or adaptively tuned according to the quality of the surrogate model [8].
对于采用基于世代模型管理策略的在线数据驱动EAs,首先对整个世代 η 的全体种群进行重新采样,生成新数据,然后根据新数据更新替代模型。参数η可以预定义为[44]、[45]或根据代理模型[8]的质量进行自适应调优。
Compared to generation-based strategies, individual-based strategies are more flexible [14], [46]. Typically, two types of sample solutions have been shown to be effective, the samples whose fitness is predicted to be promising, and those whose predicted fitness has a large degree of uncertainty according to the current surrogate.
与基于代的策略相比,基于个体的策略更加灵活。通常,有两种类型的样本解决方案被证明是有效的,一种是适应度被预测为有前途的样本,另一种是根据当前替代项预测的适应度有很大程度的不确定性的样本。
• Promising samples are located around the optimum of the surrogate model, and the accuracy of the surrogate model in the promising area is enhanced once the promis-ing solutions are sampled [8], [14].
有希望的样本位于代理模型的最优位置周围,一旦对有希望的解决方案进行采样,替代模型在有希望区域的准确性就会提高。[8]、[14]
• Uncertain samples are located in the search space where the surrogate model is likely to have a large approximation error and has not been fully explored by the EA. Thus, sampling these solutions can strengthen exploration of data-driven EAs and most effectively improve the approximation accuracy of the surrogate [7], [9], [46]. So far, different methods for estimating the degree of uncertainty in fitness prediction have been proposed [47]. Probabilistic surrogates such as Kriging models [12], [48] themselves are able to provide a confidence level for their predictions, becoming the most widely used surrogates when the adopted model management needs to use the uncertainty information. In addition, the distance from the sample solution to the existing training data has been used as an uncertainty measure in [46]. Finally, ensemble machine learning models have been proved to be promising in providing the uncertainty information, where the variance of the predictions outputted by the base learners of the ensemble can be used to estimate the degree of uncertainty in fitness prediction [49], [50].
不确定样本位于代理模型的搜索空间中可能会有一个巨大的逼近误差而EA尚未完全探索的区域。因此,取样这些解决方案可以加强勘探的数据驱动的EAs和最有效提高逼近精度的代理[7],[9],[46]。到目前为止,对适应度预测的不确定性程度的估计方法有不同的看法。概率代理,如克里格模型[12]、[48]本身能够为其预测提供一个置信水平,成为所采用的模型管理需要使用不确定性信息时最广泛使用的代理。另外,在[46]中,样本解到已有训练数据的距离被用作不确定度的度量。最后,集成机器学习模型在提供不确定性信息方面被证明是有前景的,其中集成的基础学习者输出的预测的方差可以用来估计适应度预测[49],[50]的不确定性程度。
Both promising and uncertain samples are important for on-line data-driven EAs. A number of selection criteria can be adopted to strike a balance between these two types of samples in individual-based strategies, also known as infill sampling criterion or acquisition function in Bayesian optimization [51]. Existing infill criteria include the expected improvement (ExI)[52], [53], probability of improvement (PoI) [54], and lower confidence bound (LCB) [55]. These infill criteria typically aggregate the predicted fitness value and the estimated uncer-tainty of the predicted fitness into a single-objective criterion. There are also studies that separately select these two types of samples in the individual-based strategies, for instance in [2], [50]. Most recently, a multi-objective infill criterion has been proposed [56], which considers the infill sampling as a bi-objective problem that simultaneously minimizes the predicted fitness and the estimated variance of the predicted fitness. Then, the solutions on the first and last non-dominated fronts are chosen as new infill samples. The proposed multi-objective infill criterion is empirically shown to be promising, in particular for high-dimensional optimization problems.
有前途的和不确定的样本对于在线数据驱动的EAs都是重要的。在基于个体的策略中,可以采用一些选择准则来平衡这两类样本,在贝叶斯优化[51]中又称为填充抽样准则(infill sampling criterion)或获取函数(acquisition function)。现有填充标准包括预期改进(ExI)[52]、[53]、概率改进(PoI)[54]和置信下限(LCB)[55]。这些填充标准通常将预测的适应度值和预测的适应度的估计偏差聚合为一个单目标标准。也有研究在基于个体的策略中分别选取了这两类样本,如[2],[50]。最近提出了一种多目标填充准则[56],该准则将填充采样视为一个双目标问题,同时最小化预测适应度和预测适应度的估计方差。然后,选择第一个和最后一个非主导面上的溶液作为新的填充试样。所提出的多目标填充准则的经验证明是有前途的,特别是在高维优化问题。
III. CASE STUDIES
In this section, we present five real-world data-driven optimization problems, including blast furnace optimization, trauma system design, fused magnesium furnace optimization, airfoil shape design, and design of an air intake ventilation system. Four of the five case studies involve multiple objec-tives. These five applications belong to different data-driven optimization problems in terms of data type, data amount, and availability of new data, as listed in Table I.
在本节中,我们提出五个真实世界的数据驱动优化问题,包括高炉优化,创伤系统设计,熔镁炉优化,机翼形状设计,和一个进气口通风系统的设计。5个案例研究中有4个涉及多个对象。这五个应用程序在数据类型、数据量和新数据可用性方面属于不同的数据驱动优化问题,如表I所示。
A. Off-line Small Data-Driven Blast Furnace Optimization
Blast furnaces [57] are very complex systems and running experiments with blast furnaces is costly, time-consuming, and very cumbersome due to complex reaction mechanisms. Thus, decision makers can optimize the operating conditions based only on a limited amount of experimental data.
高炉[57]是一个非常复杂的系统,由于反应机制复杂,在高炉上进行实验成本高,耗时长,而且非常繁琐。因此,决策者可以在有限的实验数据基础上优化操作条件。
In blast furnace optimization, the decision variables typically are the amount of several components to be added in the furnace, such as limestone and dolomite, quartzite, manganese, alkali and alumina additives. In total, more than 100 components can be added in the furnace, making optimization and surrogate modelling very challenging. To reduce the number of decision variables, dimension reduction techniques can be adopted by analyzing the influence of decision variables on the objectives to be optimized. The objective functions in blast furnace optimization may include the required properties of the product, and objectives related to the environmental and economic requirements as well.
在高炉优化中,决策变量通常是高炉中添加的石灰石、白云石、石英岩、锰、碱和氧化铝添加剂等几种组分的数量。总的来说,可以在炉中添加100多种成分,使优化和代理建模非常具有挑战性。通过分析决策变量对待优化目标的影响,可以采用降维技术来减少决策变量的数量。高炉优化的目标函数可能包括产品所要求的性能,以及与环境和经济要求有关的目标。
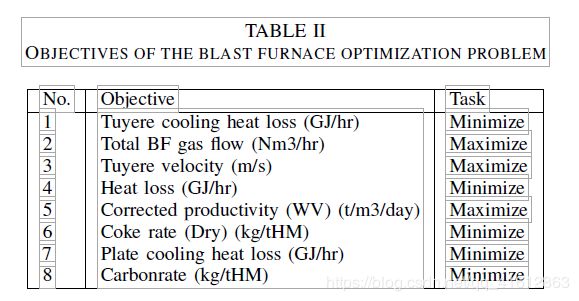
In [38], an off-line data-driven multi-objective evolutionary algorithm was reported, where 210 data points are available collected by means of real-time experiments in the furnace. The first important challenge after collecting the data is to formulate the optimization problem, i.e., to identify objective functions and decision variables. After several rounds of discussions with the expert involved, eight objectives were identified. Principle component analysis is employed to reduce the number of decision variables and eventually 12 most important decision variables were retained. The objectives and decision variables used in the optimization are presented in Tables II and III, respectively.
在[38]中,报告了一种离线数据驱动的多目标进化算法,该算法通过炉内实时实验收集了210个数据点。收集数据后的第一个重要挑战是制定优化问题,即,确定目标函数和决策变量。在同有关专家进行了几轮讨论之后,确定了八项目标。采用主成分分析法减少决策变量的数量,最终保留了12个最重要的决策变量。优化所使用的目标和决策变量分别见表II和表III。
八个目标:最小化 风口冷却热损失,最大化高炉煤气总流量,最大化风口速度,最小化热损失,最大化修正生产率,最小化焦炭率,最小化板式冷却热损失,最小化二氧化碳排放
十二个决策变量: 各种材料,氧化铝,锰,石灰石啥的,懒得翻译了。
As can be seen from Table II, several economical objectives that influence the efficiency of the furnace are also considered. They include minimizing the heat loss, maximizing the gas flow and maximizing the tuyere velocity. After identifying the objective functions and decision variables, the next challenge is to optimize these objectives to obtain optimal process conditions. As mentioned, since no analytical or simulation models are available, surrogates were built for each objective function. Kriging models [58] have been widely used in the literature [54], [59] due to their ability to provide a good approximation from a small amount of data, as well as a degree of uncertainty for the approximated values. Therefore, Kriging model was chosen as the surrogate to assist the optimization algorithm.
从表二可以看出,几个影响炉效率的经济目标也被考虑。它们包括最小化热损失,最大化气体流量和最大化风口速度。在确定了目标函数和决策变量后,下一个挑战是优化这些目标,以获得最优处理程序的条件。如上所述,由于没有可用的分析或仿真模型,因此为每个目标函数建立了代理。克里格模型[58]已被广泛应用于文献[54],[59]由于其从少量的数据中提供良好近似值的能力,以及一定程度上近似值的不确定性。因此,选择克里格模型作为代理来辅助优化算法。
The data available from the blast furnace is typically noisy and contains outliers. Therefore, pre-processing of the data was needed before building the Kriging models. In [38], a local regression smoothing technique [39] was used to smoothen the fitness landscape. In local regression smoothing, every sample in the data available is assigned with weights and a locally weighted linear regression is used to smoothen the data.
从高炉得到的数据通常是嘈杂的,并且包含异常值。因此,在建立克里格模型之前,需要对数据进行预处理。在[38]中,使用局部回归平滑技术[39]来平滑适应值曲面。在局部回归平滑中,对数据中的每一个样本进行加权,并用局部加权线性回归平滑数据。
After smoothening the data, a Kriging model was built for each objective function. The next challenge was then to select an appropriate algorithm to optimize eight objectives simultaneously. For this purpose, RVEA [40] was adopted to optimize the objective functions. RVEA was shown to be competitive on several benchmark problems compared to several EAs. RVEA differs from other many-objective evolutionary algorithms in the selection criterion and a set of adaptive reference vectors for guiding the search. The selection criterion, called angle penalized distance (APD), aims to strike a balance between convergence and diversity. The set of adaptive reference vectors makes sure that a set of evenly distributed solutions can be obtained in the objective space even for problems with different scales of objectives.
对数据进行平滑处理后,建立了各目标函数的Kriging模型。接下来的挑战是选择一个合适的算法来同时优化八个目标。为此,我们采用RVEA[40]优化目标函数。结果表明,RVEA在几个基准问题上具有较强的竞争力。与其他多目标进化算法相比,RVEA算法在选择准则和一组指导搜索的自适应参考向量方面有所不同。这种选择标准称为角度惩罚距离(APD),目的是在收敛性和多样性之间取得平衡。自适应参考向量集保证了即使对于不同目标尺度的问题,也能在目标空间中得到一组均匀分布的解。
In [38], 156 reference vectors were generated and 10000 function evaluations using the Kriging models were performed. A representative set of 100 non-dominated solutions in the objective space is presented in Fig. 5. These solutions are presented on a normalized scale to maintain the confidentiality of the data. The results clearly show a conflicting nature between the coke rate (the 6th objective in Table II) and productivity (the 5th objective). Moreover, our results show that for many solutions a conflicting nature exists between the productivity (the 5th objective) and gas velocity (the 3rd objective). These solutions were presented to experts and considered to be satisfactory and reasonable, although they remain to be verified in practice.
在[38]中,生成156个参考向量,并利用克里格模型对10000个函数进行评估。目标空间中100个非支配解的代表集如图5所示。这些解决方案分布在规范化的范围内,以保持数据的机密性。结果清楚地表明,焦炭率(表二中的第6个目标)和生产率(第五个目标)之间存在冲突。此外,我们的结果表明,对于许多解决方案,生产率(第五个目标)和气速(第三个目标)之间存在冲突。这些解决办法已提交给专家,给出令人满意和合理的方案,但仍有待在实践中加以验证。
B. Off-line Big Data-Driven Trauma System Design Optimization
The design of trauma systems can be formulated as a combinatorial multi-objective optimization problem to achieve a clinically and economically optimal configuration for trauma centers. In [6], three different clinical capability levels for different injury degrees, i.e., major trauma center (MTC), trauma unit (TU), and local emergency hospital (LEH), were assigned to 18 existing Scottish trauma centers [60]. Designing such a trauma system should be in principle based on the geospatial information, which is hard to measure accurately. However, geospatial information relevant to trauma system design can be implicitly reflected by the incidents occurred during a period of time. Thus, trauma system design based on a large number of incident records can be seen as an off-line data-driven optimization problem.
创伤系统的设计可以表述为一个组合的多目标优化问题,以实现临床和经济上创伤中心的最优配置。在[6]中,不同损伤程度的临床能力有三种不同水平,即:主要创伤中心(MTC)、创伤科(TU)和当地急诊医院(LEH)被分配到苏格兰现有的18个创伤中心[60]。设计这样的创伤系统,原则上应该基于地理空间信息,而地理空间信息很难准确测量。然而,与创伤系统设计相关的地理空间信息可以通过一段时间内发生的事件含蓄地反映出来。因此,基于大量事件记录的创伤系统设计可以看作是一个离线数据驱动的优化问题。
In evaluating a candidate configuration, all recorded incidents are re-allocated to centers matching their injuries using an allocation algorithm, which is a decision tree to provide all injured persons with matched clinical services and timely transportation to the hospital based on the degree of injuries and the location of the incidents [61]. After allocating all injured persons to an appropriate hospital by land or air, the allocation algorithm can evaluate the following four metrics.
在评估候选人的配置,所有记录的事件都将通过一种分配算法重新分配到与他们的伤害匹配的中心,这一个决策树能根据受伤的程度和事故发生的地点,为所有受伤人士提供匹配的临床服务和及时送往医院[61]。在将所有伤员通过陆地或空中分配到合适的医院后,分配算法可以对以下四个指标进行评估。
1)Total travel time: the travel time of sending all the patients from the incident locations to the allocated centers is summarized, which is a clinical metric.
总传输时间:总结所有患者从事件地点到分配中心的旅行时间,这是一个临床度量。
2)Number of MTC exceptions: some patients with very severe injuries might have to be sent to the nearest TU instead of an MTC, because the nearest MTC in the configuration is too far away. Such cases are denoted as MTC exceptions, which is a metric to assess the clinical performance of the configuration.
MTC异常的数量:一些严重受伤的病人可能不得不被送到最近的TU而不是MTC,因为配置中最近的MTC太远了。这样的情况被表示为MTC异常,这是一个指标,以评估临床性能的配置。
3)Number of helicopter transfers: some patients must be sent by air due to a large distance from the incident location to the hospital to be sent to. The number of helicopter transfers is an economical metric.
直升机转送次数:有些病人因距离事发地点较远,必须空运。直升机转移的数量是一个经济指标。
4)MTC volume: the number of patients sent to each MTC in the configuration shows its obtained clinical experience.
MTC量:配置中发送到每个MTC的患者数量显示其获得的临床经验。
In [62], the first two metrics (total travel time and number of MTC exceptions) were set as objectives (f1 and f2) and the other two (number of helicopter transfers and MTC volume) as constraints. Moreover, the distance between any two TUs in the configuration is constrained, which is not based on the metrics of the simulation. Given the formulation, the trauma system design problem was solved by NSGA-II [63] in [62], where 40,000 incidents (ambulance service patients with their locations and injuries) in one year served as the data for optimization.
在[62]中,前两个指标(总旅行时间和MTC例外数量)被设定为目标(f1和f2),另外两个指标(直升机传输数量和MTC量)被设定为约束条件。此外,配置中任意两个节点之间的距离也受到了约束,而不以仿真的度量为基础。考虑到这一公式,NSGA-II[63]在[62]中解决了创伤系统设计问题,其中以一年40000起事故(救护车服务患者及其位置和受伤情况)为数据进行优化。
Note that evaluating each configuration needs to calculate the objectives and constraints using all data, which makes the function evaluations expensive. For example, it took over 24 hours for NSGA-II to obtain satisfactory results [62]. To reduce such high computational costs, a multi-fidelity surrogate management strategy was proposed to be embedded in NSGA-II in [6].
请注意,评估每个配置需要使用所有数据计算目标和约束,这使得功能评估代价高昂。例如,NSGA-II需要超过24小时才能得到满意的结果[62]。为了降低如此高的计算代价,我们提出了一种多保真度代理管理策略,嵌入到[6]的NSGA-II中。
As the incidents are distributed with a high degree of spatial correlation [64], the data can be approximated by a number of data clusters, which is usually much smaller than the number of data. In this case, it is not necessary to use all data records for function evaluations, and fitness calculations based on the clustered data can be seen as surrogate models approximat-ing the function evaluations [6]. It is conceivable that the approximation error decreases as the number of clusters K increases, but the computational cost increases as well. The multi-fidelity surrogate management strategy [6] tuned the number of clusters as the optimization proceeded according to the allowed root mean square error (RMSE) of the surrogate model on f1. It is well known that the selection in NSGA-II is based on the non-dominated sorting [65], [66], where the population combining the parent and offspring solutions is sorted into several non-dominated fronts and the better half of the individuals in the combined population is selected as the parent population for the next generation. Thus, the allowed maximum approximation error should not lead to the consequence that solutions in the first front are ranked after the last selected front due to approximation errors. Therefore, the allowed maximum error ER∗ was defined as follows:
where F1 is the solution set of the first front and Fl is the solution set of the last selected front. As the evolutionary search of NSGA-II proceeds, the population gets concentrated and moves towards the true Pareto front (PF), and the allowed error ER∗ decreases as the number of clusters increases.
由于事件的分布具有高度的空间相关性[64],数据可以近似为若干数据簇,这些数据簇通常比数据的数量小得多。在这种情况下,没有必要使用所有数据记录进行函数评估,基于聚类数据的适应度计算可以看作是近似函数评估[6]的替代模型。可以想象,近似误差会随着聚类K的增加而减小,但计算代价也会增加。多保真度代理管理策略[6]根据代理模型在f1上允许的均方根误差(RMSE)调整集群数量。众所周知,NSGA-II的选择是基于non-dominated排序[65],[66],父代和子代所有种群相结合并分成几个非支配目标域,更好的一个目标域的种群被选中作为下一代的父代种群。因此,允许的最大逼近误差不应该导致第一个目标域的解由于逼近误差排在最后一个目标域上。因此,允许最大误差ER定义如下
其中F1为第一个目标域的解集,Fl为最后选择的目标域的解集。随着NSGA-II的进化搜索的进行,种群变得集中并向真正的非劣最优目标域 (PF)移动,允许的错误ER随着集群数量的增加而减少。
Fitness evaluations using the entire data were replaced by surrogate models based on K-clusters of data in NSGA-II. In each generation, the non-dominated solutions were evaluated by the whole data simulation to estimate the error ER of the surrogate model based on K-clustered data. Thus, the relationship between the surrogate error and K was estimated according to the following regression model (K, ER):
在NSGA-II中,使用整个数据的适应度评估被基于k -聚类数据的替代模型代替。在每一代中,通过全数据模拟对非支配解进行评估,以估计基于k聚类数据的替代模型的误差。因此,根据以下回归模型(K, ER)估计替代误差与K的关系
Given the regression parameters β1 and β2 and the allowed error ER∗, the adjusted number of clusters K∗ can be calculated from Equation (2) as shown in Fig. 6.
给定回归参数β1 ,β2和允许的误差ER∗,可以从公式(2)计算出经过调整的集群数量K∗,如图6所示。
By embedding the multi-fidelity surrogate management strategy in NSGA-II [6], we describe the algorithm (called SA-NSGA-II) as follows.
通过在NSGA-II[6]中嵌入多保真度代理项管理策略,我们如下描述算法(称为SA-NSGA-II)。
1) Initialization
• Set K to be 18 (the number of hospitals in the system). Cluster the data into K categories.
• Generate a random initial population and evaluate the population using the surrogate based on K-clustered data.
1)初始化
•设置K为18(系统中医院的数量)。将数据聚类到K个类别中。
•生成一个随机初始种群,并使用基于k聚类数据的代理来评估种群。
2)Reproduction: Apply 3-point crossover (probability of 1) and point mutation (probability of 0.2) to the parent population for the offspring population, evaluate the offspring population using the surrogate based on K-clustered data.
2)繁殖:对子代种群的亲本种群进行3点交叉(概率为1)和点突变(概率为0.2),利用基于k聚类数据的代理对子代种群进行评估。
3) Selection: Combine the parent and offspring popu-lations, select the parent population based on non-dominated sorting and crowding distance.
选择:结合亲本和子代种群,根据非主导排序和拥挤距离选择亲本种群。
4) Fidelity adjustment
• Detect the improvement of the non-dominated solution set. Apply the following steps to adjust K if there is no improvement; otherwise, keep K unchanged.
• Calculate the fitness of the non-dominated solutions using the whole data. Estimate the approximation error ER of the surrogate based on K-clustered data, and record the estimated pair (K, ER).
• Estimate the relationship between ER and K by the regression model in Equation (2) from those estimated pairs (K, ER).
• Calculate the allowed error ER∗ as Equation (1). If ER∗ is smaller than half of ER, set ER∗ = ER/2.
• Estimate the new K∗ by ER∗ based on the obtained regression model if there are enough historical pairs to obtain the regression model, otherwise K∗ = 2K. If K∗ exceeds the limit Kmax, set K∗ = Kmax.
• Re-cluster the data into K∗ categories.
• Evaluate the parent population using the surrogate based on K∗-clustered data.
4)保真度调整
•检测非占主导的解集合的改善情况,如无改善,按以下步骤调整K;否则,保持K不变。
•使用整个数据计算非主导解决方案的适合度。基于K聚类数据估计代理的近似误差ER,并记录估计的对(K, ER)。
•根据这些估计对(K, ER),利用方程(2)中的回归模型估计ER与K的关系。
•用公式(1)计算允许的错误ER∗如果ER∗小于ER的一半,设ER∗= ER/2。
•根据获得的回归模型估计新的K∗by ER∗如果有足够的历史对来获得回归模型,否则K∗= 2K。如果K∗超过Kmax的限制,设置K∗= Kmax。
•将数据重新聚类到K个∗类别。
•基于K个∗-clustered数据使用代理来评估父种群。
5)Stopping criterion: If the stopping criterion is satisfied, output the non-dominated solutions, otherwise go to step 2).
停止条件:如果满足停止条件,输出非支配解,否则进入步骤2)。
SA-NSGA-II is an off-line data-driven EA as no new data can be actively generated during the optimization. Experimental results have shown that SA-NSGA-II can save up to 90 percent of the computation time of NSGA-II [6]. Although the lack of on-line data limits the performance of off-line data-driven EAs, making full use of the off-line data can effectively benefit the optimization process as well. Therefore, handling the off-line data affects the optimization process. We compare the performance of NSGA-II run for 100 generations with its variants using different data handling strategies on the trauma system design problem. The three compared strategies are described below
SA-NSGA-II是一个脱机的数据驱动EA,因为在优化过程中不会主动生成新数据。实验结果表明,SA-NSGA-II可以节省高达90%的NSGA-II[6]的计算时间。虽然缺少在线数据限制了离线数据驱动的EAs的性能,但是充分利用离线数据也可以有效地促进优化过程。因此,离线数据的处理影响了优化过程。我们比较了NSGA-II在创伤系统设计问题上使用不同数据处理策略运行100代的性能及其变体。下面介绍三种策略
• Random sampling: Before running NSGA-II, K data points are randomly selected from the whole data for function evaluations.
• Clustering: Before running NSGA-II, the whole data is divided into K clusters, which is fixed during the optimization.
• Adaptive clustering: SA-NSGA-II is used for the comparison, where the data is adaptively clustered for function evaluations in optimization.
•随机抽样:在运行NSGA-II之前,从整个数据中随机选取K个数据点进行函数评估。
•聚类:在运行NSGA-II之前,将整个数据分成K个聚类,在优化过程中,K是固定的。
•自适应聚类:SA-NSGA-II用于比较,其中数据自适应聚类用于优化中的功能评估。
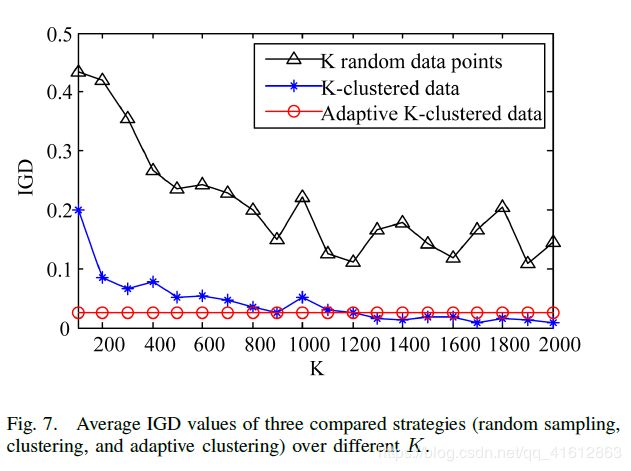
As Kmax in SA-NSGA-II is set to 2000 [6], we assume that K ranges from 100 to 2000. All the compared algorithms run independently for 20 times. IGD [67], the average distance from a reference PF set to the obtained solution set, is used to assess the performance of compared algorithms. The same settings as in [6] are used, where the reference PF set is obtained from the non-dominated set of 5 runs of NSGA-II based on the whole data. The average IGD values of three compared strategies (random sampling, clustering, and adaptive clustering) over various K values are shown in Fig. 7.
由于SA-NSGA-II中的Kmax被设为2000[6],我们假设K的取值范围为100 - 2000。所有比较算法独立运行20次。IGD[67]是指参考PF集到所得到解集的平均距离,用于评估比较算法的性能。使用与[6]中相同的设置,其中参考PF集是从基于整个数据运行5次NSGA-II的非主导集获得的。三种比较策略(随机抽样、聚类和自适应聚类)对不同K值的IGD平均值如图7所示。
From Fig. 7, we can see that for the two variants using random sampling and clustering, the IGD values decrease with an increasing K, because the more data points are used in function evaluations, the more accurate the fitness calculations are. In fact, randomly sampling K data points for the function evaluations fails to extract the data pattern, while a relatively small number of representative data points are still able to describe the main feature of the whole data. Therefore, IGD values resulting from the random sampling strategy are larger (worse) than those from the clustering strategy for various sizes of K. Although a large K leads to better performance, the computational cost becomes higher. From the results in Fig. 7, we can see that the adaptive clustering strategy uses various Ks (up to 2000) during the optimization results in a similar IGD value obtained by using 2000-clustered data, although the former strategy requires much less computational resources than the latter.
从图7可以看出,对于随机抽样和聚类的两个变量,IGD值随着K的增加而减小,这是因为函数评估中使用的数据点越多,适应度计算越准确。事实上,随机抽取K个数据点进行函数评估并不能提取出数据模式,而相对较少的代表性数据点仍然能够描述整个数据的主要特征。因此,对于不同大小的K,随机抽样策略产生的IGD值比聚类策略产生的IGD值更大(更差)。虽然K值越大,性能越好,但计算代价越高。从图7的结果可以看出,自适应聚类策略在使用2000聚类数据的优化结果中使用了不同的Ks(最多2000),尽管前者需要的计算资源比后者少得多。
From the above experimental results, we can conclude that a properly designed model management strategy can effectively enhance the computational efficiency of the optimization with-out a serious degradation of the optimization performance.
从以上实验结果可以看出,适当设计的模型管理策略可以在不严重降低优化性能的前提下,有效提高优化计算效率。
C. Off-line Small Data-Driven Optimization of Fused Magnesium Furnaces
The performance optimization of fused magnesium furnaces aims at increasing the productivity and enhancing the quality of magnesia products while reducing the electricity consumption in terms of optimized set points of electricity consumption for a ton of magnesia (ECT) [68]. Before a production batch, the ECT of every furnace is set by an experienced operator according to the properties of raw materials and the condition of each furnace. Optimizing such a problem should be based on the relationship between ECT set points and each performance index. However, it is very hard, if not impossible, to build analytical functions because of complex physical and chemical processes involved, intermittent material supplies, and sensor failures. As a result, one has to turn to limited and noisy historical production data for optimizing the performance of fused magnesium furnaces, making it an off-line data-driven optimization problem.
熔镁炉的性能优化旨在提高生产率和提高镁砂产品的质量,同时减少一吨镁砂(ECT)的电力消耗的优化设定值[68]。在批量生产前,每个炉的ECT由经验丰富的操作人员根据原料的特性和每个炉的情况进行设置。优化该问题应基于ECT设定值与各性能指标之间的关系。然而,由于涉及复杂的物理和化学过程、断断续续的材料供应和传感器故障,要建立分析函数即使不是不可能,也是非常困难的。因此,为了优化熔镁炉的性能,人们不得不求助于有限且嘈杂的历史生产数据,使其成为一个离线的数据驱动的优化问题。
Only a small number of noisy data is available because one production batch lasts 10 hours. There are 60 groups of ECT set points and performance indicators for five furnaces, which are all the furnaces connected to one transformer. Therefore, the decision variables are the ECT set points of five furnaces, and the objectives are the average high-quality rate, total output and electricity consumption of five furnaces.
因为一个生产批次持续10小时,所以只有少量的噪声数据可用。5个炉有60组ECT设定值和性能指标,都是连接到一个变压器上的炉。因此,决策变量为五炉的ECT设定值,目标为五炉的平均优良率、总产出和电耗。
Given a small amount of noisy data, it is hard to construct accurate surrogates. In the GP-assisted NSGA-II [42], termed NSGA-II GP, two surrogates are built for model management, as shown is Fig. 8. One is a low-order polynomial regression model constructed using the off-line data. This low-order model approximates the unknown real objective function to generate synthetic data for model management, playing the role of the real objective function. The reason for adopting a low-order polynomial model is that it is less vulnerable to over-fitting. The other surrogate is a Kriging model, which is built based on both off-line data and synthetic data. Here, the most promising candidate solutions predicted by the Kriging model are further evaluated using the low-order polynomial model, and the synthetic data generated by the polynomial model are used to update the Kriging model for the next generation. In optimization, expected improvement [53] is adopted to identify the most promising candidate solutions, and k-means clustering is applied in the decision space to choose sampling points, while fuzzy c-means clustering [69] is introduced to limit the number of data for training the Kriging model.
给定少量的噪声数据,很难构建准确的替代。GP辅助的NSGA-II[42],称为NSGA-II GP,构建了两个代理进行模型管理,如图8所示。一个是利用离线数据构建的低阶多项式回归模型。该低阶模型近似未知的真实目标函数,生成用于模型管理的综合数据,起到真实目标函数的作用。采用低阶多项式模型的原因是它不易发生过拟合。另一种替代方法是基于离线数据和合成数据建立的Kriging模型。在此,利用低阶多项式模型对克立格模型预测的最有希望的候选解进行进一步评估,并利用多项式模型生成的合成数据对克立格模型进行下一代的更新。优化中采用期望改进[53]来识别最有希望的候选解,在决策空间中采用k-means聚类来选择采样点,引入模糊c-means聚类[69]来限制训练克里格模型的数据数量。
The biggest challenge in the off-line data-driven perfor-mance optimization of magnesium furnaces is how to verify the effectiveness of a proposed algorithm due to the lack of real objective functions. To address this issue, the performance of the proposed method was first verified on benchmark problems. During optimization, it is assumed that the real objective function is not available except for a certain amount of data generated before optimization. The resulting optimal solutions are then verified using the real objective functions to assess the effectiveness of the proposed algorithm. Once the algorithm is demonstrated to be effective, it can then be applied to real-world problems. This strategy is illustrated in Fig. 9. To simulate the small amount of noisy data in the furnace performance optimization problem, Latin hypercube sampling (LHS) [70] is first used to generate off-line data using the objective functions of the benchmark problems, to which noise is then added. The noise is generated according to the following equation:
where rand is a random number within [-0.1,0.1], and fjmin and fjmax are the minimum and maximum of real function values of the off-line data in the j-th objective, respectively. In numerical simulations on nine benchmark problems, NSGA-II GP was compared with the original NSGA-II and a popular surrogate-assisted multi-objective EA, ParEGO [71]. The re-sults on the benchmark problems consistently showed that the performance of NSGA-II GP is the best.
在镁炉离线数据驱动性能优化中,由于缺乏真实的目标函数,如何验证算法的有效性是最大的挑战。为了解决这个问题,首先在基准问题上验证了所提方法的性能。在优化过程中,假设只有优化前生成一定数量的数据,才能得到真实的目标函数。然后用真实目标函数验证所得到的最优解,以评估所提算法的有效性。一旦该算法被证明是有效的,它就可以应用于实际问题。该策略如图9所示。为了模拟高炉性能优化问题中少量的噪声数据,首先使用拉丁超立方体采样(LHS)[70]利用基准问题的目标函数生成离线数据,然后添加噪声。噪声由下式产生
其中rand为[-0.1,0.1]内的随机数,fjmin和fjmax分别为第j个目标离线数据实函数值的最小值和最大值。在9个基准问题的数值模拟中,NSGA-II GP与原始NSGA-II和流行的代理辅助多目标EA ParEGO进行了比较[71]。对基准问题的分析结果一致表明,NSGA-II GP的性能最好。
In optimizing the furnace performance, first and second order polynomial models are considered to fit the collected production data, and the fitting results of one furnace are plotted in Fig. 10. After the formulation of the furnace performance optimization problem, NSGA-II GP is applied and the optimization results are plotted in Fig. 11, which shows that NSGA-II GP has found better ECT set points compared to the off-line data. From the results on benchmark problems and furnaces performance optimization problem, we can conclude that different accuracy surrogates are very helpful to off-line small data-driven optimization.
在优化加热炉性能时,采用一阶和二阶多项式模型拟合收集的生产数据,其中一个加热炉的拟合结果如图10所示。在制定炉况性能优化问题后,应用NSGA-II GP,优化结果如图11所示,可以看出NSGA-II GP比离线数据找到了更好的ECT设定值。从基准问题和炉窑性能优化问题的结果可以看出,不同的精度替代对离线小数据驱动优化有很大的帮助。
D. On-line Small Data-Driven Optimization of Airfoil Design
Airfoil design is one important component in aerodynamic applications, which changes the airfoil geometry to achieve the minimum drag over lift ratio. However, the evaluation of airfoil geometry is based on time-consuming CFD simulations, therefore only a small number of expensive evaluations is allowed during the design process, resulting in an on-line data-driven optimization problem.
翼型设计是气动应用中的一个重要组成部分,它通过改变翼型的几何形状来实现最小的升阻比。然而,翼型几何的评估是基于耗时的CFD模拟,因此在设计过程中只允许进行少量昂贵的评估,导致一个在线数据驱动的优化问题。
The geometry of an airfoil is represented by a B-spline curve consisting of 14 control points [50]. Therefore, the decision variables are the positions of those 14 control points. The objective is to minimize the average drag over lift ratio in two design conditions, where the drag and lift are measured based on the results from CFD simulations.
机翼的几何图形由14个控制点[50]组成的B-spline曲线表示。因此,决策变量为14个控制点的位置。其目标是最小化两种设计条件下的平均阻力比,其中阻力和升力是根据CFD模拟结果测量的。
In this specific design of RAE2822 airfoil, there are 70 off-line data points describing the relationship between different geometries and their evaluated objective value. In addition, 84 new samples are allowed to be generated during the optimization. The recently proposed on-line data-driven EA, committee-based active learning based surrogate-assisted particle swarm optimization (CAL-SAPSO) was employed to solve the airfoil design problem in [50].
在本次RAE2822翼型的具体设计中,有70个离线数据点描述了不同几何形状与其评估的客观值之间的关系。优化过程中允许生成84个新样本。采用最近提出的在线数据驱动EA,基于代理辅助粒子群优化 (calo - sapso)来解决[50]的翼型设计问题。
CAL-SAPSO uses two surrogate ensembles composed of a polynomial regression model, an RBFN, and a Kriging model [72] to approximate the expensive objective. One ensemble serves as a global model built from the whole data, while the other is meant to be a local model built from the data belonging to the best 10% objective values found so far. CAL-SAPSO begins with search on the global model, and then switches to the local model when no improvement can be achieved. The found best solutions are always evaluated using the real objective function and both surrogate models are then updated. The two models are used and updated in turn until the allowed maximum number of fitness evaluations is exhausted.
calo - sapso使用了由多项式回归模型、RBFN和Kriging模型组成的两个替代集合[72]来逼近昂贵的目标。一个集合是根据整个数据建立的全局模型,而另一个集合是根据迄今为止发现的最好的10%客观值的数据建立的局部模型。CAL-SAPSO首先搜索全局模型,当没有改进时切换到局部模型。找到最佳解决方案后使用真实的目标函数进行评估,然后更新两个替代模型。轮流使用和更新这两个模型,直到用尽所允许的最大适应度评估数。
The model management strategy in CAL-SAPSO is individual-based, as shown in Fig. 12. Three types of candidate solutions are to be re-evaluated using the real objective function to update the global and local models. A canonical PSO algorithm [73] using a population size of 100 is run for a max-imum of 100 iterations. As the model management strategy of CAL-SAPSO is based on query by committee (QBC) [74], the uncertainty is measured by the largest disagreement among the ensemble members. For the global model, the most uncertain solution xu is searched for at first using PSO based on the following objective function:
CAL-SAPSO的模型管理策略是基于个体的,如图12所示。利用真实目标函数对三种候选解进行重新评估,以更新全局和局部模型。一个使用种群大小为100的典型粒子群算法[73]的最大迭代次数为100次。由于CAL-SAPSO的模型管理策略是基于query by committee(,QBC)[74],因此不确定性是通过集合成员之间的最大分歧来度量的。对于全局模型,首先使用基于以下目标函数的粒子群算法搜索最不确定解xu
where fˆi and fˆj (1 ≤ i, j ≤ 3) is the i-th and j-th models in the surrogate ensemble. After xu is evaluated using CFD simulations and added to on-line data, the global surrogate ensemble is updated. Then, PSO is used to search for the optimum xf of the global model as:
式子(4)中,fi和fj (1 ≤ i, j ≤ 3)是代理集合中的第i个和第j个模型。在使用CFD模拟对xu进行评估并将其添加到在线数据中后,对全局代理集成进行更新。然后利用粒子群算法搜索全局模型的最优xf
where fˆens(x) is the global surrogate ensemble. After xf is evaluated using CFD simulations and added to on-line data, the global surrogate ensemble is updated again. If xf is not the better than the best solution found so far, CAL-SAPSO switches to the local surrogate ensemble to continue the search. For the local model, only the optimum xls of the local model is chosen to be re-evaluated using the real objective function, which is searched using PSO based on
式子(5)中,f^ ens(x)是全局代理集合。在使用CFD模拟对xf进行评估并将其添加到在线数据后,将再次更新全局代理集。如果xf不是迄今为止找到的最好的解决方案,那么CAL-SAPSO切换到局部代理集合继续搜索。对于局部模型,仅选取局部模型的最优xls,利用基于粒子群算法的真实目标函数对其进行重新求解
where fˆlens(x) is the local surrogate ensemble. After xls is evaluated with the CFD simulations and added to on-line data, the local surrogate ensemble is updated. If xls is not better than the best geometry found so far, CAL-SAPSO switches to the global surrogate ensemble to continue the search.
式子(6)中fˆlens(x)为局部代理集。在使用CFD模拟对xls进行评估并将其添加到在线数据之后,将更新局部代理集。如果xls没有比目前找到的最好的更好,那么CAL-SAPSO切换到全局代理集来继续搜索。
CAL-SAPSO was run on the airfoil design problem for 20 times. The best geometry obtained is shown in Fig. 13, where the objective values are normalized with the objective value of the baseline design. We can see that the solution found by CAL-SAPSO achieved a 35% improvement of the drag over lift ratio over the baseline design using 70 off-line CFD simulations before optimization and 84 ones during the optimization (a total of 154 CFD simulations), which is promising in the application of aerodynamic engineering.
CAL-SAPSO在机翼设计问题上运行了20次。得到的最佳几何图形如图13所示,其中目标值与baseline设计的目标值进行了归一化。我们可以看到解决方案发现CAL-SAPSO相对于baseline取得了35%升阻比提高。在优化过程中,使用70离线CFD模拟优化和84个离线CFD模拟优化(总共154 CFD模拟),这一切说明了在空气动力工程应用中的效果。
E. On-line Small Data-Driven Optimization of An Air Intake Ventilation System
An air intake ventilation system of an agricultural tractor was considered in [2] for maintaining a uniform temperature inside the cabin and defrost the windscreen. The particular component of interest consist of four outlets and a three-dimensional CATIA model of the component is shown in Fig. 14. To maintain a uniform temperature distribution, the flow rates from all the outlets should be the same. However, these outlets had different diameters and maintaining the same flow rate from all the outlets is not trivial. In addition, the pressure loss should be minimized to increase the energy efficiency of the system. Thus, the optimization problem involves computationally expensive CFD simulations. Before starting the solution process, an initial design used in the ventilation system was provided by the decision maker and a CFD simulation of this initial design is shown in Fig. 15.
在[2]中考虑了一种农业拖拉机进气通风系统,该系统可以保持机舱内温度均匀,并对挡风玻璃进行除霜。感兴趣的特定组件由四个出口组成,该组件的三维CATIA模型如图14所示。为了保持均匀的温度分布,所有出口的流量应该是相同的。然而,这些出口有不同的直径和保持相同的流量从所有出口是很难的。此外,应尽量减小压力损失,以提高系统的能源效率。因此,优化问题涉及计算昂贵的CFD模拟。在开始求解过程之前,决策者提供通风系统的初始设计,该初始设计的CFD模拟如图15所示。
From Fig. 14, we can see that outlet 4 has the smallest diameter compared to the other outlets. Therefore, it is very difficult to make the flow rate from outlet 4 to be equal to those from other outlets. To address this issue, special attention was paid to the flow rate from this outlet. Based on several discussions with an aerodynamic expert, a three-objective optimization problem was finally formulated as follows:
从图14可以看出,出口4的直径相对于其他出口最小。因此,很难使4出口的流量与其他出口的流量相等。为了解决这个问题,应该更加关注这个出口的流量。在与气动专家多次讨论的基础上,最后给出了一个三目标优化问题
f1 : Minimize variance between flow rates at outlets 1 to 3
: Minimize var(Q1,3)
f2 : Minimize pressure loss of the air intake
: Minimize Pinlet − Poutlet
f3 : Minimize the difference between the flow rate at outlet 4
f1:尽量减少1至3出口的流量差异
:最小化var (Q1, 3)
f2:尽量减少进气口的压力损失
:减少小Pinlet - Poutlet
f3:使出口4的流量差最小
and the average of the flow rates at outlets 1 to 3 : Minimize avg(Q1,3) − Q4,
出口1到出口3的平均流量相加:使平均流量(Q1,3)−Q4最小化,
where Qk represents the flow rate from the kth outlet, avg(Q1,3) the average flow rate values from outlets 1-3 and Pinlet, and Poutlet are the pressure values at the inlet and the outlet, respectively. Note that Poutlet is the same among all outlets and equal to the atmospheric pressure.
其中Qk为第k个出口的流量,avg(Q1,3)为出口1-3的平均流量值,Pinlet,Poutlet分别为进口和出口的压力值。注意,所有出口的Poutlet是相同的,等于大气压力。
The third objective makes sure that the flow rate from outlet 4, which has the smallest diameter, can have the same flow rate to the average of flow rates from other outlets. As mentioned, the diameters play a vital role in maintaining a uniform flow rate, therefore the scaling factors of the initial design diameters are used as the decision variables:
第三个目标是确保最小直径的出口4的流量与其他出口的平均流量相同。如前所述,直径对于保持均匀的流量起着至关重要的作用,因此我们将初始设计直径的比例因子作为决策变量:
where Di is the diameter of the ith outlet and Di^initial is the diameter of the ith outlet in the initial design. The lower (xi^lb) and the upper (xi^ub) bounds of the decision variables are as follows:
(7)式中Di为第i个出口的直径,Di^initial为初始设计第i个出口的直径。决策变量的下界(xi^lb)和上界(xi^ub)如下:
为了优化,使用了kriging辅助进化算法来求解至少有三个目标的优化问题,称为K-RVEA[12]。算法使用来自底层RVEA[40]的元素来有效地管理代理。在K-RVEA中选择的样本是为了在收敛性和多样性之间取得平衡。KRVEA的另一个特点是限制了训练样本的大小以减少计算时间。算法流程图如图17所示,其中存档A1用于存储训练样本,存档A2用于存储所有评估样本。
In the algorithm, a number of initial candidate designs are generated using Latin hypercube sampling, which are evaluated with CFD simulations. The evaluated candidate solutions are added to the archives A1 and A2. Kriging models are built for each objective function by using the samples in A1. After running RVEA with the Kriging models for a prefixed number of iterations, samples are selected to update the Kriging models. These samples are selected based on the needs of convergence and diversity which are identified using the reference vectors. Every time the surrogates are updated, the change in the number of empty reference vectors compared to that in the previous update is measured. If the change is less than a predefined parameter, convergence is prioritized. Otherwise, diversity is used as the criterion in selecting candidate solutions to be evaluated using CFD simulations. A fixed number of evenly distributed samples is selected based either on their angle penalized distance, which is the selection criterion in RVEA, or on uncertainty values from the Kriging models.
在该算法中,使用拉丁超立方体采样生成大量的初始候选设计,并通过CFD模拟对其进行评估。已评估的候选解决方案被添加到归档文件A1和A2中。利用A1中的样本对每个目标函数建立克里格模型。在与克里格模型运行预定迭代次数的RVEA后,选择样本更新克里格模型。这些样本的选择是基于收敛和多样性的需要,并使用参考向量识别。每次更新代理时,测量与前一次更新相比的空参考向量数量的变化。如果变化小于预定义的参数,则优先考虑收敛。此外,多样性被用来作为选择候选解决方案的标准,以进行CFD模拟评估。根据RVEA中的角度惩罚距离(angle penalized distance)或克里格模型的不确定性值(uncertainty values),选择固定数量的均匀分布的样本。
We used a maximum of 200 expensive function evaluations (CFD simulations) in K-RVEA. Forty non-dominated solutions were generated, which are shown in Fig. 18 in the objective space. The values of the objective functions are normalized to maintain the data confidentiality. These solutions were presented to an aerodynamic expert and a final solution was selected based on his preferences. The final solution and the solution corresponding to the initial design are also shown in Fig. 18. The final selected design has an equal pressure loss (the second objective) but significant improvements in the first and the third objectives (related to minimization of differences between the flow rates) compared to the initial design. A good balance in flow rates means more can be passed into the cabin without any extra consumption of energy.
我们在K-RVEA中使用了最多200个昂贵的功能评估(CFD模拟)。生成40个非支配解,在目标空间如图18所示。对目标函数的值进行归一化,以保持数据的机密性。这些解决方案被提交给一个空气动力学专家,并根据他的喜好选择最终的解决方案。最终解和初始设计对应的解如图18所示。最终选择的设计具有相同的压力损失(第二个目标),但与初始设计相比,在第一个和第三个目标(与流量差异最小化有关)有显著的改进。一个良好的流量平衡意味着更多的能量可以进入舱内而不消耗任何额外的能量。
IV. CHALLENGES AND PROMISES
A. On-line Data-Driven Optimization
In on-line data-driven optimization, the main goals are to enhance the accuracy of the surrogate models and balance the convergence and diversity. Thus, model management is critical in on-line data-driven EAs. In an ideal scenario, any EA can be used in on-line data-driven optimization. However, in reality, the EA and the surrogates should be integrated seamlessly to ensure the success of the surrogate-assisted optimization algorithm. In the following, we highlight a few major challenges in on-line data-driven optimization.
在在线数据驱动优化中,主要目标是提高替代模型的准确性和平衡收敛性和多样性。因此,在联机数据驱动的EAs中,模型管理是至关重要的。在理想的场景中,任何EA都可以用于在线数据驱动优化。然而,在现实中,EA和代理应该无缝集成,以确保代理辅助优化算法的成功。下面,我们将重点介绍在线数据驱动优化中的几个主要挑战。
Selection of surrogate models: When developing an on-line data-driven EA, the first challenge is to select an appropriate surrogate model. Several surrogate models, e.g., Kriging, ANN, RBFN, and support vector regression can be used and there is very little theoretical guidance in the literature for choosing the surrogate model. In many cases, a surrogate model is selected based on the experience of the user (e.g., an engineer). For instance, RBFN was used in [77] to solve an optimization problem of coastal aquifer management because of its popularity for groundwater applications. Generally speaking, however, stochastic models such as Kriging models may be preferred if an infill criterion is to be used for model management. As discussed in [49], the main limitation of Krig-ing models is their possibly large computational complexity when a large number of training samples is involved. In this case, ensembles are good alternatives to Kriging models due to their scalable computational complexity.
代理模型的选择:在开发在线数据驱动的EA时,第一个挑战是选择合适的代理模型。可以使用几种替代模型,如Kriging、ANN、RBFN、支持向量回归等,文献中对于选择替代模型的理论指导很少。在许多情况下,代理模型是根据用户的经验选择的(例如,工程师)。例如,由于RBFN在地下水应用方面的普及,[77]将其用于解决沿海含水层管理的优化问题。然而,一般来说,如果模型管理采用填充标准,则采用克里格模型等随机模型。正如[49]中所讨论的,Krig-ing模型的主要限制是当涉及大量的训练样本时,计算复杂度可能很大。在这种情况下,由于可伸缩的计算复杂度,集成是克里格模型的好替代品。
Using surrogate models: Once surrogate models are selected, the next question is how to use them in the EA. For instance, approximating objective functions [10], classifying samples according to their fitness [78], predicting ranks [79], or hypervolume [80] or approximating a scalarizing function by converting a multi-objective optimization problem to a single-objective problem [71], [81] and approximating the PF [82] are possible ways of using a surrogate model.
使用代理模式:代理模型被选中后,接下来的问题是如何在EA中使用它们。例如,近似目标函数[10],根据他们的适用性(fitness)分类样本[78],预测排名[79],或超体积[80]或逼近标量函数将多目标优化问题转化为一个简略的问题[71],[81],逼近PF[82]也许是使用代理模型的方法。
Selection of training data: How to select the training data is another challenge. In on-line data-driven optimization, surrogates need to be continuously updated to enhance their accuracy and to improve the exploration of the EA as well. Samples for training should be selected in such a way that both convergence and diversity are taken into account. Most on-line data-driven EAs start with generating a number of candidate solutions using a design of experiment technique, e.g., LHS [70]. Afterwards, a model management strategy, including popular infill criteria such as expected improvement [83] and many other generationor individual-based model management strategies [9] can be used for selecting candidate solutions to be re-evaluated using the real objective functions and then re-train or update the surrogates. All sampling techniques and model management strategies have advantages and limitations and could be tailored to a particular class of problems as well as the EA used.
训练数据的选择:如何选择训练数据是另一个挑战。在在线数据驱动优化中,代理需要不断更新,以提高其准确性,并改善EA的探索。训练样本的选择应兼顾收敛性和多样性。大多数在线数据驱动的EAs都是从使用实验技术的设计生成许多候选解决方案开始的,例如LHS[70]。然后,一个模型管理策略,包括流行的填充标准,如预期改进[83]和许多其他代或基于个体的模型管理策略[9],可用于选择候选解决方案,以重新评估使用真实的目标函数,然后再训练或更新代理。所有的抽样技术和模型管理策略都有优点和局限性,并且可以像EA所使用的那样针对特定的问题类型进行调整。
Size of training data: Another important challenge, which is usually overlooked in many on-line optimization algorithms is the size of the training data. For example, using a large num-ber of samples may dramatically increase the computational complexity, in particular when the Kriging model is employed as the surrogate. Therefore, one should pay attention to using an appropriate size of data for training in on-line data-driven optimization.
训练数据的大小:另一个重要的挑战是训练数据的大小,这在许多在线优化算法中经常被忽视。例如,使用大量的样本可能会极大地增加计算复杂度,特别是当使用克里格模型作为替代时。因此,在在线数据驱动优化训练中应注意使用合适的数据量。
Selection of EA: As mentioned, a model management strategy needs to be employed to select candidate solutions for evaluation using the real objective functions and for training the surrogates. In many on-line optimization algorithms in the literature, not much attention has been paid towards the selection of EAs. This can be attributed to the assumption that a good approximation or near-optimal solution can be obtained by any EA. However, in reality, different EAs have different advantages and limitations and they should be used based on the properties of the problem to be solved. For instance, using a dominance-based EA for problems with more than three objectives may not be a viable choice.
EA的选择:如前所述,需要使用模型管理策略来选择候选解决方案,以便使用真实的目标函数进行评估和训练代理。在已有的在线优化算法中,对EAs的选择问题关注不多。这可以归因于一个假设,即任何EA都可以获得一个很好的近似或接近最优解。然而,在现实中,不同的EAs有不同的优势和局限性,它们应该根据待解决问题的性质来使用。例如,对于超过三个目标的问题使用基于优势的EA可能不是一个可行的选择。
Handling objectives with different latencies: In many real-world multi-objective optimization problems, objectives may have different computation times of different objectives. For instance, in [84], [85], a decision variable is also used as an objective function and the computation time for evaluating such objective functions is negligible compared to other simulation-based objective functions. Some existing and recent studies can be applied to expensive MOPs with different latencies among objective functions. For instance, in [86], a transfer learning was used to build surrogate models among correlated objectives. In an extended work in [87], the authors used transfer learning for sharing information between different parts of the Pareto front. However, they considered the objectives with the same computation time.
A recent work on this topic has been proposed [88] for bi-objective optimization problems, where an algorithm called HK-RVEA was applied to solve problems with objectives of different computation time. Adapting on-line data-driven EAs for handling different latencies among objective functions is one of the important challenges in on-line data-driven optimization.
处理具有不同延迟的目标:在许多真实的多目标优化问题中,目标可能对不同的目标有不同的计算时间。例如,在[84],[85]中,也使用了一个决策变量作为目标函数,与其他基于模拟的目标函数相比,评估该目标函数的计算时间可以忽略不计。现有和近期的一些研究可以应用于目标函数之间具有不同延迟的昂贵MOPs。例如,在[86]中,迁移学习被用来建立相关目标之间的替代模型。在[87]的一项扩展工作中,作者使用转移学习在帕累托目标域的不同部分之间共享信息。但是,他们考虑的目标具有相同的计算时间。
最近关于这个主题的一项工作被提出[88]用于双目标优化问题,其中一种名为HK-RVEA的算法被用于解决具有不同计算时间目标的问题。采用在线数据驱动的EAs来处理不同目标函数之间的延迟是在线数据驱动优化的重要挑战之一。
Termination criterion and performance metric: Last but not the least, a proper stopping or termination criterion and a measure for the performance of the algorithm are also very important when using an on-line optimization algorithm. Where to stop is very important especially for problems with expensive evaluations. For instance, running an algorithm if there is no improvement in the quality of solutions may lead to waste of resources. In the literature, typically conventional performance metrics, e.g., IGD or hypervolume are used to measure the performance of on-line data-driven EAs. These metrics are influenced by several parameters such as the size of the reference set in calculating IGD and may not provide a precise measurement. The effect of parameters on performance metrics has been analyzed in details in [89], [90]. For both performance measure and termination criterion, one should also consider the performance of the surrogate model including the accuracy and uncertainty.
终止标准和性能度量:最后,一个适当的停止或终止标准和一个算法的性能衡量也是非常重要的,当使用在线优化算法。停在哪里是非常重要的,特别是对于昂贵的评估问题。例如,如果解决方案的质量没有改善,运行一个算法可能会导致资源浪费。在文献中,典型的传统性能指标,例如IGD或hypervolume,被用来测量在线数据驱动的EAs的性能。这些度量标准受到一些参数的影响,例如计算IGD时参考集的大小,可能不能提供精确的度量。在[89],[90]中详细分析了参数对性能度量的影响。对于性能度量和终止标准,还应该考虑替代模型的性能,包括准确性和不确定性。
In addition to challenges mentioned above, several other challenges exist related to the characteristics of the problem to be solved. These are dimensions in the objective and decision spaces, handling constraints, and mixed-integer or combinatorial optimization problems. Some on-line optimization algo-rithms, e.g., K-RVEA [12], [91], CSEA [78], and SL-PSO [20] have been proposed to tackle these challenges. However, many real-world on-line data-driven problems are constrained [92]–[97] and / or of mixed-integer decision variables [98]–[104]. Currently, many issues of data-driven EAs for constrained and mixed-integer problems remain open and deserve more attention.
除了上述挑战之外,还存在一些与待解决问题的特点有关的挑战。这些是目标和决策空间的维度,处理约束,混合整数或组合优化问题。一些在线优化算法,如K-RVEA [12], [91], CSEA[78]和SL-PSO[20]被提出来解决这些挑战。然而,许多现实世界的在线数据驱动问题受到约束[92][97]和/或混合整数决策变量[98][104]。目前,约束和混合整数问题的数据驱动EAs的许多问题仍然是开放的,值得更多的关注。
Despite of several challenges, on-line data-driven EAs have the potential of solving optimization problems with different characteristics. The wide applicability of on-line data-driven EAs has demonstrated that on-line data-driven surrogate-assisted evolutionary optimization is of paramount practical importance. Some key promising directions in developing on-line data-driven EAs include 1) using ensemble of surrogate models [16], [49], [50], [93], 2) enhancing the convergence by using a combination of local and global surrogate models [20],[22], [105]–[107], 3) decreasing the computational complexity of the problem to be considered (or problem approximation) by using multifidelity models [31], [32], [34], [108], 4) using fitness inheritance [109], fitness imitation [110] and fitness estimation [19], [111], and 5) using advanced machine learning techniques such as semi-supervised learning [112], [113], active learning [19], [50] and transfer learning [114]–[116].
尽管存在一些挑战,在线数据驱动的EAs有解决不同特征的优化问题的潜力。在线数据驱动的EAs的广泛适用性证明了在线数据驱动的替代辅助进化优化具有极其重要的实际意义。一些关键的有前途的方向在发展中在线数据驱动的EAs包括 1)使用的代理模型[16],[49],[50],[93],2)增强融合利用局部和全局代理模型[20],[22],[105][107],3)降低问题的计算复杂性(或逼近问题)通过使用multi-fidelity模型[31],[32],[34],[108],4)使用适应度继承[109],适应度模仿[110]和适应度估计[19],[111]和5)使用先进的机器学习技术,如半监督学习[112]、[113]、主动学习[19]、[50]和迁移学习[114][116]。
B. Off-line Data-Driven Optimization
Unlike on-line data-driven optimization, no new data can be made available for updating surrogate models during off-line data-driven optimization or for validating the found optimal solutions before they are eventually implemented. Therefore, the main challenges in off-line data-driven optimization may come from the following three aspects.
与在线数据驱动优化不同,在离线数据驱动优化期间,不能提供任何新数据来更新替代模型,或者在最终实现之前验证所找到的最佳解决方案。因此,离线数据驱动优化的主要挑战可能来自以下三个方面。
Lack of data during optimization: One serious challenge is the unavailability of new data during the optimization. Without creating new data for model management during the optimization process, the search ability of off-line data-driven EAs can be limited since surrogate models are built barely based on the data generated off-line. How to effectively use the given data heavily affects the performance of an off-line data-driven EA. As far as we know, several advanced machine learning techniques can be employed to alleviate the limitation. For example, semi-supervised learning [112] can enrich the off-line labelled data by using unlabeled data for training. Data mining techniques [6] can be used to extract patterns from the off-line data to guide the optimization process. In addition, ensemble learning [35] can repeatedly use the training data to enhance the search performance in offline data-driven optimization. Furthermore, transfer optimization techniques [116] including sequential transfer optimization, multi-task optimization, and multi-form optimization are able to reuse knowledge from other similar problems. While sequential transfer optimization learns from historical problems, multi-task optimization [114], [115], [117] simultaneously solves multiple similar problems. Finally, multi-form optimization employs multiple formulations (including multiple fidelity levels of the evaluations [6], [34]) of the original problem to share useful information.
优化期间缺乏数据:一个严重的挑战是在优化期间无法获得新数据。如果在优化过程中不创建新的数据用于模型管理,离线数据驱动的EAs的搜索能力会受到限制,因为代理模型几乎都是基于离线生成的数据建立的。如何有效地使用给定的数据严重影响离线数据驱动EA的性能。据我们所知,一些先进的机器学习技术可以用来缓解这种限制。例如,半监督学习[112]可以利用未标记数据进行训练,丰富离线标记数据。数据挖掘技术[6]可以从离线数据中提取模式来指导优化过程。此外,集成学习[35]可以重复使用训练数据,提高离线数据驱动优化的搜索性能。此外,传输优化技术[116],包括顺序传输优化、多任务优化和多形式优化,能够重用来自其他类似问题的知识。顺序迁移优化是对历史问题的学习,而多任务优化[114]、[115]、[117]同时解决多个类似问题。最后,多形式优化采用原始问题的多个公式(包括评价[6]、[34]的多个保真度)来共享有用信息。
Model reliability: In off-line data-driven optimization, no new data is available to assess the quality of surrogate models, making it very challenging to ensure the reliability. Consequently, the optimization process can be very likely misled. To enhance the reliability of the surrogate models based on off-line data only, multiple heterogeneous or homogeneous surrogate models [49], [118] can be adopted using ensemble learning [119]. Furthermore, cross validation [120], [121] is helpful in accuracy estimation and model selection.
模型可靠性:在离线的数据驱动优化中,没有新的数据可以评估替代模型的质量,这使得确保可靠性非常具有挑战性。因此,优化过程很可能被误导。为了提高仅基于离线数据的替代模型的可靠性,可以采用集成学习方法采用多个异构或同质替代模型[49][118][119]。此外,交叉验证[120],[121]有助于精度估计和模型选择。
Performance verification: The most challenging issue in real-world off-line data-driven optimization is the verification of the solutions found by the optimization algorithm before they are implemented due to the lack of true optimum. In [42], the proposed algorithm is indirectly verified using benchmark problems. Such a verification method is based on an assumption that benchmark problems are similar to the real-world optimization problem to a certain degree. Unfortunately, often little a priori knowledge about real-world optimization problems is available, making it hard to choose the right benchmark problems to reliably test the performance of the algorithm on the real-world problems.
性能验证:现实离线数据驱动优化中由于缺乏真正的最优性,最具挑战性的问题是,优化算法找到的解决方案在实现之前进行验证。在[42]中,利用基准问题间接验证了所提算法。这种验证方法是基于基准问题与现实优化问题在一定程度上相似的假设。不幸的是,通常很少有关于现实世界优化问题的先验知识,这使得很难选择正确的基准问题来可靠地测试算法在现实世界问题上的性能。
V. CONCLUSIONS
The importance of data-driven surrogate-assisted evolutionary optimization cannot be overestimated for EAs to be applied to solve a large class of real-world problems in which no analytical objective functions are available. Unfortunately, this line of research has so far attracted less attention in the evolutionary computation community than it should have due to the following reasons. First, there is a gap between the demands from the industry and the research interests in the academia. Second, there is a lack of dedicated benchmark problems for data-driven optimization that can be made available to researchers and practitioners with few exceptions [34]. Finally, new data-driven surrogate-assisted optimization algorithms are often required to be validated on real-world expensive problems, making it hard for most researchers to perform research in this area due to the lack of access to real-world problems and lack of computational resources.
数据驱动的替代辅助进化优化的重要性不能被高估,EAs被应用于解决没有分析目标函数可用的大量现实问题。不幸的是,到目前为止,由于以下原因,这方面的研究在进化计算界没有引起足够的重视。首先,行业的需求与学术界的研究兴趣存在差距。其次,数据驱动优化缺乏专门的基准问题,研究人员和从业者可以使用,只有少数[34]例外。最后,新的数据驱动的替代辅助优化算法常常需要在现实世界中验证昂贵的问题,这使得大多数研究人员很难进行这方面的研究,因为缺乏对现实世界问题的访问和计算资源的缺乏。
This paper aims to promote research interests in the evolutionary computation community and attract more attention to data-driven evolutionary optimization, simply because data-driven optimization is indispensable for applying EAs to complex real-world problems. Meanwhile, data-driven surrogate-assisted evolutionary optimization provides a unique platform for creating synergies between machine learning, evolutionary computation and data science, potentially leading to the emergence of a new interdisciplinary area, where many research directions should be considered in the future. Firstly, benchmark problems that are extracted from real-world data-driven optimization applications are highly in demand. Secondly, most existing SAEAs deal with on-line direct data-driven optimization problems. Thus, effective new algorithms should be developed for other types of data-driven optimization problems, where the techniques of both machine learning and data science can be helpful. Finally, data-driven EAs for solving real-world optimization problems should be highly encouraged.
本文旨在促进进化计算界的研究兴趣,并吸引更多的关注数据驱动的进化优化,因为数据驱动优化对于将EAs应用于复杂的现实问题是必不可少的。与此同时,数据驱动的替代辅助进化优化为机器学习、进化计算和数据科学之间创造协同作用提供了一个独特的平台,很有可能导致一个新的跨学科领域的出现,这是未来需要考虑的许多研究方向。首先,从实际数据驱动优化应用中提取的基准问题非常受欢迎。其次,现有的SAEAs大多处理在线直接数据驱动优化问题。因此,应该为其他类型的数据驱动优化问题开发有效的新算法,在那里机器学习和数据科学的技术可能是有用的。最后,应该大力鼓励数据驱动的EAs来解决现实世界的优化问题。
2:总结:
1 什么是EAs?
进化算法(evolutionary algorithms):它不是一个具体的算法,而是一个“算法簇”。进化算法的产生的灵感借鉴了大自然中生物的进化操作,它一般包括基因编码,种群初始化,交叉变异算子,经营保留机制等基本操作,简称EAs。
(通俗来讲,EA算法们一般都会有一个fitness function,应该叫适应度函数,首先随机产生父代群落,计算种群的适应度值,然后排序,通过轮盘赌或者其他算法,其实就是模拟适者生存,不适者淘汰的过程,来选择出可以“适者”,然后交叉变异产生后代,反复进化,最后产生的强者就是近似的最优解。)
2 什么叫做数据驱动优化?
数据驱动优化:现实的优化问题中,并不存在一种简单直接的函数,对目标和约束条件的评估只能基于从物理实验、数值模拟或日常生活中收集的数据,这种优化问题可以称为数据驱动优化问题,即:基于从物理实验、数值模拟或日常生活中收集的数据对目标和约束条件的评估称为数据驱动优化。
3 数学优化vs数据驱动进化优化
| 优点 | 缺点 | |
| 数学优化:将问题描述为简单的目标函数和限制条件,通过某种研究方案使目标达到最优的一种方法。 | 速度快,效率高,精度强。 | 对于黑盒问题,无法构造出目标函数,对于复杂问题,可能函数非凸,无法用数学手段达到最优。 |
| 数据驱动优化:基于从物理实验、数值模拟或日常生活中收集的数据对目标和约束条件的评估 | 函数抽象不可描述,或者函数非凸,依旧可解。 | 速度慢,效率低,大规模优化问题难以解决,通常只能达到最优解的近似解 |
大规模优化问题随着GPU的发展,因为其本身并行计算的特点,可以进一步发展有望得到解决
(通常只能达到近似的最优解,因为进化算法在迭代的过程中是伴随着不确定性(例如变异),所以不一定会达到最优解,甚至在有限的时间内,不太可能达到最优解,例如蚁群算法的更新过程,可以看到,最终蚁群并不会沿着直上直下纸横的最优路径走,而是整体上沿着最优方向,局部绕远)
数学优化,比方说,凸优化,线性规划,二次规划,拟牛顿法,梯度下降法
数据驱动优化,比方说遗传算法,蚁群算法。。。
4 数据驱动存在什么问题?
在一些数据驱动的优化问题中,涉及时间与密集型物理实验或数值模拟的评估需要时间很长,导致数据驱动优化的收敛周期长,甚至无法收敛。
(比如说制药问题,他的决策变量为各种原材料,比如锰,CaO,HCl...,他的目标是药效,约束比方说是一瓶药的成本不能高于1000元,药是给人吃的,太贵了那天皇老子也吃不起是不行的,讲到这里,肯定有人会问了,药效的优化问题,怎么评估?就小白鼠呗,所以说,这个问题中,他的评估是很昂贵的,一次评估就是一条生命,而原材料到成品的时间又是很长的,通常不是几分钟可以做出来的。时间成本也消耗不起,所以,现在问题是,数据驱不动了!)
怎么做?
降低成本,使用代理模型。
代理模型:对于许多成本巨大的实际问题,直接对原模型求解不可能,为了简化计算,近似求解原问题,提出的近似模型,如Kriging,ANN,PBFN,支持向量回归等,使用代理模型的EAs,称为SAEAs(surrogate-assisted evolutionary algorithms)。
思考:如果使用代理模型,会出现的问题?
根据天下没有免费的午餐定理,当你获得速度的同时,便会损失精度,代理模型的精度是否足够表示现实模型?
在训练数据有限的情况下,替代模型的近似误差不可避免,这会误导进化搜索。
在构造代理模式的时候,需要关注的问题
5 数据的类型
(比方说制药问题中,他的数据为直接数据,决策变量为锰,CaO,HCl等原材料,目标值为药效,约束值为成本不得高于1000...,门诊部诊断问题中的数据为间接数据,我们无法直接获得患者的决策变量,目标等,但是可以通过分析(计算)就诊记录,将就诊记录中的信息转化为直接数据。)
6 优化方法的类型
离线数据驱动的优化方法(Off-line Data-Driven Optimization Methodologies):在离线数据驱动的EAs中,在优化期间不能主动生成新的数据,对代理管理提出了严峻的挑战。由于不能主动生成新数据,脱机数据驱动的EAs关注于基于给定数据构建代理模型,以探索搜索空间。在这种情况下,代理管理策略严重依赖于可用数据的质量和数量。
在线数据驱动优化方法(On-line Data-Driven Optimization Methodologies)在线数据驱动的EAs可以提供更多的数据来管理替代模型。因此,在线数据驱动的EAs比离线数据驱动的EAs更灵活,这比离线数据驱动的EAs提供了更多的机会来提高算法的性能。
非理想质量的数据(Data with non-ideal quality) 真实世界的数据可以是不完整的,不平衡的,或有噪声的。因此,代理的构建必须考虑到这些挑战,即使如此,所产生的代理依旧会受到很大的近似误差,可能会误导进化的搜索。
大数据(Big data):在离线数据驱动优化中,数据量可能非常大,这导致基于数据进行数据处理和适应度计算的计算成本非常高。建立代理模型的计算成本也会随着训练数据量的增加而急剧增加。
小数据(Small data):相对于大数据,由于收集数据的时间和资源有限,可用的数据量可能极小。数据的缺乏通常归因于复杂系统的数值模拟计算非常密集,或物理实验非常昂贵。小数据带来的一个直接挑战是代理的质量差,特别是对于脱机数据驱动优化,在优化期间不能生成新数据。
解决办法?
数据预处理:对于质量不理想的数据,需要进行预处理。然后再对其进行训练代理,以提高数据驱动EAs的性能。
(通过数据预处理,可以把非理想质量的数据较理想化,比如通过箱线图,筛选出数据中的离群点,均值法或者回归法填补空缺数据,回归平滑消除噪声,对于数据残缺很大,可以直接删除该例数据之类的。。。)
2)数据挖掘:当数据驱动的EAs涉及大数据时,计算成本可能难以承受。由于大数据通常具有冗余,现有的数据挖掘技术可以用于捕获数据中的主要成分,数据驱动的EA是基于获得模式(obtained patterns),而不是原始数据,以减少计算成本。
(比如40000个数据,可以用聚类技术从数据中挖掘成分,很多数据几乎相近的,比如175cm,175斤和170cm,170斤的两个数据,我们可以将其聚为一个数据族,最终,可以把40000个数据聚类为100个族,数据驱动对这100个族进行优化,就是所谓的基于获得模型)
3)人工数据合成:在数据量较小且不允许生成新数据的情况下,获取高质量的代理模型极具挑战性。为了解决这个问题,可以在离线下合成人工数据。
(比如控制其他变量,1g锰响应的药效为0.9,1.1颗锰相应药效为0.92,那是不是可以预测1.05g锰药效为0.91?)
低阶多项式回归:一般时间序列中的局部趋势可以由低阶多项式回归很好的逼近,使用低阶多项式模型可以较好的对局部变化的趋势进行拟合。
(为什么不用高阶?)
因为我们考虑的范围是在一个局部,对于实际问题,任何一个实际问题的局部变化,都可以近似的看做是线性的,所以我们可以在较小的局部范围内,使用低阶线性来得到一个较好的拟合结果。
(为什么只需要考虑局部而不用考虑全局?)
假设对于这样一个问题,如果考虑全局最优,那么任何一个低阶多项式都无法拟合这个函数,但是直觉告诉我们,最优解应该在红色区域,当我们考虑红色区域的时候,我们必须认识到,这些剧烈的抖动是由于噪声构成的,显然,如果多项式的项数少于样本点的个数,我们就可以得到一个平滑的模拟曲线,这样,我们就可以得到一个平滑噪声后的曲线,如蓝色所示。
为了更好的说明问题,我盗了更加真实的数据以及对应的低阶多项式回归曲线 ,如下图所示
通常,离线的数据驱动优化更需要关注已有数据本身的性质,为了充分利用数据,可以考虑集成学习思想,使用多个模型集成,在集成学习的时候,需要兼顾模型的准确性和多样性,才能发挥集成学习的优势
准确性:个体学习器不能太差,要有一定的准确度(即不能有一个太短的短板)
多样性:个体学习器之间的输出要具有差异性(各有所长的意思,不能所有的学习器的优点都是一样的)
而在线的数据驱动优化则更应该关注什么时候优化停止,以及对新生成的数据做如何处理 根据对新生成数据的处理方式不同,可以分为基于个体策略(individual-based)和基于世代(generation-based)的策略。
基于世代的策略对生成的新数据的采样频率进行调整,而基于个体的策略则选择每代抽取一部分个体进行采样。
根据个体的不同,将样本分为了 有希望的样本和不确定的样本,基于个体的策略所做的,正是平衡这两者之间的关系。
有希望的样本位于代理模型的最优位置周围,一旦对有希望的解决方案进行采样,替代模型在有希望区域的准确性就会提高
不确定样本位于代理模型的搜索空间中可能会有一个巨大的逼近误差而EA尚未完全探索的区域。
例如,当随机生成样本的范围再橙色区域时,模型认为向右将会是有希望的点,而左边由于误差巨大导致模型不太可能探索该区域,因而忽略了左边可能的情况,对于这些不确定的样本,也应该加以关注,目前,更多的做法是平衡两者之间的关系,例如预期改进( expected improvement ExI),概率改进(probability of improvement PoI) 置信下限( lower confidence bound LCB)。
假设这样一个问题,如图搜索空间,问题为从A到B的最下成本路径,AB是次优解,AC→B是最优解,那么EA将会发现有希望的解集中在灰色趋于,如果仅仅考虑有希望的解,那么将永远无法发现最优解AC,因为该区域附近(两条蓝色路径之间的区域)被认为是高逼近损失的。
(假如C是一个时空隧道,从C可以直接传送到B,而C周围任何一点都没有时空隧道)
综上。